三角恒等变换作用解析

◇ 河北 韩立强

三角恒等变换作用解析

◇ 河北 韩立强

三角恒等变换是三角函数部分的重点内容,在解决三角函数图象、性质等相关问题时具有重要的作用,下面举例分析.

1 求三角函数的相关性质

利用三角变换将一个复杂的三角函数式转化为只含一个角、一个三角函数的形式,进而判定相关的性质是解决有关问题的重要思路和有效方法.

例1若函数y＝sin2x＋acos2x的图象关于直线x＝—对称,则a＝( ).

2 化简求值

利用三角恒等变换可以达到化简和求值的目的,灵活运用三角公式是关键,尤其是掌握角变换的基本技能.角的变换是沟通未知与已知的桥梁,正确的变换方向可以达到化未知为已知的目的.常见的化角技巧有拆角和凑角.

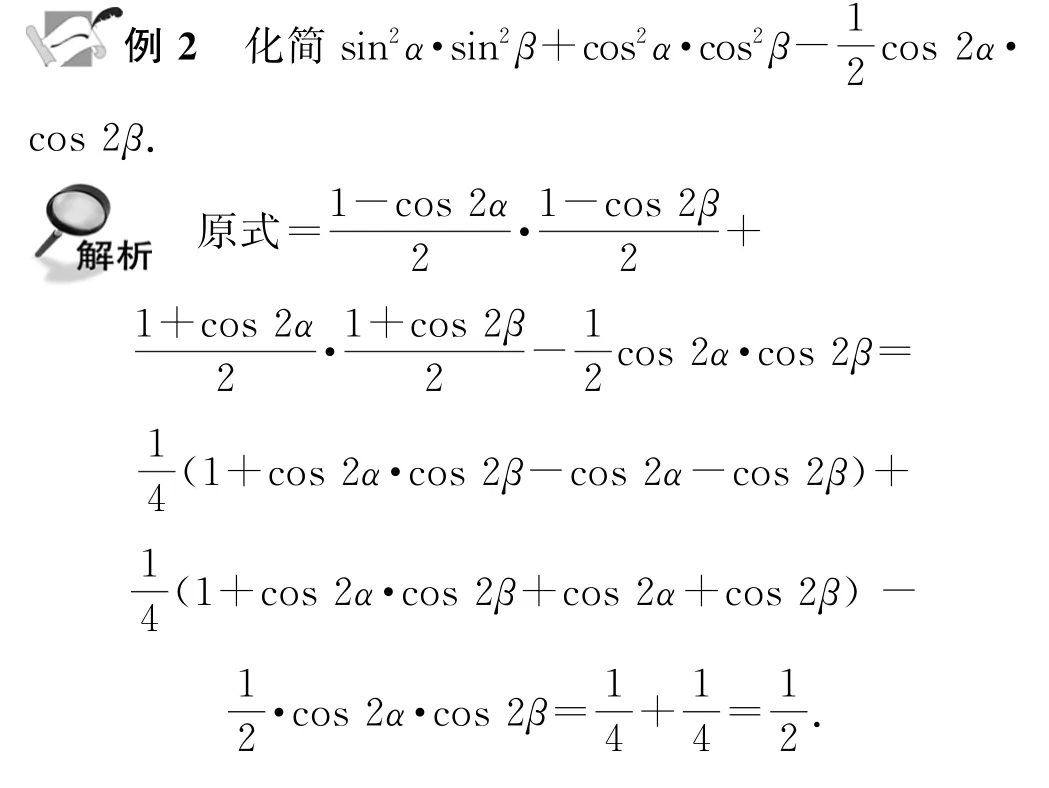
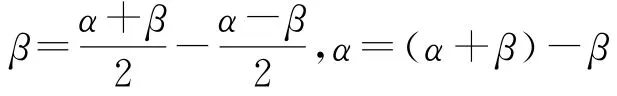
3 解决与平面向量有关的问题

三角函数问题常常与平面向量知识结合考查,通常以平面向量知识为背景,考查利用三角恒等变换解决相关问题.

例4如图1放置的边长为1的正方形ABCD的顶点A、D分别在x、y轴正半轴上(含原点)上滑动,则的最大值是___________________.

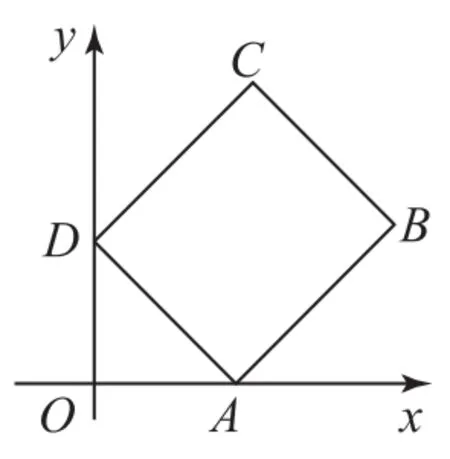
图1

解析

设∠OAD＝θ,则OA＝AD·cosθ＝cosθ,点B的坐标为(cosθ＋cos(90°－θ),sin(90°－θ)),即B(cosθ＋sinθ,cosθ).同理可求得C(sinθ,sinθ＋cosθ).所以

遇到平面向量与三角函数相结合的题目,设角引入坐标是解题的关键,所以在研究此类题时应该想到设角来表示点的坐标.

(作者单位:河北省滦县第二中学)