基于河网水动力学模型的珠江三角洲排涝调度设计

杜伟华，赵宇坤，贺顺德

（1.山东黄河河务局，山东济南250011；2.黄河勘测规划设计有限公司，河南郑州450003）

基于河网水动力学模型的珠江三角洲排涝调度设计

杜伟华1，赵宇坤1，贺顺德2

（1.山东黄河河务局，山东济南250011；2.黄河勘测规划设计有限公司，河南郑州450003）

基于一维非恒定流的圣维南方程组，在节点水量严格平衡的基础上，结合防洪防潮排涝调度设计，对河网水动力学模型的闸泵入出流计算和河网节点设计进行优化。针对广州市番禺区蕉东联围排涝区的外江水闸和河道整治项目，探讨了河网概化方法、边界条件的确定和模型的输出。

珠江三角洲；水动力学模型；河网概化；排涝调度

0 引言

近年来，水动力学模型在河道洪水模拟、城市管网排水设计等方面得到了很好的应用。珠江三角洲位于珠江下游的平原地区，地势低洼平坦，河网密布，是珠江水系内陆河流的入海河口。受外江洪潮水位顶托，该区河道泄水不畅，洪涝灾害频繁。由于珠江三角洲地区河网纵横交错，建筑物众多，水流运动十分复杂，用水动力学模型对河网水流运动情况进行数值模拟，建立适用于珠江三角洲地区河网水动力学模型，为地区防洪、防潮、排涝等规划设计提供技术依据尤为重要。

广州市番禺区地处珠江三角洲中心，东临狮子洋，与东莞市隔江相望；西及西南以陈村水道和洪奇沥为界，与佛山市南海区、顺德区及中山市相邻；北隔沥滘水道，与广州市海珠区相接；南及东南与广州南沙开发区相邻。番禺区番禺区蕉东联围属于典型的平原感潮河网地区，为了配合《广州市番禺区外江水闸及河道整治工程》的顺利完成，笔者建立了珠江三角洲地区河网水动力学模型，以期为广州市番禺区外江水闸和河道整治工程的设计提供依据。

1 河网水动力学模型的基本原理和优化

1.1 基本方程组

对于平底、棱柱形明渠中的非恒定流，根据一维非恒定流动基本方程组—圣维南方程组求解，如式（1）和式（2）所示［1］。

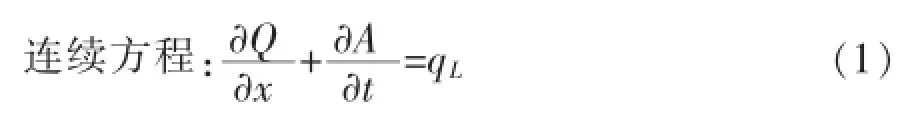
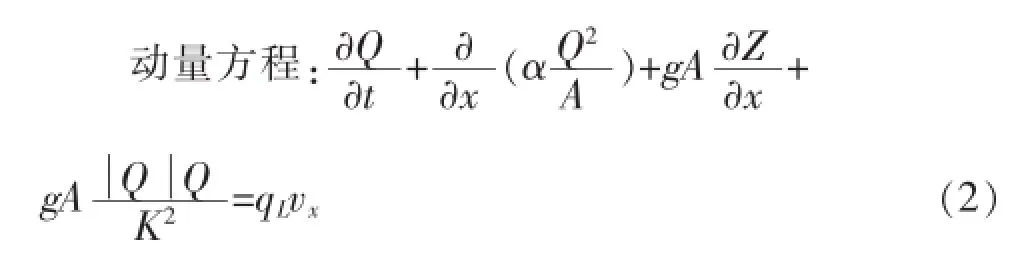
式中：x为距离，m；t为时间，s；A为过水断面面积，m2；Q为断面流量，m3／s；Z为断面水位，m；α为动量修正系数；K为流量模数；qL为单宽旁侧入流量，m2／s，入流为正，出流为负；vx为入流沿水流方向的速度，m／s。

在水流运动模拟计算中，规划的河道断面可以按式（3）优化成梯形断面［2］。

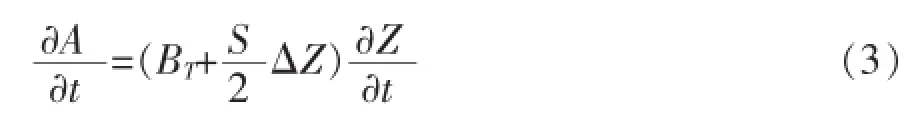
式中：S为两侧边坡之和；ΔZ为Δt时段内水位增量，m；BT为梯形断面的开口宽，m。

由式（4）可知，δ*总是大于零的，且水位变幅越大，δ*值越大。因此，对于潮水河道，计算历时较长时，如果忽略这一项会引起水量平衡的误差。以水位和流量为变量的平底棱柱体河道水流非恒定运动的基本方程组如式（5）和式（6）所示。

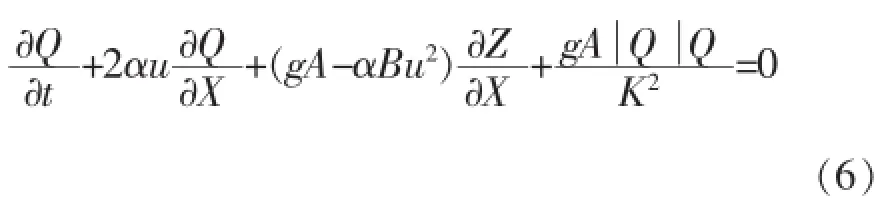
1.2 闸门及运行方式模拟［3］

在水流模拟中，不仅要正确地模拟水闸工程的规模、位置，而且还要模拟水闸的控制运行方式。在河网概化中，每条河道两端均设有节点，河道与河道的连接均通过节点，水闸的上、下游也设有节点。即，每个控制建筑物均介于上、下节点之间。堰闸的概化模型如图1所示。概化模型与河道不同之处是：（1）两节点之间的距离可以忽略不计；（2）节点之间水位差与流量之间的关系取决于堰流公式及运行方式。

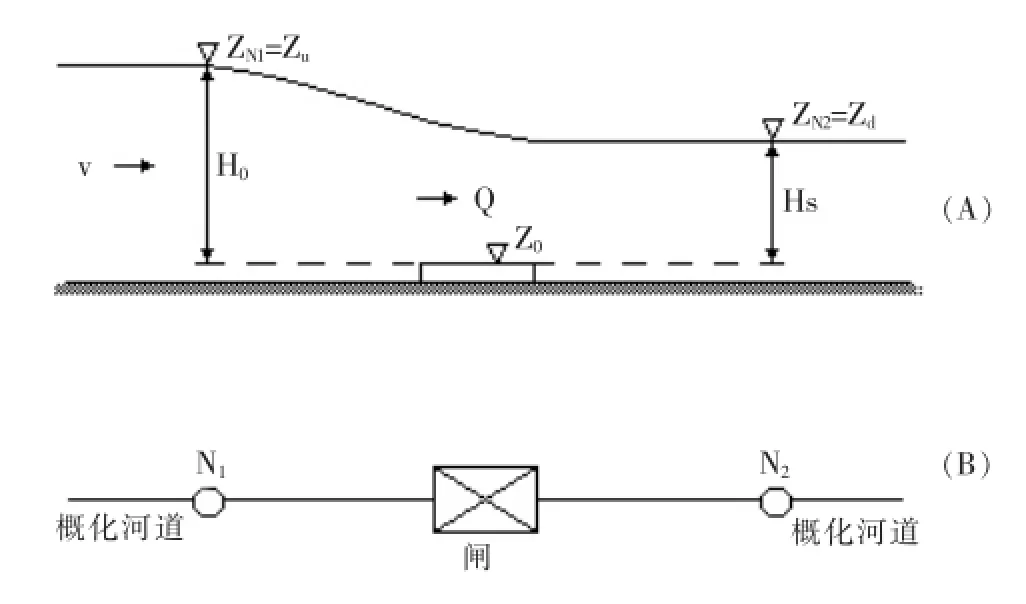
图1 堰闸概化示意图Fig.1 W eir sluice sim p lified method

在闸门开启情况下，过闸流量Q可按式（7）和式（8）所示的宽顶堰公式进行计算。

式中：Q为过闸流量，m3／s；m为自由出流系数；φ为淹没出流系数，一般取1.0～1.18之间；B为闸门开启总宽度，m；Z0为闸底高程，m；Zu为闸上游水位，m；Zd为闸下游水位，m。对于已建控制建筑物最好根据实测过闸流量来确定系数m和φ值。

为了计算方便及两种出流之间的衔接连续，将自由出流公式与淹没出流公式统一成式（9）。

1.3 简单河网方程［4］

简单河网示意图如图2所示。

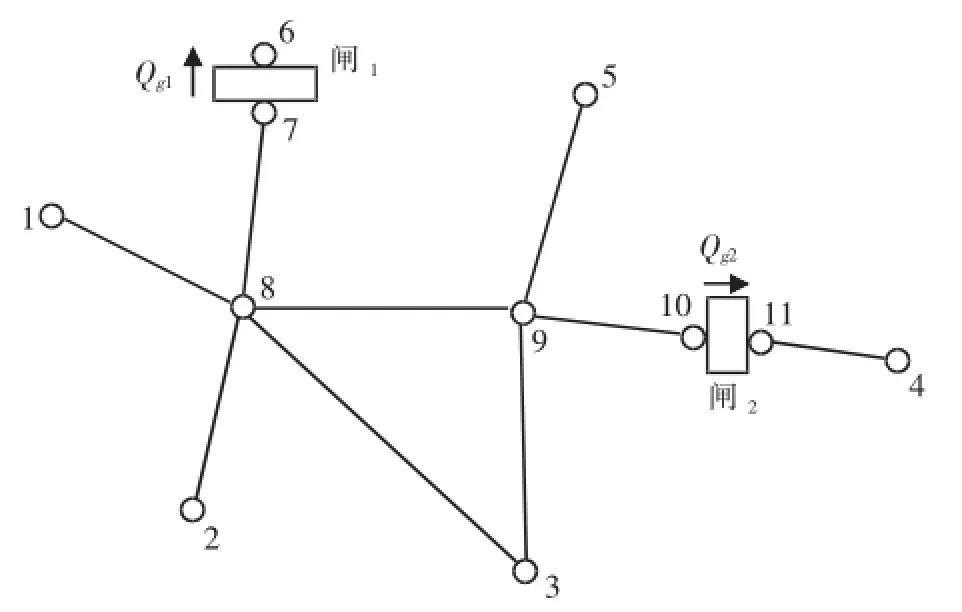
图2 河网示意图Fig.2 River network

在图2中，有9条河流，11个节点，2个闸。其中，节点4、5、6为水位边界点，其水位为已知值。其他节点水位和水闸的过闸流量可用下列方程组计算。

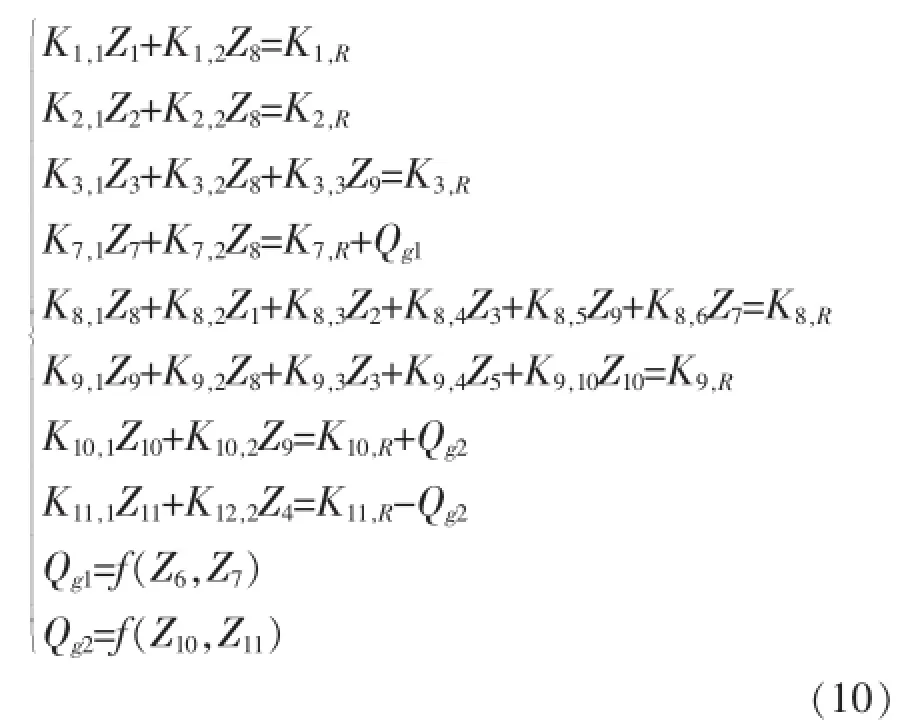
式中：Z1，Z2，…，Z11为节点水位；Qg1、Qg2分别为闸1与闸2的过闸流量。

由方程组（10）可知，节点水量平衡方程式是线性的，过闸流量方程式是非线性的。方程组的求解采用迭代法。

2 河网水动力学模型的应用

2.1 河网概化

在采用河网水动力学模型计算河道水面线，并计算水闸和泵站规模时，需要根据区域地形特征和城市建设规划情况，以及现状和规划的排涝工程布置特点，绘制河网概化拓扑图。本设计绘制拓扑图时，河段、泵站、闸门分别编号（其中，泵站和闸门由3个节点表示，中间节点表示闸门编号，两侧节点表示入流和出流）。然后，根据河网概化河段及节点情况，并依据河段的汇流特点，将整个蕉东联围排涝区划分为较小的分区。分区时，根据河段长度，并考虑河段所在的汇水面积和地形条件，按河段数将蕉东联围排涝区划分为59个排涝小区。蕉东联围河网概化拓扑图如图3所示。

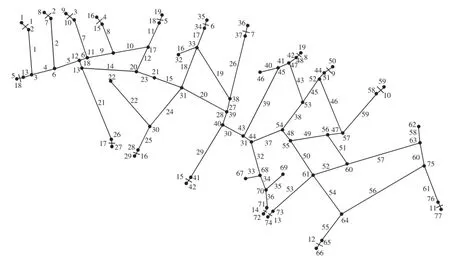
图3 蕉东联围河网概化拓扑图Fig.3 Jiaodong lianwei river network topology map

2.2 边界条件［5］

（1）河道断面。根据蕉东联围排涝区的水系特点、河网特性及规划的河道断面进行河道断面概化。概化时，断面间距一般取为500～1 000m。

（2）设计洪涝水。根据河网概化河段及节点情况、河段的汇流特点，将整个蕉东联围排涝区划分为59个排涝小区，并将整个联围的设计洪水成果分配到每个汇水小区。但是，最终各小区设计洪水成果以整个蕉东联围排涝区的设计洪水成果作为控制。

（3）设计外江潮位过程。设计外江潮位过程同样采用多年平均高潮位过程和多年平均最高潮位过程2种。按照设计的外江潮位过程分别对自排水闸规模和抽排情况下的泵站规模进行复核，并确定自排和抽排情况下的水闸泵站联合运用方式。

（4）河道控制水位。河道起调水位确定为0.2m，最高控制水位采用1.0m。

（5）河道糙率。蕉东联围排涝区河道糙率缺乏实测资料，根据各河流的现状以及规划断面形式，初步拟定河道的综合糙率为0.027。

（6）泵闸联合运用方式。自排情况下，外江水位较低。首先开启闸门，当外江水位高于闸门前水位时，关闸。外江水位回落，当低于闸门前水位时，开闸抢排，直至闸前水位距河道常水位0.2m时，关闸，维持常水位。抽排情况下，外江水位较高，此时关闭闸门，闸内水位抬升至0.2m时，开启泵站抽排，直到外江水位开始回落，并低于闸内水位时，开闸抢排，直至闸前水位距河道常水位0.2m后，关闸，维持常水位。

2.3 模型输出

模型输出的成果为河道水面线、河道内各节点的水位历时变化过程线、各节点的流量及流向、各闸的排水流量过程、泵站的抽排流量过程、外江水位的变化过程等，因篇幅所限，本文不再详列。根据不同边界条件的模拟结果，以河道水面线不超过河道最高控制水位为原则，可以通过试算综合分析该排涝区的河道整治规模、泵站抽排规模和水闸排水规模。由于蕉东联围内河网交错，相互串流，所以排涝模式为整体排涝。在排涝设计时，需要综合考虑河道的调蓄作用和泵站的抽排作用，以及外江水闸的自排作用，使得排涝模式更合理。

3 结语

通过建立的河网水动力学模型对珠江三角洲地区水流状态的数值模拟，经过不同边界条件的组合和不同排涝方案的优化，可以提供满足该地区排涝要求的河道整治规模、水闸泵站设计规模以及设计的水闸泵站防洪排涝运用方式。同时，该模型也可以为平原感潮地区的防洪、防潮、排涝调度提供技术支撑。

参考文献：

［1］付典龙，傅春.一维圣维南方程组的特征线法［J］.南昌大学学报：工科版，2006，28（4）：386－389.

［2］徐祖信，卢士强.平原感潮河网水动力模型研究［J］.水动力学研究与进展，2003，18（2）：176－181.

［3］严文武，邹长国.水动力模型在平原感潮河网地区的研究与应用［J］.浙江水利科技，2007（4）：8－10.

［4］吕满英，江洧，詹杰民.河网节点水流连接条件处理方法研究［J］.人民黄河，2007，29（3）：31－33.

［5］李毓湘，逄勇.珠江三角洲地区河网水动力学模型研究［J］.水动力学研究与进展：A辑，2001，16（2）：143－155.

[责任编辑 杨明庆]

Design of T he Pearl River Delta Drainage Regulation Based on Hydrodynam ics M odel for River Network

DU Wei－hua1，ZHAO Yu－kun1，HE Shun－de2
（1.Shandong Yellow River Bureau，Jinan 250011，Shandong，China；2.Yellow River Engineering Consulting Co.Ltd.，Zhengzhou 450003，Henan，China）

Based on the Saint－Venant equations of one－dimensional unsteady flow，on the basis of nodeflux strict balanced，and combin g with flood and moist control and drainage regulation design，it optimizes pump works in－out flow calculation and node design of hydrodynamics model for river networks.It discusses the river network simplified method，boundary conditions and the output of the model in view of the outer river brake and channel improvement project of jiaodong lianwei drainage area in Panyu district of Guangzhou city.

The Pearl River Delta；hydrodynamics model；river networks simplified method；drainage regulation

TV13

A

10.13681／j.cnki.cn41－1282／tv.2016.04.001

2016-03-23

杜伟华（1975-），男，山东齐河人，高级工程师，硕士，研究方向为水利工程建设与管理。