湖北省地类表面积栅格与矢量叠加统计算法探究

高 昂，何青松

(1. 黄冈中学，湖北 黄州 438000；2. 武汉大学 资源与环境科学学院，湖北 武汉 430079)

湖北省地类表面积栅格与矢量叠加统计算法探究

高 昂1，何青松2

(1. 黄冈中学，湖北 黄州 438000；2. 武汉大学 资源与环境科学学院，湖北 武汉 430079)

本文通过DEM生成表面积栅格，然后在表面积栅格的基础上提出了一种顾及多边形边界精确裁剪的栅格与矢量叠加统计算法CVOA。与传统的做法相比，在处理时间上极大缩短，能够满足大规模的工程应用。本文以湖北省具有典型平原地貌特征的仙桃市，丘陵地貌的罗田县以及高山地貌的神农架林区为研究区，计算各个研究区内的各个地类的表面积取得了很好的效果。

投影平面面积；地表表面面积；DEM；边界；工程应用；地貌特征

地表表面面积是指结合地形条件的地球表面的面积。在地理信息技术领域，对地球进行建模时通常将地球简化为一个标准的椭球体，而不考虑地球表面实际的起伏情况。在资源调查中，基于椭球面积而不是表面积测算得到的面积常常被用来评价生物资源、土地资源规模、生态服务价值等[1-4]。然而不论是人类还是自然界中的其他各种生物都生活在有地形起伏的地形上[5-6]。由于地球表面高地起伏较大，导致地表表面面积与椭球面积会在山区和丘陵地区会存在较大差异。因此，仅仅以地物的椭球面积来表示地物的面积是不能满足资源调查(国土调查、林业调查)等实际应用的需要[7]。在生物地理学领域，地形通常被认为通过异质性和分离性显著的增加了生物多样性[8-9]；文献[10]在估算水稻种植面积时注意到了水稻种植易受地表起伏影响的特点,在分析时加入了坡度信息[10]；在风化作用中，地表表面积被认为是至关重要的决定因素[11]。

随着GIS技术以及Digital Elevation Models(DEM)模型发展，衍生出越来越多的基于DEM求算地表表面积的算法[12-16]。然而这些算法多只存在于理论或小尺度的应用上。基于DEM的统计单元表面面积统计主要包括以下4种：(1)利用DEM构建区域的不规则三角网(TIN)[17-18]，在此基础上叠加需要计算表面面积的矢量多边形，由不规则三角网与多边形的叠加计算得到各多边形的表面面积[19-20]； (2)直接基于数字高程模型数据构建规则三角网，在此基础上叠加需要计算表面面积的矢量多边形，由规则三角网与多边形的空间位置关系，汇总落入多边形内的空间三角形的面积得到各多边形的表面面积[16]；(3)基于相邻的4个DEM栅格像元，利用积分公式推算出由4个相邻像元构成的区域的曲面面积，进而依据该曲面与多边形的空间位置关系，汇总落入多边形内的曲面面积，从而得到多边形的表面面积[21]。(4)利用DEM上3*3的像元窗口构建8个空间三角形，计算3*3区域内的中心像元区域的表面面积，进而利用栅格像元与多边形进行叠加，汇总落入多边形内栅格像元值作为多边形的表面面积[7]。然而上述相关算法模型都没有经过大规模工程应用的检验，且回避了怎样计算目标区域边界附近面积的问题。

中国幅员广阔，椭球投影面积就约有960万平方千米，且中国是个多山地地貌的国家，山地面积占到全国总面积的2/3以上[22]。国务院第一次全国地理国情普查领导小组办公室规定县级行政单元各个用地类型的表面积统计是国家的一项关键的基本国情统计指标。 因此如何快速且准确的计算出各个县级行政单元各个地类的表面面积对科研人员提出了巨大的挑战。本文正是作者及其合作者在思考解决这个工程级应用问题时的一些思考和实验尝试。本文主要解决两个问题：(1)在DEM基础上如何高效率、高精度的获取表面积栅格文件；(2)栅格与矢量叠加统计时如何在顾及矢量多边形边界基础高效率的计算多边形的表面积。

1 数据及方法

1.1 研究区及使用数据

仙桃市:位于湖北中南部，江汉平原腹地。地势平坦，起伏甚微，是湖北省江汉平原中心城市, 面积2 538平方千米,见图1(a)。

罗田县：位于湖北省东北部、大别山南麓，地处东经115°06′至115°46′，北纬30°35′至31°16′之间。境内多200米以下小山丘，丘陵广布。面积2 145平方千米，见图1(b)。

神农架林区：位于湖北省西部。境内多高山，以神农顶最高，高程为3 105.4米，是华中地区最高点，呈现典型的山地地貌。面积3 253平方千米，见图1(c)。

本文使用的数据来自于全国第二次土地利用调查数据中用地类型数据以及研究区的30m分辨率的DEM。

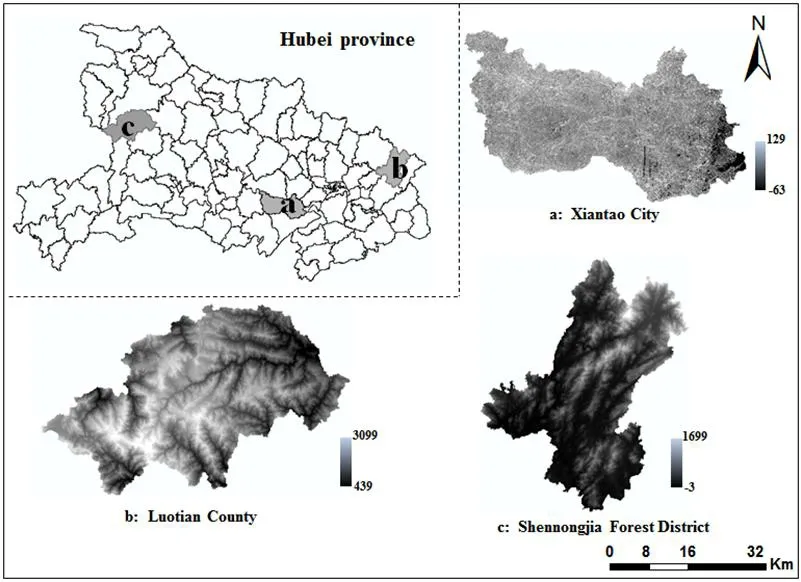
图1 研究区

1.2 方法

1.2.1 基于DEM生成表面积栅格

(1)坐标之间的转换。为了在三维空间中精确的描述地球表面有个点的位置，通常需要借助某种特定的坐标系统得以完成。常用的坐标系统主要可以分为3种：1)大地坐标系，2)平面投影坐标系， 3)空间直角坐标系。在大地坐标系下，各个点的位置是直接基于经纬度坐标进行表示，点的位置是精确、没有偏移和变形的；在投影坐标系下，各点的位置是一种平面位置，依据投影方法的不同，投影前后的几何形状可能在角度、长度和面积等方面都产生一定的变形和偏移；空间直角坐标系是一种三维坐标系，各点的位置由三维坐标系下的真实的X,Y,Z坐标描述，没有因为投影带来的变化。三种坐标系中，大地坐标系和空间直角坐标系表示的点位和几何形状是没有变形的，而基于平面直角坐标系的点位和几何形状是有变形或偏移的。

在计算三角形面积时，为了避免平面投影产生的变形，需要以空间直角坐标系作为三角形顶点坐标存储单位。在大地坐标系下任意一点(B,L,H)可以采用以下计算公式转换为空间直角坐标系下的(X,Y,Z)，计算公式如下：

(1)

(2)

(3)

式中：B,L,H分别表示某点的纬度、经度和高程值；X,Y,Z分别表示该点在三维空间直角坐标系中的坐标值；Cos(B)为纬度的余弦值，Sin(B)是纬度的正弦值，Sin(L)是经度的正弦值，Cos(L)是经度的余弦值。e2为地球椭球体的第一偏心率的平方，作为地球椭球体的已知常数输入。N的计算公式如公式(4)：

(4)

式中：a为地球椭球体的长半轴。a和e2均为常数，可在地球参考椭球体的定义中查找得到。

(2)地表表面面积计算原理。计算地表表面面积的前提是对地表表面进行数值模拟和逼近。数字高程模型DEM，通常利用栅格图像来表示地球表面高程(也称为“海拔”)的高低起伏情况。DEM以离散的、规则的网格对地表进行了模拟[7]。然而，地表是一个连续的表面，基于DEM无法直接得到连续的表面。因此，在计算地表表面时，通常基于DEM上离散的栅格点构建相互连接的三角网(在空间直角坐标系中，任意3个点都能保证在同一个平面上，而3个以上的点无法保证在同一个平面上，也无法计算面积)。以相互连接的多个三角形构成的三角网来逼近地表真实的连续表面[19]。给定空间三角形顶点的A,B，C及其坐标(XA,YA,ZA)、(XB,YB,ZB)和(XC,YC,ZC)，其面积S可利用海伦公式(5)得出：

(5)

式中：p=(a+b+c)/2。a,b,c分别表示三角形的边长。空间三角形的边长可以采用下式公式(6)计算得到：

(6)

式中：lij表示任意两点i,j的三维空间距离，(xi,yi,zi)和(xj,yj,zj)分别表示两点的三维坐标。

设DEM采用大地坐标系进行存储，栅格像元的行数为M,列数为N，栅格分辨率为C。则生成表面积栅格的具体步骤如下： 首先创建一个(M-1)*2行、(N-1)*2列的空的栅格文件，栅格文件中各栅格像元的值默认为0。设原始DEM的起始点经纬度坐标为(B1,L1)，则新栅格文件的起始点经纬度坐标为(B1+C,L1+C)。

接着按行遍历DEM栅格，按照以下方法构建规则三角形并计算栅格像元区域的表面面积：

(1)设i表示当前遍历的行号、j表示当前遍历的列号，i初始值为2，j初始值为2,从DEM的第二行第二列开始遍历。则当前遍历的栅格像元行列坐标为(i,j)。按照图2中的方法，分别获得行列号为(i-1,j-1),(i,j-1)和(i-1,j)栅格像元点，构成相邻的4个点并分别进行编号。当前点为3号点。

(2)由步骤(1)相邻的4个点可在平面上得到一个四边形。按照图3的示意图，内插出四边形四条边的中点高程值和对角线交点的高程值。图3中，任意一条边的中点，如6、7、8、9号点的高程值和经纬度坐标由其边上两点的高程值的平均值计算得到。

(3)由步骤(1)和(2)可以得到空间上相邻的8个空间三角形，并按照图3的方式进行编号：I、II、III、IV、V、VI、VII、VIII。

(4)利用海伦公式分别计算8个空间三角形的面积。

(5)由三角形I、II可得到一个新的平面四边形编号为(一)，三角形III、IV可得到一个新的平面四边形编号为(二)；三角形V、VI可得到一个新的平面四边形编号为(三)；三角形VII、VIII可得到一个新的平面四边形编号为(四)，如图4所示。

(6)根据8个空间三角形与4个新的四边形的组成关系，分别汇总三角形的面积得到4个新的四边形的面积，分别记为S1、S2、S3、S4。

(7)将4个新的四边形的面积写入到新的栅格文件的对应行列号中。其中，S1写入新栅格的行列坐标(2i-1,2j-1)，S2写入新栅格的行列坐标(2i-1,2j)，S3写入新栅格的行列坐标(2i,2j)，S4写入新栅格的行列坐标(2i,2j-1)。重复执行步骤(1)～(7)直至遍历完所有的行列。

由图4可知，新的栅格文件的空间分辨率是原来的一半，空间精度更高。新栅格文件中，栅格像元的值表示了该区像元占据空间区域的地表表面面积，该栅格文件定义为数字地表面积模型，标记为SAM。

图2 相邻4个DEM栅格点示意图

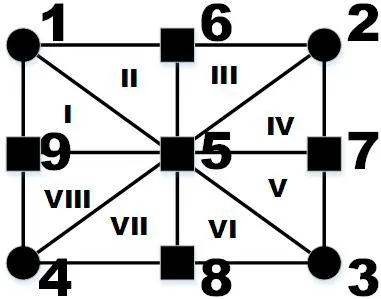
图3 DEM内插原理示意图

图4 四边形构建原理示意图

1.2.2 矢量与栅格叠加运算

栅格与矢量空间叠加时(见图5)，只有栅格像元的中心点落在多边形内时，该像元被认为落在多边形内，否则不在多边形内。如图5所示，一个矩形表示一个栅格像元，矩形内的圆点表示栅格像元的中心点。在基于栅格做空间运算时，通常以栅格像元的中心点代替整个栅格以简化计算提高计算效率。图5(a)中的多边形的面积在ArcGIS中统计的值为图5(b)中灰色填充栅格值的求和。不难发现这个值与该多边形的真实面积存在误差。当一种地类由很多这样的多边形构成时累积的误差更大。ArcGIS这种矢量栅格叠加统计方式对于摸清地类表面积的大概十分有用，然后却无法精确的掌握类型的表面积。很明显该方法的精度与DEM的空间分辨率有关，DEM分辨率越低,面积统计精度也越低。这种计算方法在处理比较小的图斑的时候会对结果产生较大的影响。

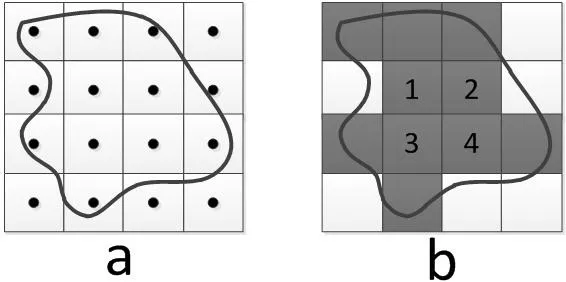
图5 矢量栅格叠加统计示意图

对于只有部分覆盖的栅格，想直接精确求出多边形与该栅格相交部分的表面面积是不可能的。但是通过求该相交部分的平面面积与该栅格的平面面积得到一个比值，以该比值作为该相交部分应该分配到的当前栅格值的比例是个可行的办法，他能最大程度的保证表面积的精确程度。因此此时的问题转到了如何快速求多边形与所有相交栅格相交部分的平面面积。矢量数据中的多边形由各个弧段组成，弧段则由两点连线构成。因此矢量多边形可以看成是由多个点连线构成。任意多边形的平面面积可由任意一点与多边形上依次两点连线构成的三角形矢量面积求和得出。而矢量面积等于三角形两边矢量的叉乘[23]。假设构成多边形P的点坐标依次为(x1,y1),(x2,y2),…,(xm,ym)(图6)。则该多边形P的面积可由公式(7)计算：

(7)

式中：Sp为多边形P的面积，为以P0、Pk、Pk+1为顶点构成的三角形的面积。

使用该公式计算的面积顶点坐标顺序为逆时针时候为正，顺时针时为负。但是无论正负，最终的结果取绝对值即为该多边形的面积。

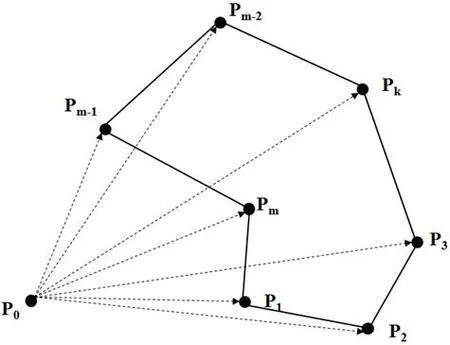
图6 矢量面积法示意图

计算速度是栅格与矢量叠加统计时需要解决的一个重要问题。在ArcGIS实现中通过“扫面线算法(Sweep Line Algorithm)，逐个像元进行扫描判断栅格与多边形的交点。当像元数量以及多边形的数量较多的情况下算法时间过长，不适合大规模的工程应用。不难发现尽可能的减少空间操作次数是提高统计速度的一个有效捷径。因此本文作者提出了顾及边界精确裁剪的栅格与矢量叠加统计算法 (CVOA)，它通过对表面积栅格进行整行的边框提取构建矩形，利用该矩形裁切多边形，得到多边形与矩形的相交区域。我们已经知道矢量多边形其实是由点构成，通过点的坐标就可以知道点所在栅格中的具体位置。将一个栅格内的所有点围成的多边形按照公式7求出平面面积，再将该面积与该栅格的平面面积得到一个比值，以该比值作为该相交部分应该分配到的当前栅格表面积值的比例就可以知道当前相交部分的表面面积。

2 结果

统计的表面积结果如表1所示。其中表头中Area 表示平面投影面积；ArcGIS_SA 表示用ArcGIS统计得到的表面积；CVOA_SA表示CVOA算法计算得到的表面积； D1=ArcGIS_SA-Area；D2=CVOA_SA-Area；D3=CVOA_SA-ArcGIS_SA。

3 讨论

经过上述三个县为例进行的算法实验，可以明显看出本文提出的栅格与矢量叠加统计算法在统计结果和时间效率上与传统方法有明显的不同。

3.1 表面积栅格生成

本文提出的表面积栅格生成方法主要优势在于：(1)直接基于大地坐标系下的DEM进行计算，避免了构建不规则三角网时需要进行平面投影和DEM栅格点抽稀的精度损失；(2)避免了矢量多边形和规则三角网(也是矢量)叠加时产生的巨大计算量，效率优势明显。(3)计算简单，计算量小，无需复杂的积分运算，适合大规模计算任务的求解。(4)生成得到的新的栅格文件的空间分辨率是原有DEM的一半，使得矢量与栅格叠加运算时的空间精度得到进一步提升。以(10*10)平方米分辨率为例，按照文献[7]进行栅格判断时，每个面积栅格的数值至少为100平方米；按照本方法进行判断时，原有栅格被一分为四，每个栅格的数值至少为25平方米。栅格划分越细则越能精确的描述几何对象的边界。

表1 表面积统计结果

3.2 CVOA在栅格与矢量叠加统计时的优势

CVOA顾及了栅格与矢量多边形叠加统计时多边形边界对栅格的精确裁剪，它解决了传统GIS软件中对于栅格与多边形部分相交时栅格要么完全属于要么完全不属于多边形的“二值化”弊端，如果栅格与多边形数量越多则这种“二值化”处理的误差累积也有可能越来越大，使得最终计算的表面面积结果与实际数据之间存在相当大的差异。从结果中也看出在仙桃市沙地地类统计时甚至出现了表面积比平面投影面积少的情况，而在DEM为正的情况下这种情况理论上是不可能存在的。此外CVOA尽量减少了空间相交的次数，它用栅格的一整行的外接矩形框(也是矢量)，而非逐个栅格边框与多边形相交，再按照相交多边形各个节点的坐标推算点在栅格中的位置信息。与逐像元相交动辄几个小时的处理时间相比，CVOA完成统计的时间均在10分钟以内。由此可见CVOA适合于大规模的工程应用中。

3.3 表面积与投影面积

本文选取的三个地区仙桃市、罗田县以及神农架林区代表了三类典型的地形地貌区：平原、丘陵和山地。我们定义一个平整系数来评估表面积与平面投影面积之间的相对差异,如公式(8):

(8)

式中：fc为平整系数，SA为表面面积，PA为投影平面面积。

计算表明仙桃市、罗田县以及神农架林区的平整系数分别是1.004 5,1.033 4,1.115 0。由此可知地形起伏越大的地方地表真实面积与投影面积的相对差异越大。从第三部分的三个县的统计表格中D2结果来看，绝对数量上，三个县的面积差异也分别达到了11.43 km2, 71.27 km2, 371.58 km2。这样的差异对于评估研究区的固碳能力、生物资源、土地资源规模带来了较大的误差。换言之,在遥感数据的面积概念选择中,不应一味地使用垂直投影面积,而应根据自己所需,在条件允许的情况下适当选择地表真实面积的概念,否则将会引起较大的误差,甚至得出错误的结论[24]。

4 结论

本文中，作者提出了一种顾及边界精确裁剪的栅格与矢量叠加统计算法(CVOA)并将它应用在了湖北省不同地貌类型区县的地类表面积统计中。作者从两方面来描述CVOA:基于DEM构建表面积栅格以及用生成的表面积栅格与用地类型矢量进行叠加统计。该文主要得到以下三个结论：

(1)在不同的地貌区，投影面积并不能替代真实的表面积，两者之间存在着较大的差异，且随着地形起伏加大，这种差异也变得越来越大。

(2)栅格与矢量叠加统计时，CVOA保证了矢量多边形边界对栅格像元的精确“裁剪”，统计结果更真实可靠。同时CVOA极大地减少了空间相交的次数，计算高效，适合于大规模的工程应用中。

(3)真实地表面积具有广泛的应用前景。在区域资源评价(如林业资源评估，粮食产量预测)以及生态地理学研究(如固碳能力评价、生态服务价值计算)中，这些都需要表面积这一基础数据的支持。

作者贡献说明：本文为第一作者与通讯作者共同完成。第一作者于2015年12月～2016年08月在通讯作者何青松的指导下进行了相关领域的学习并起草了该文的写作。通讯作者在原文的基础上进行了整体的修改。实验部分(数据预处理、算法的编程以及栅格与矢量统计)由通讯作者完成。

[1] Hoechstetter S, Thinh N X, Walz U. 3D-Indices for the Analysis of Spatial Patterns of Landscape Structure[M]. Intercarto-Intergis. 2006.

[2] Gao X, Chun L U, Yun L,etal. Ecological assets valuation of the Tibetan Plateau[J]. Journal of Natural Resources, 2003，18(2):189-196.

[3] Li J, Wang W, Hu G,etal. Changes in ecosystem service values in Zoige Plateau, China[J]. Agriculture Ecosystems & Environment, 2010, 139(4):766-770.

[4] Liu Y, Li J, Zhang H. An ecosystem service valuation of land use change in Taiyuan City, China[J]. Ecological Modelling, 2012, 225(3):127-132.

[5] Zhou T, Chen B M, Liu G,etal. Biodiversity of Jinggangshan Mountain: the importance of topography and geographical location in supporting higher biodiversity[J]. Plos One, 2015, 10(3)：e0120208.

[6] Eisenlohr P V, Alves L F, Bernacci L C,etal. Disturbances, elevation, topography and spatial proximity drive vegetation patterns along an altitudinal gradient of a top biodiversity hotspot[J]. Biodiversity & Conservation, 2013, 22(12):2767-2783.

[7] Jenness J S. Calculating landscape surface area from digital elevation models[J]. Wildlife Society Bulletin, 2004, 32(3), 829-839.

[8] Wakelyn L A. Changing habitat conditions on bighorn sheep ranges in Colorado[J]. Journal of Wildlife Management, 1987, 51(51):904-912.

[9] Rosenzweig M L. Species diversity in space and time. Species diversity in space and time[M]. Cambridge University Press, 1995.

[10] 程乾, 王人潮. 数字高程模型和多时相MODIS数据复合的水稻种植面积遥感估算方法研究[J]. 农业工程学报, 2005, 21(5):89-92.

[11] Gregory A. Pope. Interal weathering in quartz grains[J]. Physical Geography, 2013, 16(4):315-338.

[12] Beasom S L, Wiggers E P, Giardino J R. A technique for assessing land surface ruggedness[J]. Journal of Wildlife Management, 1983, 47(4):1163-1166.

[13] Hodgson M E. What cell size does the computed slope/aspect angle represent?[J]. Photogrammetric engineering and remote sensing, 1995, 61:513-517.

[14] Kundu S N, Pradhan B. Surface area processing in GIS. GIS Development. 2004. (https://www.researchgate.net/publication/233390687_Surface_area_processing_in_GIS).

[15] Zhang Y, Zhang L N, Yang C D,etal. Surface area processing in GIS for different mountain regions[J]. Forestry Studies in China, 2011, 13(4):311-314.

[16] Berry J K. Use surface area for realistic calculations[J]. Geoworld, 2002, 9(2):11-14.

[17] Song G, Chen Y, Zhou Y. Algorithm for Estimating Mountainous Surface Area Based on GPS Data. Proceedings of the 2nd International Conference on Green Communications and Networks 2012 (GCN 2012): Volume 2[R]. Springer Berlin Heidelberg, 2013:679-687.

[18] 张伟, 李爱农. 基于SRTM DEM数据的全国地表面积计算研究[J]. 地理与地理信息科学, 2014, 30(3):51-55.

[19] Wang K, Lo C P. An assessment of the accuracy of triangulated irregular networks (tins) and lattices in arc/info[J]. Transactions in GIS,1999, 3(2), 161-174.

[20] 谢成磊, 赵荣, 梁勇. 基于地理坐标的地理国情统计单元表面面积精确计算[J]. 遥感信息, 2014(4):47-51.

[21] 江帆, 吕晓华, 王仲兰. 基于复化公式的DEM表面积算法分析[J]. 测绘学院学报, 2005, 22(4):263-265.

[22] 伍光和. 自然地理学[M].北京：高等教育出版社，2000.

[23] O'Rourke, J. Computational Geometry in C. Computational geometry in C[M]. Cambridge University Press, 1998.

[24] 李文航, 龚建华. 遥感地表真实面积和垂直投影面积差异的定量化模拟[J]. 计算机应用研究, 2008, 25(4):983-985.

责任编辑 喻晓敏

P3;TP3

A

1003-8078(2016)06-0048-07

2016-09-19 doi 10.3969/j.issn.1003-8078.2016.06.14

高昂，男，湖北黄冈人，黄冈中学学生。

何青松，男，安徽合肥人，博士，主要研究方向为制图与地理信息。