基于Bernstein多项式的双正交小波滤波器设计

古丽米热·米吉提，吐尔洪江·阿布都克力木，黄允浒，地里木拉提·玉买江

（新疆师范大学 数学科学学院，新疆 乌鲁木齐 830017）

基于Bernstein多项式的双正交小波滤波器设计

古丽米热·米吉提，吐尔洪江·阿布都克力木*，黄允浒，地里木拉提·玉买江

（新疆师范大学 数学科学学院，新疆 乌鲁木齐 830017）

自适应Bernstein多项式用于一类双通道双正交小波滤波器组的设计。该滤波器组属于半带对滤波器类，并用两个核函数定义。自适应Bernstein多项式是用来构建核函数。Bernstein多项式的参数设计是通过最小二乘法实现。第一步，分解低通滤波器的设计。第二步，设计重构低通滤波器。用两阶段方法，设计过程是有效的，包括求解线性方程组。该设计方法可以方便地设计不同的特性。

半带对滤波器组；自适应Bernstein多项式；最小二乘法；双正交小波滤波器组

离散小波变换用于许多需要信号分解的应用。小波滤波器的设计是相当于完全重构（PR）滤波器组的设计。传统滤波器组设计与小波滤波器设计的主要区别是在后者的情况下，对正则性的施加。正则性是通过施加零点的混叠频率，（对于双通道的情况下，在z=-1处是零）。完全重构条件和正则性条件给滤波器系数施加约束，这会使设计过程复杂化。设计过程基本上是数量的优化系数和正则性的限制[1]。

在文献中筛选的滤波器组有大量的设计方案。因为它们需要使用相当复杂的优化算法，所以它们中的许多是相当复杂的（通常是迭代的）。在信号处理的许多领域中使用最小二乘法和它的变体（并在数值的分析中），而且它的普及来源是很容易应用的，通常给出了很好的结果。Phoong等[2]提出的对半带对滤波器类的设计一个简单的方法。半带对滤波器具有许多吸引人的特点，包括完全重构滤波器的结构，实现效率和简单的设计。半带对低通滤波器是一种半带低通滤波器，在小波分析的术语半带低通滤波器是对应一个插值尺度函数[3]。半带对低通滤波器是由两个核函数定义的，但在大多数情况下，两个核函数是相同的，于是设计是一阶段过程。

文章采用了一个两者的核函数不同的两阶段的设计过程。在设计过程的每个阶段，采用最小二乘法，并涉及一个非线性方程组的非迭代过程。Bernstein多项式是用核函数的构造。Bernstein多项式通常用在函数逼近，光滑单调逼近问题。Bernstein多项式采用不仅单调逼近性能，而且具有结构特性，这是有用的小波滤波器组设计。

1 半带对滤波器组和Bernstein多项式

文章提到的滤波器属于双正交的半带对滤波器类[2]。低通滤波器由下面（1）式和（2）式确定：

其中z0(z)和z1(z)是从半带对滤波器得到的核函数。也就是1/2(1+z0(z))和1/2(1+z1(z))是半带滤波器。由此得到了高通滤波器：

和滤波器实现完全重构滤波器组，核函数的设计是通过使用Bernstein多项式的参变量。

首先介绍自适应Bernstein多项式[4]：

其中N为奇数，α=[α0,α1,...,α(N-1)/2]T和

半带对滤波器的Z变换传递函数是由x=（1/4）z(1-z-1)2替换代入（4）式得到的，核函数由下式给出：

文章认为在一般情况下核函数z0(z)和z1(z)是彼此不相同的。在文献［2］中所有设计实例z0(z)=z1(z)。在文献［4］中频谱因式分解需要进行滤波时，参数的Bernstein多项式来设计正交小波滤波器。从而为了自由参数αi的设计，［4］中得到了不对称的滤波器。为了自由参数的最小二乘设计，文献［5］中提出了单程的方法，但这不是一个合适的方法。为滤波器H0(z)所需的正则性（在z=-1处的零点重数）2（LH+1），可以通过αi=0(i=0,...LH)的设置来实现。对于F0(z)正则性是2(min(LH,LF)+1),βi=0(i=0,...LF)。使用半带对滤波器和自适应Bernstein多项式的优点是完全重构滤波器组和正则性约束的结构性施加。需要进行优化的剩余非零参数是无约束的，是四阶正则性的。

2 自由参数的最小二乘设计

值得注意的是，（9）式中的滤波函数是自由参数αi的线性函数和（10）式中的滤波函数是自由参数βi（当αi固定时）的线性函数。

在设计过程中，有两组自由参数α和β被待定了。滤波器H0只依赖于α，但是滤波器F0依赖于α和β。同时设计两套参数，将采用两阶段的方法。

第一步：参数α首先被优化的H0确定。

第二步：参数β被优化F0与从第一阶段确定的固定值α确定。

为了方便，（9）式和（10）式的一般形式由如下表示：

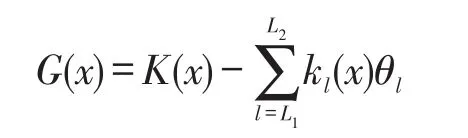
其中G(x)可以是H0或F0之中任意的，θl可以是αl或βl之中任意的。现考虑以下目标函数：

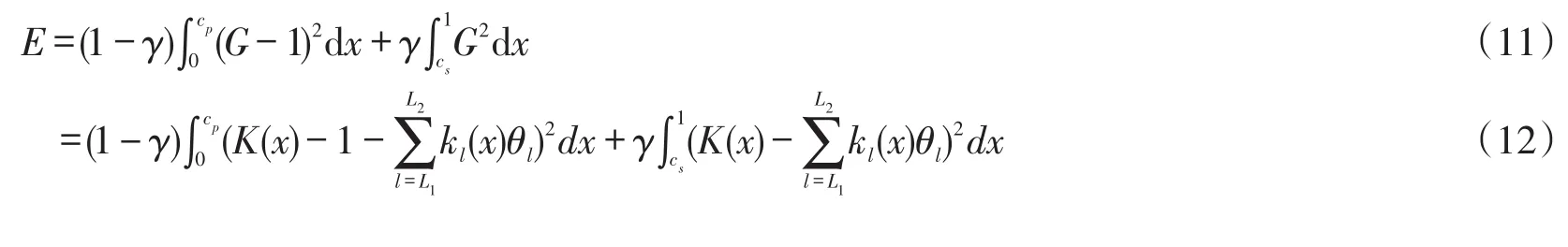
其中0≤λ≤1。cs和cp分别表示阻带边缘和通带边缘。现E是θl的二次函数。E还代表通带波纹能量和阻带波纹能量的加权总和。因为H0半带滤波器，所以考虑阻带的对称性是必要的。通过求解联立方程组的最优值，得到了最优值θl（通过最小化E）（类似于Wiener-Hopf或自适应滤波理论建立的正规方程组）：

其中 θ=[θL1,θL1+1，...,θL2]，并R=[rlm]和P=[pl](0≤l,m≤L2-L1)的元素分别：

通过R矩阵的逆矩阵来解决是最直接的方法。然而，R是一个实的、对称的、正的矩阵。所以计算效率的Cholesky分解法[6]可以用。对于小阶矩阵，前者的方法将满足。

下面与特征滤波器比较，通过扩大（12）式，得到

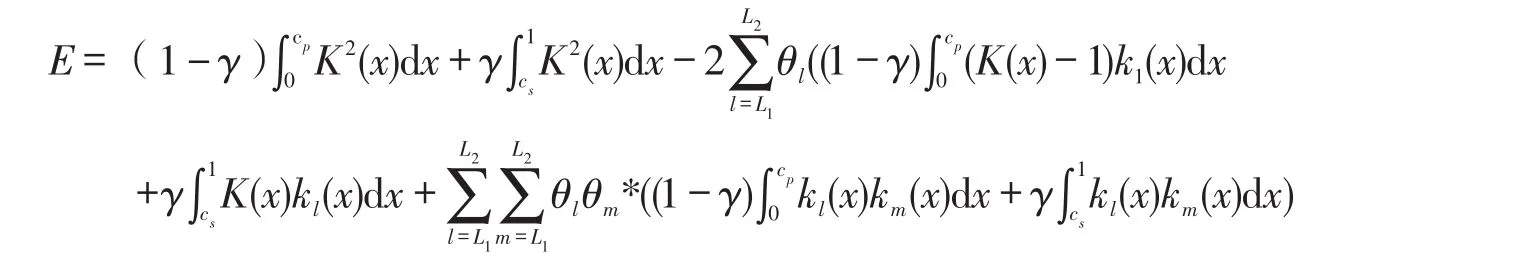
上述表达式可以用下面的向量矩阵形式表示，即

通过定义增广向量θ͂为θ~=[ ] θ0，θT，其中θ0≡1和增广矩阵R͂为

方程（14）可表示为

3 设计实例

N=7和M=7，滤波器H0和F0长度分别是15和29。假设LH=LF=1(α0=α1=β0=β1=0)。这两个滤波器是四阶正则性，即z=-1处，每个滤波器有4个零点。高通滤波器H1的频率响应（见（3）式）将显示H0的代替。

用δs表示阻带波纹的最大值和用δp表示通带波纹超调（从1的理想值）。

例1：对H0有cs=0.655，对F0有cs=0.727和γ=1即只有阻带波纹被认为是在优化。优化的自由参数值为

如图1所示的也是H1滤波器应用单阶段的方法，即αi=βi。

H1的阻带波纹在两阶段案例中比单阶段案例小：δs=-34dB（两阶段）对比于δs=-23dB（单阶段）。H1的通带超调也在两阶段案例中小：δp=0.102（两阶段）比较与δp=0.125（单阶段）。然而，在第一阶段里，转型期（过渡期）的衰减是更清晰的。在两阶段方法中，F0滤波器响应的形成有更多的灵活性。

图1 滤波器组的频率响应

例2：对H0和例1中一样，对F0来说，cp=0.5,cs=0.727和γ=0.25。即通带波纹和阻带波纹在优化中被考虑。优化的自由参数值为(β0,β1,β2,β3)=(0,0,0.366,0.832)。

图2显示滤波器对的频率响应。例1中的结果也在图2显示。与例1比较，通带超调δS较小（0.075与0.102相比），但是阻带波纹δS较大（-28dB与-34dB相比）。图6显示有例2中的低通滤波器产生尺度函数，由于z=-1时，存在足够的零点，所以是合理的。最终，虽然没有明确说明的例子，在过渡衰降与波纹幅度中，通过调整cp和cs的值，也有一个机理去调控清晰度。

图2 滤波器对的频率响应

4 结论

基于自适应Bernstein多项式的双正交小波滤波器的设计，半带对滤波器类和Bernstein多项式被使用了，这确保了结构性施加的完全重构和正则性约束。设计的每一阶段，应用了最小二乘准则，这导致了涉及解决一组线性方程组的一个简单的设计过程。正规方程的技巧也与特征滤波器方法相比较，用于求解最小二乘问题。这解释了为什么后者不是一个合适的方法。设计实例来说明设计技术的有效性。

［1］吐尔洪江·阿布都克力木.小波信号处理基础［M］.北京：北京邮电大学出版社，2014.

［2］于梦，云利军，等.基于多尺度Retimex算法结全PCA特征加权的人脸识别方法［J］.云南师范大学学报（自然科学版），2016，36（6）：25-31.

［3］S.M.Phoong，C.W.KIM，etc.A new classof two-channelbiorthogonal filterbanksandwaveletbases［J］.IEEETrans.SignalProcess，1995，43（3）：649.

［4］W.Sweldens.The lifting scheme：A custom-design ofbiorthogonalwavelets［J］.Appl.Harmon.Anal.，1996，3（2）：186-200.

［5］H.Caglar，and A.N.Akansu.A generalized parametric PR-QMF design technique based on Bernstein polynomial approximation［J］.IEEE Trans. SignalProcess.，1993，41（7）：2314

［6］T.Cooklev，A.Nishihara，and M.sablatash.Regular orthonormaland biorthogonalwavelet filter［J］.Signal Process，1997，57：121-137.

［7］G.H.Golub and C.F.Van loan.Matrix computations［M］.The John HopkinsUniversity Press，1985.

［8］R，A.Horn and C.R.Johnson.Martix analysis［M］.Cambridge University Press，1985.

Design of Doub le OrthogonalW avelet Filter based on Bernstein Polynom ial

GULIMIRE·Mijiti,TUERHONGJIANG·Abudoukelimu，HUANG Yun-hu，DILIMULATI·Yumaijiang

（School ofMathematical Sciences,Xinjiang Normal University,Urumqi，Xinjiang,830017,China）

Bernstein polynomial is employed for the design ofa class of two-channelbiorthogonal filter banks. The filter banks belong to the class HPFB(halfband pair filter bank)and are defined by two kernels.The parametric Bernstein polynomial is used to construct the kernels.the design of the free parametersof the Bernstein polynomial is achieved through a least squaresmethod.In the first stage,the analysis low-pass filter is designed and in the second stage,the synthesis low-pass filter is designed.With the two-stage approach,the design process is efficient and involvessolving linearequations.The design techniqueallows filterswith differentcharacteristics tobe designed easily.

Halfband pair filter bank;Bernstein polynomial;Least squaremethod;Biorthogonalwavelet filter bank

TN713.1

A

1008-9659（2016）04-0035-04

2016-09-28

国家自然科学基金资助项目（11261061，61362039，10661010）；新疆维吾尔自治区自然科学基金资助项目（200721104）。

古丽米热·米吉提（1991-），女，新疆乌鲁木齐人，硕士研究生，主要从事小波分析及其应用方向的研究。

*［通讯作者］吐尔洪江·阿布都克力木（1962-），男，新疆博乐人，教授，博士，主要从事小波分析及其应用方向的研究。