基于遗传粒子群算法的番茄幼苗光合优化调控模型

王 东，王智永，裴 雪，辛萍萍，张佐经

（西北农林科技大学机械与电子工程学院，杨凌 712100）

基于遗传粒子群算法的番茄幼苗光合优化调控模型

王 东，王智永，裴 雪，辛萍萍，张佐经*

（西北农林科技大学机械与电子工程学院，杨凌 712100）

番茄光合速率主要受温度和光子通量密度影响，动态获取不同温度条件下的光饱和点信息是提高光环境调控效率的关键。该文结合遗传粒子算法提出了一种光合优化调控模型：利用光合速率双因素嵌套试验获取多维数据，构建温度、光子通量密度耦合的光合速率多元非线性回归模型，采用遗传算法对光合速率模型进行优化，获取任意离散温度值下的光饱和点，以饱和光照强度作为目标值建立光合优化调控模型。以番茄幼苗为例进行了验证，试验结果表明：提出的方法可动态获取不同温度条件下光饱和点，光饱和点实测值与计算值决定系数为0.9873，最大相对误差小于4.6%，具有较高精度，对提高设施光环境调控效率具有重要的意义。

番茄；幼苗；光合速率；光饱和点；遗传算法；粒子群算法；调控模型

番茄是我国的主要设施作物之一，每年总产量世界领先［1］。番茄作为光敏感作物，光照不足会造成其产量大幅下降［2］。光合作用是描述作物有机物质积累的过程，不仅受光照影响，且受温度、二氧化碳浓度等环境因子影响［3-5］，为实现设施番茄光环境高效调控，提高其产量与品质，番茄光合速率研究广泛开展。其中蒋燕等［6］、张富存等［7］研究表明温度过低或过高均会导致番茄幼苗光合速率降低，说明温度和光照是影响光合速率因素中的两个主要因素［8］；胡瑾等［9］采用遗传算法进行光温匹配寻优，为本试验设计有一定借鉴作用。因此，探究温度、光照环境信息与光合速率间对应关系，寻找不同环境下使番茄达到最大光合速率的饱和光强，建立番茄光合优化调控模型，是提高番茄产量的重要途径。

为实现基于作物需求的光合最优调控，光合速率模型作为其理论基础得到广泛研究。其中李天来等［10］研究建立了基于温度修正的番茄光合速率模型；赖琳玲等［11］研究发现随温度、光照变化番茄生长的变化规律；以色列、美国等科学家合作开发了TOMGRO温室番茄模型；荷兰科研人员开发的HORTSIM作物模拟器是目前该领域的典型代表［12-13］，以上研究均建立了温度与光子通量密度关联的光合速率模型，为本试验研究提供了依据，但真正的按需调控应建立在不同环境下光饱和点拟合的基础上，而上述模型未实现光饱和点寻优，因此构建番茄光合速率模型，设计寻优算法获取光饱和点，是建立光合调控模型的关键。

遗传算法与粒子算法是实现高效精准寻优的常用手段。目前，在遗传粒子群算法上，国内外学者也做了不少的研究。其中蔡雁等［14］采用遗传粒子寻优算法获取最优铁矿粉库存量，为钢铁企业的科学采购提供依据；张干清等［15］基于杂交GA-PSO算法的结构协同优化，结果表明提出的杂交GA-PSO协同算法较GA与PSO算法有更快的收敛速度，当相关系数为0.7时，可使该行星架的总体积减小7.06%；陈双等［16］提出了车辆主动悬架的遗传粒子群LQG控制方法，其结果表明车辆主动悬架的遗传粒子群LQG控制方法；Abd-El-Wahed等［17］采用集成粒子群算法与遗传算法对非线性问题进行了优化；Ricardo等［18］提出了一个混合型GA-PSO优化方法的模糊逻辑控制器（FLC）的自动设计，以尽量减少植物反应的稳态误差，仿真结果表明了该优化方法对控制应用的可行性；Lee等［19］在数值约束和网络分解的基础上使用混合GA-PSO对基因调控网络进行推断，结果表明了该方法的有效性。以上研究可为最优需光调控模型建立提供依据，但光饱和点寻优易受算法参数、适应度函数、寻优范围等条件影响，造成较大误差。

为此，本研究结合遗传算法和粒子群算法的的优点，以温光耦合的番茄光合速率模型为基础，采用遗传粒子群算法对光饱和点进行寻优，得到各温度值下的最优解，进一步建立以饱和光强为目标的番茄光合优化调控模型，为番茄光环境调控提供有效手段。

1 材料与方法

1．1 试验材料

试验于2015年3—6月在西北农林科技大学南校区玻璃温室内进行。对象为处于幼苗期的番茄，品种为‘毛刺802’，种植数量为200株。

1．2 试验方法

选取定植后植株生长状况差异较小、健壮的番茄幼苗进行试验，测量设备为Li-6400XT型便携式光合仪，该光合仪可按需控制测量叶室的小环境，以设置不同试验条件。试验时选择9：00—11：30和14：30—17：30两个时间段，以避免“午休现象”；设定二氧化碳浓度为300 μmol·mol－1；6个温度梯度为16℃、21℃、25℃、29℃、33℃、37℃；10个光子通量密度梯度为0 μmol·m－2·s－1、50 μmol·m－2·s－1、100 μmol·m－2·s－1、200 μmol·m－2·s－1、400 μmol·m－2·s－1、600 μmol·m－2·s－1、800 μmol·m－2·s－1、1 000 μmol·m－2·s－1、1 200 μmol·m－2·s－1、1 500 μmol·m－2·s－1。在60组试验条件中，每组试验均选取6株幼苗重复测量6次净光合速率值，共形成360组样本数据。

1．3 试验数据处理

按狄克松准则［20-21］对测量数据进行预处理，完成粗大误差剔除，该准则判断粗大误差从最大抽样值和最小抽样值入手。在测量中，对同一指标进行多次等精度重复测量，降低测量误差。

根据狄克松准则对本试验进行粗大误差滤除后，测得剩余样本的平均值如表1所示。通过计算，可得到该30组数据的方差小于0.27，由此表明采用狄克松准则进行粗大误差分析及滤除的效果较好。

2 光合作用优化调控模型建立

分三步建立调控优化模型：首先根据处理后的数据利用非线性拟合方法建立3元番茄净光合速率模型以得到寻优目标函数，然后采用遗传-粒子群组合智能算法对光合速率进行寻优，最终依据寻优得到的光饱和点建立光合优化调控模型。

表1 试验所得光合速率值Table 1 Photosynthetic rate values obtained from testsμmol CO2·m－2·s－1

2．1 多因子耦合光合速率模型

经过分析，综合考虑拟合精度及计算复杂性，确定采用3元5次非线性方程进行回归分析，建立以温度、光子通量密度为自变量的光合速率模型，如式（1）所示，拟合结果如图1。

式中，T：温度/℃；PFD：光子通量密度/μmol·m－2·s－1；Pn：光合速率/μmol CO2·m－2·s－1。

图1 光合速率拟合图Fig．1 Fitting of photosynthetic rates

在相同温度条件下，光合速率随着光子通量密度增大而增加，在最大值附近趋于变化平缓，但光子通量密度进一步增大时，光合速率会减小；当光子通量密度恒定不变时，随着温度的升高光合速率也呈现相似的先升后降的趋势。以上结果与前人研究结果相符［22-23］，且具有良好的拟合效果，说明试验方案合理。为充分考虑各因子之间的交互作用，构建非线性回归净光合速率模型，模型拟合结果的决定系数为0.9929，相比于现有模型，所构建的光合速率模型具有更好的拟合结果。

2．2 基于遗传粒子群算法的光温耦合寻优算法

遗传算法是借鉴生物界适者生存法则的进化算法，被用于解决寻优问题。遗传算法不容易陷入局部最优，同时适应大规模的并行计算。算法通过复制、交叉、突变等操作产生下一代的解，适应度低的解将被淘汰掉，将适应度高的解保存下来。遗传算法的优越性主要表现在：具有群体搜索和内在启发式随机搜索的特性，不易陷入局部最优；遗传算法固有的并行性和并行计算的能力，非常适用于大规模并行计算。本研究在粒子群算法中引入遗传算法的变异算子来增强粒子群算法跳出局部最小值的能力。同时通过引入种群分割策略来维护种群的多样性，使得各子种群分别进化，子种群之间的相互竞争避免了算法进化过程中陷入局部最优解。

本研究以番茄幼苗不同温光环境的光合速率值构建样本数据，建立光合速率模型，设计遗传粒子寻优算法对光合速率模型进行寻优，获取最优光合速率解及其对应的饱和光强，具体流程如图2。

GA-PSO具体算法步骤如下：

1）基于多因子耦合光合速率模型，确定该种群规模为20，由于在该试验中，个体为温度与光子通量密度，所以设置个体长度为2，根据经验，进化代数设为100较为合适。

2）由于本试验采用了遗传算法的交叉和变异算子，需要设定其概率参数。不同的交叉概率和变异概率寻优结果会产生较大差异，交叉概率越大，可越快到达最优目标值区域，变异概率过大影响寻优过程的稳定性，因此本文选取交叉概率为0.7，变异概率为0.01。又因为本试验还采用了粒子群算法，所以还需要设置粒子的位置和速度。温度粒子是特定的，无需设置；由实际测试得到的光子通量密度可知，其最小值不可能为负，所以设定其下界为0，其最大值不超过1 300，所以设定1 300为其上界，最终设置光子通量密度的初始位置范围为0—1 300；又根据对粒子群算法的学习，粒子飞行的极限方向是正反两个方向，因此设光子通量密度的速度范围为－800—1 000。

3）在特定温度条件下进行寻优，以2℃为步长构建寻优的温度样本集T＝（T1，T2，…，Tn），其中Tn＝Tmin+2n，Tmin代表特定最小温度值，n＝1，2，3，…。并以此样本集中数据完成对式（1）所示Pn＝f（T，PFD）的温度实例化。在此基础上，并基于上文的光合速率模型Pn＝f（T，PFD）确定适应度函数式（2）：

式中：F表示特定温度值Tn下的适应度函数。

4）利用rand函数随机产生初始光子通量密度粒子及其速度。由于rand函数产生随机数的范围在0—1之间，基于实际测试结果，我们用位置系数1 500和速度系数1 000调整光子通量密度粒子的位置范围和速度范围分别为0—1 500和－1 000—1 000。

5）利用式（2）计算初始化种群的适应度值，即特定温度下的光合速率值。找出特定温度下局部范围内的最大光合速率值，即个体最优位置pbest；再找出特定温度下全部范围内的最大光合速率值，即全局最优位置gbest。

6）接下来分别采用式（3）和（4）对光子通量密度粒子的位置和速度进行更新，以产生新的粒子；

式中：v（t）表示进化次数为t时光子通量密度的速度，PFD（t）表示进化次数为t时光子通量密度的位置，Fpbest（t）表示进化次数为t时局部最大光合速率值，Fgbest（t）表示进化次数为t时全局最大光合速率值，c1和c2为学习因子，根据经验，均设置为1.49445。

7）采用遗传算子对粒子执行交叉和变异操作。交叉操作如下：

图2 GA-PSO流程图Fig．2 Flowchart of GA-PSO

式中，akj为第k个染色体的第j个基因，aij为第i个染色体的第j个基因，b是0—1区间的随机数。采用如下变异操作过程：

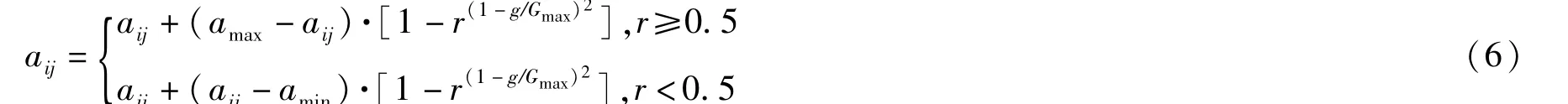
式中，amax是基因aij的上界；amin是基因aij的下界；r为0—1区间的随机数，g是当前迭代次数，Gmax是最大进化次数。

8）计算经过上述操作的个体的适应度值，并和个体最优pbest比较；若当前个体的适应度值比pbest大，则把该值作为新的个体最优位置，并接着与全局最优gbest比较；若仍比gbest大，则把该值作为新的全局最优位置，并判断是否满足最大进化次数100次的这个终止条件，若满足，则输出结果。若并未满足上述条件，则对粒子不断地进行位置和速度更新以及交叉变异操作，直至满足条件为止。

9）选取新一组温度重复步骤3—8，直至完成所有温度梯度下的寻优，结果如图3。GA-PSO寻优算法的具体参数如表2所示。

表2 遗传粒子群算法参数设置Table 2 Parameter setting of GA-PSO

图3 寻优进化图Fig．3 Evolutionary optimization figure

按上述步骤1—9分别对18℃，20℃，22℃，24℃，26℃，28℃，30℃，32℃，34℃等9个温度梯度进行光饱和点寻优，绘制光合速率随进化代数的变化曲线，如图3所示。

整体分析图3可以发现，该9组最佳温度与光照强度组合下所得到的最佳光合速率值的进化过程很稳定，无振荡，番茄最佳光合速率值基本保持不变，由此表明算法参数设置较合理。从进化过程来看，当进化代数较小时，最佳光合速率值缓慢增长，当进化至第十代时，最佳光合速率值基本保持恒定。在算法运行的过程中，不断实现个体进化，获取适应度高的种群个体，当接近最优解时产生的新的最优个体适应度值上升幅度不明显，最终趋于稳定。

3 光合优化调控模型构建

根据GA-PSO混合寻优结果绘制离散温度下光饱和点变化曲线，如图4所示。光饱和点随温度增加呈现先上升后下降趋势，与作物光合作用变化规律相吻合。

选取温度T为输入量，饱和光照强度PFD为输出量，通过非线性回归方法进行拟合，建立番茄幼苗光合最优调控模型，如式（7）所示，基于该模型，可获取任意温度条件下光饱和点数据。

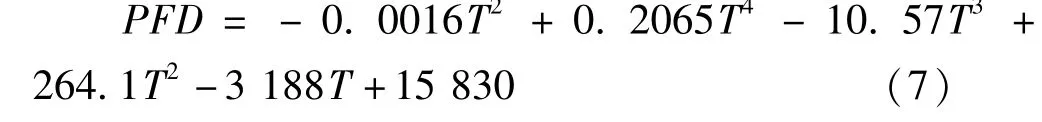
图4 离散温度下光饱和点变化曲线Fig．4 Variation of light saturation points at discrete temperatures

4 模型验证分析与对比

为评价调控模型的准确性与可靠性，对光饱和点计算值与实测值进行对比验证。使用Li-6400XT型便携式光合仪，测得16—36℃范围内13个温度下的光饱和点，以基于GA-PSO寻优结果建立的需光模型计算得到的13个温度值下光饱和点作为模拟值，实测值与模拟值二者之间的相关关系如图5-C所示。为了进一步说明模型的优劣，采用同样的方法基于GA、PSO寻优结果建立需光模型并验证实测值与模型模拟值二者之间的相关关系，如图5-A、5-B所示。

图5 光饱和点实测值与模拟值的相关性Fig．5 Correlation between the measured and simulated values of light saturation points

通过对图5所示光饱和点实测值与模拟值的相关性拟合可以得出，基于GA、PSO、GA-PSO三种寻优结果建立的需光模型，得到的决定系数分别为0.9732、0.9783、0.9837，接近于1，均方根误差分别为12.95、11.16、10.09，可以得出3种基于寻优算法的需光模型效果都较好，其中GA-PSO的效果最优。为了进一步说明模型的准确性，对13组试验结果进行光饱和点验证分析，其最大相对误差不超过4.6%（表3）。

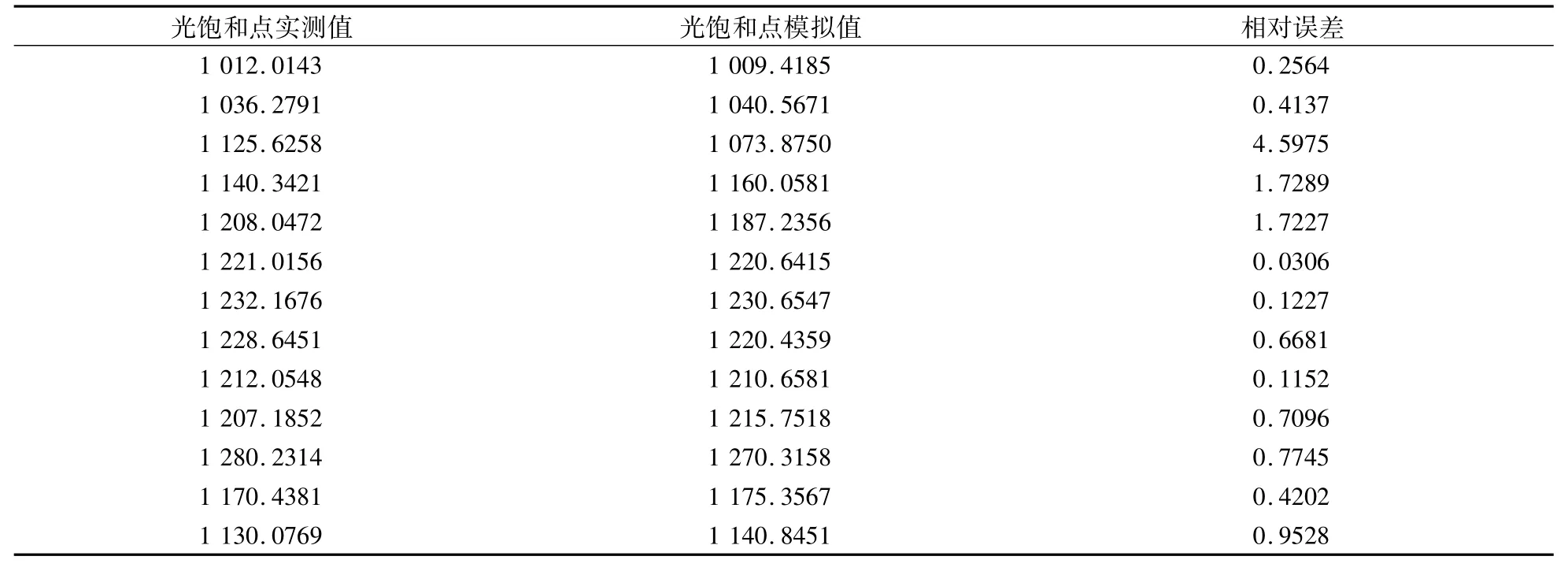
表3 光饱和点误差分析Table 3 Error analysis of light saturation points

根据表3验证分析可知，本文所建立的需光调控模型具有较高的精度。说明采用GA-PSO混合算法寻优比采用GA和PSO算法更准确。

5 结论

本文针对番茄光饱和点随温度动态变化的特点，将遗传算法（GA）和粒子群算法（PSO）相结合得到遗传粒子群算法，采用遗传粒子群算法（GA-PSO）对光温进行寻优，获取不同温度下光饱和点数据，以其为基础建立光合优化调控模型，利用番茄幼苗为例进行验证，具体结论如下：

（1）设计的嵌套试验，获取不同温度、光照对应的光合速率值，以其为样本数据构建番茄幼苗期光合速率模型。经验证，模型决定系数R2为0.9925，具有较强的泛化能力，可为光合速率预测提供有效手段。

（2）采用遗传算法和粒子算法对番茄幼苗光合速率模型进行寻优，得到离散温度值对应的光饱和点数据，以其为理论基础建立光合优化调控模型，利用试验数据对调控模型输出的光饱和点进行验证，结果表明，光饱和点计算值与实测值决定系数达0.9837，最大相对误差不超过4.6%，具有较高的拟合精度。

（3）本文提出的基于遗传粒子的光合优化调控模型，可实现以光饱和点为目标值的按需调控，从而克服不同作物的光合特性差异，为设施光环境高效调控提供理论基础。

［1］张春奇，查素娥，李红波.番茄育种研究概况及展望［J］.农业科技通讯，2011（3）：29-33.

［2］吴锴，张静，郝称意.温室番茄群体光合作用模拟模型的研究［J］.山西农业大学学报（自然科学版），2013，33（3）：225-229.

［3］王铭，李涛，李爱芬，等.光照、温度和pH对雨生红球藻光合特性的影响［J］.水生生物学报，2009，33（3）：400-405.

［4］郭尚，王宇楠.不同光照强度西瓜光合速率日变化的研究［J］.华北农学报，2011，26（5）：170-173.

［5］张治安，徐克章，陈展宇，等.影响人参叶片光合速率对CO2水平响应的因素［J］.南京农业大学学报，2006，29（2）：11-14.

［6］蒋燕，赵会杰.低温弱光处理对番茄幼苗生长的影响［J］.河南农业科学，2006（1）：87-91.

［7］张富存，张波，王琴，等.高温胁迫对设施番茄光合作用特性的影响［J］.中国农学通报，2011，27（28）：211-216.

［8］赵玉萍，邹志荣，杨振超，等.不同温度和光照对温室番茄光合作用及果实品质的影响［J］.西北农林科技大学学报（自然科学版），2010（5）：125-130.

［9］胡瑾，何东健，任静，等.基于遗传算法的番茄幼苗光合作用优化调控模型［J］.农业工程学报，2014，30（17）：220-227.

［10］李天来，颜阿丹，罗新兰，等.日光温室番茄单叶净光合速率模型的温度修正［J］.农业工程学报，2010，26（9）：274-279.

［11］赖琳玲，程智慧，陈学进，等.番茄器官生长动态与环境温度和光照关系的模拟［J］.西北农业学报，2010，19（2）：127-132.

［12］DAYAN E，VAN KEULEN H，JONES J W，et al.Development，calibration and validation of a greenhouse tomato growth model：I.Description of the model［J］.Agricultural Systems，1993，43（2）：145-163.

［13］GIJZEN H，HEUVELINK E，CHALLA H，et al.HORTISIM：A model for greenhouse crops and greenhouse climate［J］.Acta Horticulturae，1998，456：441-450.

［14］蔡雁，钟茜怡，吴敏，等.基于GA-PSO算法的烧结料场原料库存量优化［J］.化工学报，2012，63（9）：2824-2830.

［15］张干清，龚宪生.变量相关情况下基于杂交GA-PSO算法的结构协同优化［J］.机械工程学报，2012，48（15）：113-125.

［16］陈双，宗长富.车辆主动悬架的遗传粒子群LQG控制方法［J］.汽车工程，2015（2）：189-193.

［17］ABD-EI-WAHED W F，MOUSA A A，EL-SHORBAGY M A.Integrating particle swarm optimization with genetic algorithms for solving nonlinear optimization problems［J］.Journal of Computational and Applied Mathematics，2011，235（5）：1446-1453.

［18］RICARDO M S，OSCAR C，AGUILAR L T.Type-1 and Type-2 fuzzy logic controller design using a hybrid PSO-GA optimization method［J］. Information Sciences，2014，285：35-49.

［19］LEE W P，HSIAO Y T.Inferring gene regulatory networks using a hybrid GA-PSO approach with numerical constraints and network decomposition［J］.Information Sciences，2012，188：80-99.

［20］范满红，马胜前，陈彦，等.基于多传感器数据融合的温湿度监测系统［J］.压电与声光，2012，34（3）：459-462，465.

［21］刘志平.检测仪表中粗大误差的剔除分析［J］.电子测量技术，2009，32（11）：55-57，84.

［22］张洁，李天来，徐晶.昼间亚高温处理时期对日光温室番茄光合作用与产量的影响［J］.农业工程学报，2008，24（3）：193-197.

［23］张洁，李天来.日光温室亚高温对番茄光合作用及叶绿体超微结构的影响［J］.园艺学报，2005，32（4）：614-619.

（责任编辑：程智强）

A regulatory model of tomato seedlings’photosynthesis based on genetic algorithm-particle swarm optimization

WANG Dong，WANG Zhi-yong，PEI Xue，XIN Ping-ping，ZHANG Zuo-jing*
（College of Mechanical and Electronic Engineering，Northwest A＆F University，Yangling 712100，China）

Tomato plants’photosynthetic rate is mainly influenced by temperature and photon flux density，and acquisition of dynamic information of light saturation points at different temperatures is the crux of improving the regulating efficiency of light environment.According to genetic algorithm-particle swarm optimization（GAPSO）the paper proposes a regulatory model of photosynthetic optimization：multidimensional data are acquired by means of the two-factor nested tests of photosynthetic rate，a multivariate nonlinear regression model of photosynthetic rate coupling temperature and photon flux density is built and then optimized by using GA-PSO，thus acquiring the light saturation point at any discrete temperature，and lastly with the saturated light intensity as a desired value，a regulatory model of photosynthetic optimization is established.The model is verified by taking tomato seedlings，and the results show that the light saturation points at different temperatures can dynamically be acquired by the proposed method，the determination coefficient between the light saturation points’measured and calculated values is 0.9873，and the maximum relative error is less than 4.6%，indicating that the proposed method has a high precision and an important significance of improving the regulating efficiency of light environment.

Tomato；Seedling；Photosynthetic rate；Light saturation point；Genetic algorithm；Particle swarm optimization；Regulatory model

S641.2

A

1000-3924（2016）06-026-07

2016-10-11

国家自然科学基金资助项目（31501224）；陕西省农业科技创新与攻关项目（2016NY－125）

王东（1982—），男，硕士，讲师，研究方向：计算机在农业中的应用。Tel：13991838234，E-mail：wangdong510＠163.com

*通信作者：张佐经（1982—），男，讲师，主要从事无线传感器网络、智能检测与控制等方面研究。E-mail：zhangzuojing＠126.com