一道高考题的解法赏析与背景探究

☉江苏省如东县马塘中学 陈宝霞

一道高考题的解法赏析与背景探究

☉江苏省如东县马塘中学 陈宝霞

2016年全国Ⅰ卷试题，相较于前几年试题的难度而言，难度更大一些.有很多题目设计的都很有新意且意味深长，笔者以今年全国Ⅰ卷文科的第20题为例，试图给大家展示一下出题人的思路及该问题的设计背景.如有不足之处，欢迎大家指正.

一、试题呈现

题目在直角坐标系xOy中，直线l：y=t（t≠0）交y轴于点M，交抛物线C：y2=2px（p>0）于点P，M关于点P的对称点为N，连接ON并延长交抛物线C于点H.

（Ⅱ）除H以外，直线MH与抛物线C是否有其他公共点？说明理由.

二、解法赏析

解法1：（Ⅰ）由已知得M（0，t），P又N为M关于点P的对称点，故ON的方程为代入y2= 2px，整理得px2-2t2x=0，解得x1=0因此H所以N为OH的中点，即

（Ⅱ）直线MH与抛物线C除H以外没有其他公共点.理由如下：

所以除H以外，直线MH与抛物线C没有其他公共点.

点评：这个解法充分体现了坐标法思想，凸显了解析几何的解析味道，是学生必须掌握的方法，这个解法还从代数的角度证明了直线MH是抛物线过点H的切线.

解法2：（Ⅰ）同法一.

（Ⅱ）如图1，作HH1垂直于准线x=-，垂足为H1，交y轴于点Q，由（Ⅰ）知△H1QM≌△FOM，从而∠H1MQ=∠FMQ，H1，M，F三点共线，由|HF|=|HH1|，|FM|=|H1M|，得HM是线段H1F的垂直平分线.

图1

设直线MH上除H以外，与抛物线C还有一个公共点I，作准线的垂线II1，垂足为I1，连接IH1，IF.因为I是H1F垂直平分线上的点，所以|IH1|=|IF|.又I是抛物线y2=2px上的点，所以|II1|=|IF|，所以|IH1|=|II1|，与△II1H1为直角三角形矛盾，所以除H以外直线MH与抛物线C没有其他公共点，即直线MH为抛物线的切线.

点评：这个解法紧扣抛物线的定义及平面几何的相关知识，回归本质，凸显了解析几何的几何味道.从解答过程而言，该题并不复杂，最大的难点在于涉及的点太多，且所有的量均是未知的（除了原点）.该题与我们平时练习的“套路”相去太远，学生感觉到陌生，再加上在前面消耗的时间过多，已经没有精力能平静地面对该问题.

三、寻根探源

本题来源于《人教A版数学选修1-1》56页：“信息技术应用——用‘几何画板’画图，如图2，F是定点，l是不经过点F的定直线，H是l上任意一点，过点H作MH⊥l，线段FH的垂直平分线m交MH于点M，拖动点H，观察点M的轨迹.你能发现点M满足的几何条件吗？”

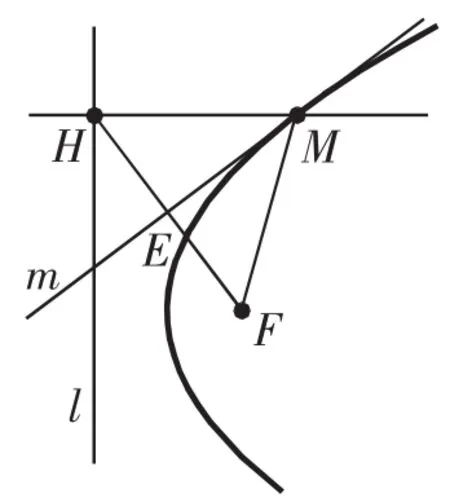
图2

教科书设置“信息技术应用”栏目，给出了抛物线生成的过程.通过“几何画板”的制作，学生可以从作法中了解曲线上的点所满足的几何条件，明确抛物线的定义，用几何画板作抛物线的方法，依据就是这个栏目.但该栏目的作用绝不是仅此而已，它还给我们留下了如下宽广的探究空间.

结论1：点M的轨迹是抛物线C，则与之相关的垂线m与抛物线C相切，点M为切点，如图3.

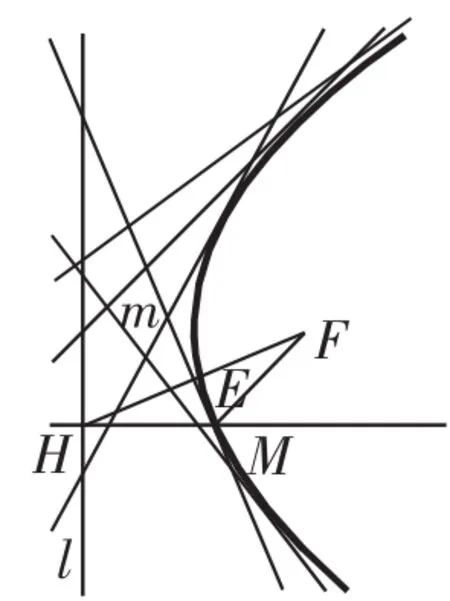
图3

可以从代数和几何两个角度来证明垂直平分线m是抛物线过点M的切线，其证法与这道高考题的证法完全相同，具体证法略.

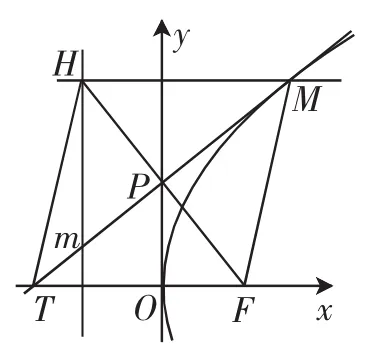
图4

结论2：如图4，若直线m与x轴相交于点T，则四边形MHTF为菱形.

简证：设M则H再由F得直线m的方程为即

四、拓展延伸

通过解答过程，该题的本质是讨论过抛物线外一点作抛物线的切线，以及对应的切点弦相关的性质，可以得到相应的一系列性质：

引理已知抛物线y2=2px（p>0），则过抛物线上一点M（x0，y0）的切线方程为y0y=p（x+x0） ①.

证明：根据隐函数的求导法则，对抛物线方程求导可得则在点M（x0，y0）处切线的斜率为直线①过点M（x0，y0）且斜率为所以结论成立.该证明过程涉及高等数学知识，也可联立直线①与抛物线的方程，通过验证Δ=0说明结论.

定理1已知抛物线y2=2px（p>0），过抛物线外一点M（x0，y0）的切点弦方程为l：y0y=p（x+x0），并称该直线为关于点M的切点弦方程.

证明：易知过抛物线外一点M作抛物线的切线一定有两条，设对应的切点为A，B.设点A的坐标为（x1，y1），根据引理，知直线MA的方程为y1y=p（x+x1）.

同理设点B的坐标为（x2，y2），则直线MB的方程为y2y=p（x+x2）.

因为点M∈直线MA，所以y1y0=p（x0+x1） ②成立.

同理，y2y0=p（x0+x2） ③也成立.构造直线l：y0y=p（x+ x0），由②、③式可知，点A，B∈l，再根据两点确定一条直线，所以直线l即为对应的切点弦.

如果以此为背景，回到原题第（Ⅱ）问，我们并不需要知道点H的坐标，通过验证ON的斜率即可获得结果.

改写解答如下：可知M（0，t），根据定理1，点M对应的切点弦为lM：ty=px，该直线显然过原点O，由第（Ⅰ）问可知即直线ON为关于点M的切点弦，故点H为切点.

再联系第（Ⅰ）问，可知点N是线段OH的中点，直线MN与对称轴平行.是否所有的切点弦都有这样的特性呢？如果有，根据切点弦的唯一性，直接可得答案.

定理2过点M（x0，y0）作抛物线y2=2px（p>0）的切线，设两切点为A，B，则有AB的中点N的纵坐标为y0，即与点M的纵坐标一样，即直线MN与抛物线的对称轴平行.

证明：（点差法）设点A（x1，y1）满足抛物线方程，得=2px1.设点B（x2，y2）也满足抛物线方程，得=2px2.两式相减得（y1-y2）（y1+y2）=2p（x1-x2），化简为即有yN=

再次改写解答如下：已知点O为切点，由第（Ⅰ）问N是线段OH的中点，根据定理2及切点弦的唯一性，直线ON为关于点M的切点弦，故点H为切点.

根据题干可知点N与点M关于点P对称，这是否也是一般结论呢？

定理3过点M（x0，y0）作抛物线y2=2px（p>0）的切线，设两切点为A，B，设AB的中点为N，则MN的中点P落在抛物线上.

证明：由定理2，知yN=y0，再根据定理1，得直线AB的方程为：y0y=p（x+x0），可得点N的横坐标为即有点N的坐标为再根据点M（x0，y0）可得点P的坐标为所以点P在抛物线上.

五、教学启示

本题涉及切点弦相关的知识，如果学生熟悉该背景，入手会更容易，在解答的过程中会更有方向感；即使学生并不知道相关的背景知识，学生依然能解答此题.所以此题的设计是很巧妙的，可以说是深入浅出.在以后的教学中，首先要教会学生稳定心态，即使读不懂该题，利用“相关点”法也能获得一些分数：即设出点M的坐标，利用题目条件写出相关的点P与点N，再到下一层“相关点”，求出点H的坐标.告诫学生对于难题，我们没必要获得完整的解答，在自己的能力下，做到“最好”就足够了.其次，在平时的教学中，在讲解“套路”的基础上，给学生介绍一些圆锥曲线相关的几何性质，不一定要求都要掌握，但要做到知道.