基于多自由度的小波包滚动轴承故障诊断方法
姜锐红
(上海电机学院 机械学院,上海 201306)
基于多自由度的小波包滚动轴承故障诊断方法
姜锐红
(上海电机学院 机械学院,上海 201306)
快速谱峭度图是滚动轴承故障诊断的有效方法,然而,该方法有可能将最佳频带分割到不同区域,造成对故障信息的识别能力不足,并且对随机冲击噪声的免疫力较弱。根据滚动轴承故障激发多个固有频率的特点以及平均降噪原理,提出多自由度小波包诊断方法,选取适当数量的小波包子带信号,将所选子带信号的频谱平均处理,充分利用信号的有用信息,增强了对白噪声及随机冲击噪声的免疫力。对滚动轴承故障仿真信号及实测信号分别应用快速有限冲击响应(FIR),谱峭度方法,小波包谱峭度方法以及多自由度小波包诊断方法的对比分析,表明多自由度小波包诊断方法对白噪声及随机冲击噪声具有更强的免疫力,验证了该方法的有效性及实用性。
多自由度; 小波包; 滚动轴承; 故障诊断
滚动轴承是旋转机械中最常用的零部件之一。滚动轴承寿命离散,定期检测更换制度存在极大的安全隐患,或者会造成浪费。因此,对滚动轴承进行有效的状态监测与故障诊断在电力、冶金、化工等行业中有着重要的意义[1]。
滚动轴承发生故障时,激发轴承系统的多个固有振动频率。这些固有频率分布广泛,是由轴承故障引起周期性振动,调制于所激发的固有频率形成调幅信号。为了提取轴承故障信息,大量文献对解调方法做了研究工作[2-5]。选取监测信号中某段包含轴承故障信息最强的子带信号进行包络解调的方法是其中之一[6-9]。文献[10-11]中通过短时傅里叶变换,计算得到对应所有不同带宽的谱峭度图,峭度最大值所对应的(f,Δf)(中心频率,带宽)即为包含滚动轴承故障信息的最佳位置。然而,计算量令人无法忍受,不可能实现实时监测。文献[12]中提出基于有限冲击响应(Finite Impulse Response, FIR)滤波器的二进、三进网格划分多级滤波器组的快速谱峭度算法。在此基础上,文献[13-14]中研究了基于小波包的快速谱峭度方法,文献[15]中研究了基于Morlet小波的谱峭度方法,对滚动轴承故障诊断具有良好的效果。
由于滚动轴承激发的固有频率范围广,以及快速谱峭度方法逐层频率等分的滤波特点,快速谱峭度方法有可能将包含轴承故障信息最强的窄带信号分割在不同的频率段,从而削弱了故障信息。此外,随机冲击信息较强时,会对滚动轴承有用信息的提取造成干扰。针对上述不足,本文提出基于多自由度的小波包诊断方法,深入研究了其原理及算法实施,并将其应用于滚动轴承故障仿真信号与实测信号的处理。
1 多自由度小波包诊断原理
1.1 快速谱峭度原理
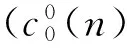

图1 低通/高通滤波示意Fig.1 Low pass/high pass filtering
(1)
基于FIR的快速谱峭度图诊断方法相当于指定一系列子带信号的频率中心与带宽,因此,最终搜索到的最优频带与实际信号中故障信息最强的频带往往会有一定的偏差。当信号的实际最佳频带中心落在预先划分的频带边缘时,FIR的快速谱峭度图选取的最佳频带至少将一半有用故障信息丢失,对噪声的免疫力会明显降低。由于小波包二叉树的频率混叠特点,将FIR滤波器改为小波包滤波器,有助于提高快速谱峭度方法对滚动轴承故障的诊断性能。然而,由于滚动轴承故障信息广泛分布于较宽频域范围,只选择一个窄带子信号提取故障特征显然没有充分利用有用信息。
1.2 平均降噪原理
信号的时间平均可以将周期性信息从噪声干扰中提取出。由于滚动轴承故障信息所在频率范围广,对快速谱峭度方法,即使是没有被选到的子带信号,其中也会包含故障信息。因此,可将故障特征频率视为以每层子带宽度为周期的周期信息,而其他频率成分即为噪声:
Xevelope(f)=Xfeature(f)+Xnoise(f)
(2)
式中,Xevelope(f)为子带信号包络谱;Xfeature(f)为滚动轴承故障特征频率幅值;Xnoise(f)为特征频率之外的噪声频率幅值。
若相同强度的故障信息分布在每个窄带中,并且各个子带所加入的白噪声强度也相同,将所有子带信号的包络谱累加结果为
Xevelope(sum)(f)=
(3)
式中,M为窄带个数;Xevelope(sum)(f)为M个窄带包络谱累加和,将其平均,可得平均包络谱为
(4)

上述平均降噪原理可由图2进一步说明。由于对滚动轴承的诊断只需获取信号中的故障特征频率,也即信号中相应的特征频率值是否高于噪声信息,故将累加和序列做归一化处理,以便与原始序列作对比。图2(a)中,时间序列4无明显峰值,其余3个序列均仅包含一个峰值(可视为故障特征信息),累加和序列全部捕捉到3个峰值,并且相对原序列中的峰值更加突出。图2(b)中,4个原始序列均包含且至少包含1个峰值,累加和序列将原序列中的所有峰值全部捕捉到。在原4个序列中不只存在于1个序列中的同时间峰值经过累加和处理后更加突出。因此,累加和处理有助于增强存在于多个序列中的弱峰值。以上各原始序列的峰值分布特点与滚动轴承故障信号窄带包络谱中的特征频率分布一致。因此,将谱峭度图中多个子带包络解调谱累加可以起到降噪作用。此外,由图2(b)也得知,对于并非存在于所有原始序列中的峰值,累加处理后会被削弱。在实际诊断应用中,对累加和过程应加入合理的限制条件,以免将有用信息弱化。

图2 时间平均降噪原理Fig.2 Principle of time average de-noise
2 多自由度小波包诊断方法实施
滚动轴承点蚀故障引起的冲击可视为随机点过程,各个冲击发生时刻为随机变量并且独立同分布。由故障冲击激起轴承系统一个以上的固有频率的模型称为多自由度故障模型。图3(a)的滚动轴承多自由度外圈故障仿真信号中,由轴承故障引起系统3个固有频率:fc(1)=3.5kHz,fc(2)=7.5kHz,fc(3)=9kHz,采样频率fs=25kHz,由故障引起的冲击到达周期近似为1/125s,波动范围为1%。图3(b)为上述仿真信号的频谱。
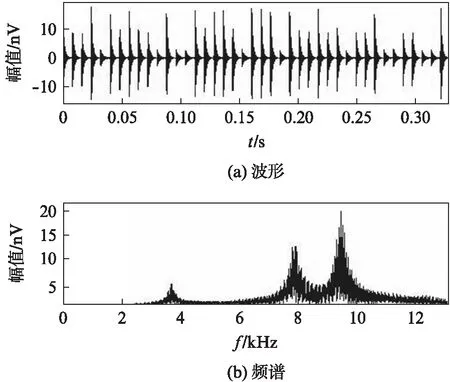
图3 多自由度滚动轴承外圈故障仿真信号波形及频谱Fig.3 Simulating waveform and frequency spectrum of the rolling bearing outer fault based on multi-degree of freedom
多自由度小波包(MDF-WP)诊断方法的具体实施过程如图4所示。将信号进行小波包分解后,指定欲累加的小波包层,将各小波包子带系数绝对值进行傅里叶变换,得到该层各子带信号的广义检波包络谱为
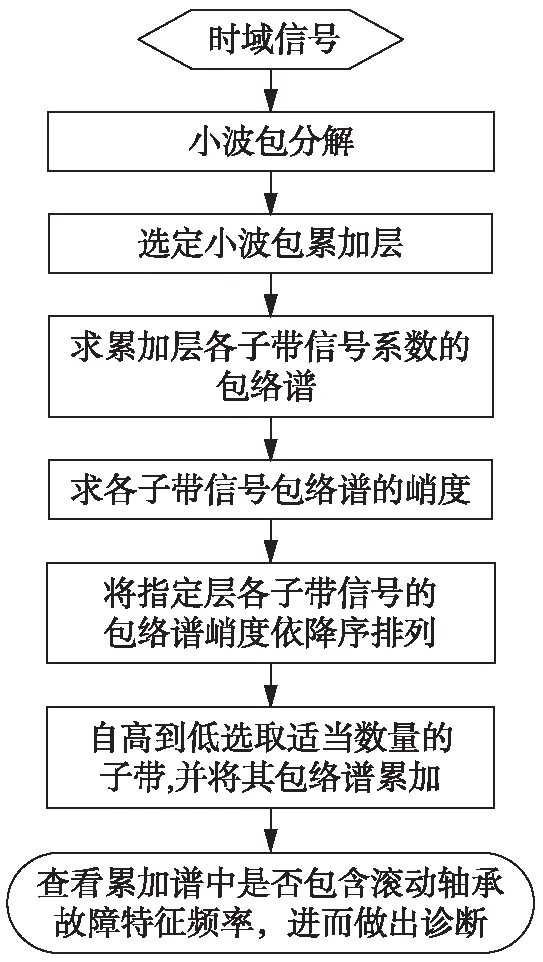
图4 多自由度小波包滚动轴承故障诊断流程Fig.4 Fault diagnosis flow for rolling bearing based on MDF-WP
(5)
式中,e-j2πtf为傅里叶变换因子;i为指定层中参与累加的子频带位置;Xi(f)为各子频带信号的包络解调谱。
将各子带包络解调谱累加得到包络谱之和为
(6)
式中,M取值不超过2k-1;X(f)是否包含故障特征频率即为滚动轴承诊断的依据。
3 仿真信号诊断
为评估多自由度小波包方法对滚动轴承故障的诊断性能,将图3轴承外圈故障仿真信号中加入随机冲击信息,图5给出了加入随机冲击信息的滚动轴承故障信号的波形和频谱图,在 10kHz 附近出现能量较高的峰值,该频率并非轴承系统的固有频率,可以判断此处的较高能量是由所加入的随机冲击引起。

图5 加入随机冲击的外圈故障仿真信号波形及频谱Fig.5 Simulation waveform and frequency spectrum of outer fault with random impact
分别应用FIR快速谱峭度方法与小波包谱峭度方法对上述信号进行处理,得到如图6的FIR谱峭度图和小波包谱峭度图。图6(a)的FIR谱峭度图中,虚线矩形框内最亮部分峭度值最大,为所选最优频带,中心频率 11458.33Hz,频带宽度为2083.33Hz。由轴承系统的固有频率值可以判断所选最优频带的较高能量与滚动轴承故障无关。图6(b)的小波包谱峭度图中,由虚线矩形框确定的最优频带中心为 7031.33Hz,频带宽度1562.5Hz。该频带将轴承故障激起的一个共振频率7.5kHz包含在内。

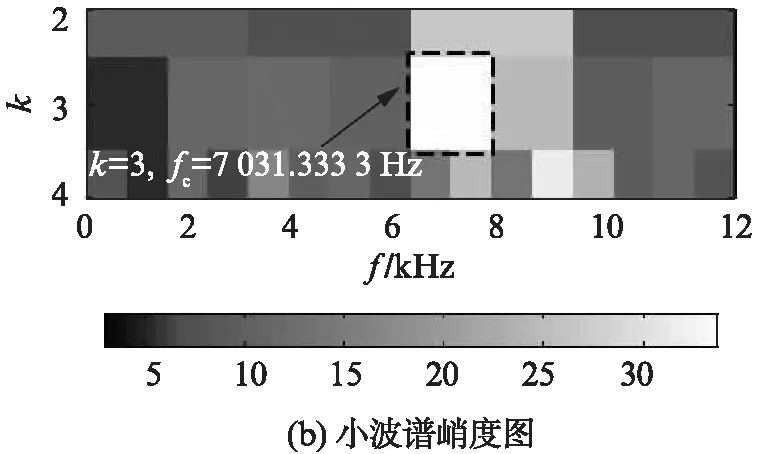
图6 加入随机冲击的外圈故障仿真信号FIR和 小波包谱峭度图Fig.6 FIR kurtogram and WP kurtogram for outer fault signal with random impact
图7(a)给出了图6(a)中最优频带子信号的平方包络谱,其中轴承故障特征频率没有突出显现,这与之前判断该处较高能量由随机冲击引起相吻合,表明所加入的随机冲击噪声干扰了FIR谱峭度方法对轴承故障信息的识别。图7(b)给出了图6(b)对应的小波包谱峭度图所选最优频带信号的包络解调谱,其中具有较高峰值的125.2Hz对应仿真信号的故障特征频率,表明小波包谱峭度方法对随机冲击噪声的抗干扰能力强于FIR谱峭度方法。图7(c)为小波包第5层中包络谱峭度最大的2个子带信号包络谱累加和,其中轴承故障特征频率及其2倍频均显著,同时其他频率成分较图7(b)得到更好抑制。小波包第5层中全部子带信号的包络解调谱累加和如图7(d)所示,其中除故障特征频率之外的干扰频率成分幅值有所增大,故障信息突出程度较图7(c)略差,但相对于图7(b),故障特征信息明显增强。这表明对子带有选择性地累加,对故障特征提取有较大影响。
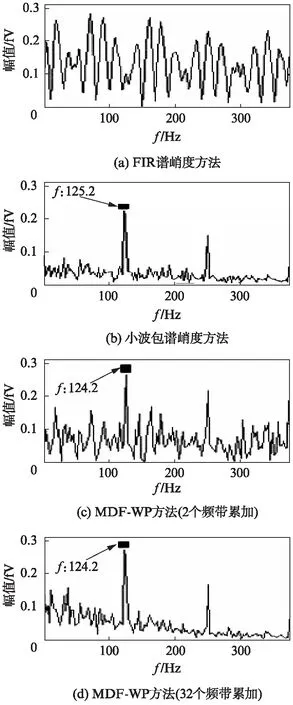
图7 3种方法对仿真信号的分析对比Fig.7 Comparison and analysis of three methods
4 实测诊断应用
实测轴承故障信号由凯斯西储大学的轴承数据中心提供[16]。实验中,轴承外圈固定于轴承座,内圈与转轴固定,转速为1774r·min-1(对应转频29.6Hz),根据轴承参数计算得其外圈故障特征频率为106Hz,保持架公转频率为11.78Hz。该外圈故障信号的时域波形与频谱如图8所示。
图9为故障信号的FIR谱峭度图,矩形虚线框内中心频率位于5.5kHz,频带宽度为1kHz的最亮部分为所选最优频带。
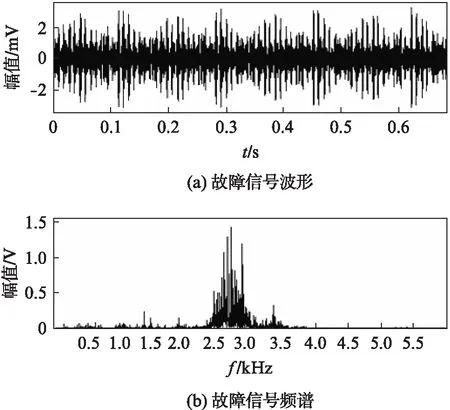
图8 实测滚动轴承外圈故障波形及频谱图Fig.8 Measured waveform and spectrum of the rolling bearing outer fault
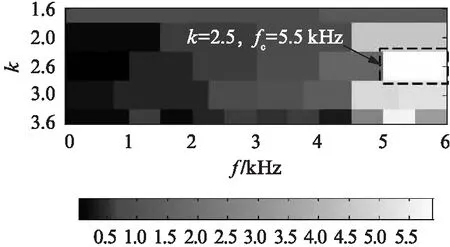
图9 实测滚动轴承外圈故障FIR谱峭度图Fig.9 FIR kurtogram of measured signal of the rolling bearing outer fault
图10为Coiflet3小波包谱峭度图,其中虚线矩形框中最亮部分中心频率为3187.5Hz,频带宽度375Hz。

图10 实测滚动轴承外圈故障小波包谱峭度图Fig.10 WP kurtogram of measured signal of the rolling bearing outer fault
图11(a)给出了图9矩形虚线框内对应的频带的包络谱,其中包含了故障特征频率、轴转频及保持架转频,由FIR谱峭度图成功检测到轴承外圈故障的所有有用信息。此外,还有较多不相干频率不利于辨识有用信息。图11(b)给出了图10中矩形虚线框中子带的包络解调谱,其中有一跳跃峰值对应轴承外圈故障特征频率,但整体表现为较平滑的连续谱线,不足以凭该频带包络解调谱识别滚动轴承故障。由此可见单一最优频带对滚动轴承故障识别具有局限性。图11(c)为小波包第4层子带排序后的第1个窄带信号包络解调谱,其中外圈特征频率与其2倍频清晰显现。此外,比较明显的内圈转频29.28Hz为轴承正常工作状态可能出现的频率。

图11 3种方法实测诊断效果对比Fig.11 Comparison and analysis of three methods
图11(c)中外圈故障特征频率及其2倍频显著突出,转轴频率较为突出,而保持架转频及其倍频消失,也即与故障相关的有用信息得到很好地强化。图11(d)将小波包第4层中所有子带包络谱累加,结果捕捉到轴承故障有用信息,外圈故障特征频率及其2倍频较图11(a)清晰简洁,其余大部分有用信息之外的频率幅值得到明显抑制。可见,3种方法中,多自由度小波包方法对滚动轴承的故障识别能力最强。
5 结 论
将FIR滤波器以小波包滤波器取代,结合时间平均降噪技术,取多个子带信号包络解调谱累加和的MDF-WP诊断方法,相比FIR快速谱峭度方法及小波包谱峭度方法,通过包络谱累加可以将分布在不同频率区间的滚动轴承故障特征信息全部利用,提高了信噪比,增强了对滚动轴承的故障识别能力。
当滚动轴承故障信号中混入非高斯性随机冲击信息干扰时,由于其很强的峭度特征,使得FIR快速谱峭度方法及小波包谱峭度方法难以捕捉到滚动轴承故障有用信息。然而,由于随机冲击的包络谱不具有周期性的特征频率,MDF-WP方法可以将随机分布的冲击信息有效抑制,对其具有更强的免疫力。
对累加子带数量的选取仍为该方法需要进一步研究的内容,如何利用人工智能自动选取合适的子带数量将是下一步的研究目标。
[1] RANDALL R B,ANTONI J.Rolling element bearing diagnostics-a tutorial[J].Mechanical Systems and Signal Processing,2011,25(2):485-520.
[2] 石林锁,沈金伟,张亚洲,等.基于AR模型和谱峭度法的滚动轴承故障诊断[J].振动与冲击,2011,30(12):257-260.
[3] 石林锁,张亚洲,米文鹏.基于WVD的谱峭度法在轴承故障诊断中的应用[J].振动、测试与诊断,2011,31(1):27-31.
[4] 张亚洲,石林锁,秦亮.基于谱峭度法和自适应遗传算法的轴承故障诊断[J].轴承,2010(3):40-43.
[5] 蔡艳平,李艾华,石林锁,等.基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J].振动与冲击,2011,30(2):167-172.
[6] 苏文胜,王奉涛,张志新,等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击,2010,29(3):18-21.
[7] 程军圣,杨怡,杨宇.基于LMD的谱峭度方法在齿轮故障诊断中的应用[J].振动与冲击,2012(18):20-23.
[8] 郭瑜,郑华文,高艳,等.基于谱峭度的滚动轴承包络分析[J].振动、测试与诊断,2011,31(4):517-521.
[9] 刘亭伟,郭瑜,李斌,等.基于谱峭度的滚动轴承故障包络阶比跟踪分析[J].振动与冲击,2012,31(17):149-153.
[10] ANTONI J,The spectral kurtosis:A useful tool for characterising non-stationary signals[J].Mechanical Systems and Signal Processing,2006,20(2):282-307.
[11] ANTONI J,RANDALL R B.The spcetral kurtosis:application to the vibratory surveillance and diagnostics of rotating machines[J].Mechanical Systems and Signal Processing,2006,20(2):308-331.
[12] ANTONI J.Fast computation of the kurtogram for the detection of transient faults[J].Mechanical Systems and Signal Processing,2007,21(1):108-124.
[13] LEI Y,LIN J,HE Z,et al.Application of an improved kurtogram method for fault diagnosis of rolling element bearings[J].Mechanical Systems and Signal Processing,2011,25(5):1738-1749.
[14] 丁康,黄志东,林慧斌.一种谱峭度和Morlet小波的滚动轴承微弱故障诊断方法[J].振动工程学报,2014,27(1):128-135.
[15] JIANG R,LIU S,TANG Y,et al.A novel method of fault diagnosis for rolling element bearings based on the accumulated envelope spectrum of the wavelet packet[J].Journal of Vibration and Control,2013,21(8):1580-1593.
[16] Case Western Reserve University Bearing Data Center.Ball bearing test data for normal and faulty bearings [EB/OL].(2004-04-05)[2016-09-10].http:∥www.eecs.case.edu/laboratory/bearing/download.htm.
Fault Diagnosis for Rolling Element Bearings Based on Multi-Degree ofFreedom and Wavelet Packet
JIANG Ruihong
(School of Mechanical Engineering, Shanghai Dianji University, Shanghai 201306, China)
The spectral kurtogram is effective for rolling bearings fault diagnosis. However, its performance is inadequate to identify fault information since it is possible to divide the optimal frequency-band into different bands. In addition, the method is vulnerable to random impulse noise. As rolling bearings fault can excite vibrations of multiple frequencies, a diagnosis method of multi-degree of freedom-wavelet packet (MDF-WP) is proposed using the average de-noising principle. Reasonable sub-band signals of the WP are selected, and their frequency spectrums are processed by average de-noising. Useful information in the signal is fully used so that immunity to white noise and random impulse noise is improved. Bearing fault simulation signals and the measured signals of the rolling bearings are processed by three methods:fast FIR spectral kurtogram, wavelet packet spectral kurtogram and the proposed MDF-WP method. The results show that the MDF-WP method is more robust to white noise and random impulse noise, verifying its validity and practicability.
multi-degree of freedom(MDF); wavelet packet(WP); rolling element bearing; fault diagnosis
2016-10-18
国家自然科学基金面上项目基金资助(51575331);国家自然科学青年基金项目资助(61603238);上海高校青年教师培养计划项目资助(A1-5701-16-014-07)
姜锐红(1973-),女,讲师,博士,主要研究方向为机电设备故障诊断,E-mail:jiangruihong2@163.com
2095-0020(2016)06-0318-07
TH 133.33
A

