切换系统的研究综述

刘永慧

(上海电机学院 电气学院，上海 201306)

切换系统的研究综述

刘永慧

(上海电机学院 电气学院，上海 201306)

对切换系统的研究进行了阐述。从系统建模、稳定性分析、镇定、能控和能观性4个方面介绍了切换系统的研究现状，并重点介绍了公共Lyapunov函数、多Lyapunov函数等稳定性分析方法。最后，对目前的研究进行了展望。

混合动态系统; 切换系统; 稳定性; 公共Lyapunov函数; 多Lyapunov函数

混合动态系统是既包含离散事件动态系统，又包含连续变量动态系统，且两者相互作用的系统。[1]。由于混合动态系统包含了离散事件和连续时间变量，在理论研究上面临极大的挑战。此外，实际工程系统中所有涉及逻辑决策和连续控制的系统，如机器人系统[2]、化工控制过程[3]等都可以转化为混合动态系统，因此，混合动态系统一直是控制界研究的热点。

切换系统是一类典型的混合动态系统，它由一族子系统(子模态)以及描述它们之间联系的逻辑规则构成。其中，逻辑规则又称为切换信号。切换系统的本质是切换，切换思想在日常生活中应用广泛。继电器在闭合、断开两种模式间变换以及齿轮变速器档位的变化都是通过切换实现的[1]。实际上，多控制器系统本身就是一个典型的切换系统。

切换系统自被提出以来就一直是控制界的研究热点。近年来，切换系统在稳定性分析、镇定等方面得到了很多有益的结论[4-6]。由于切换系统的应用背景非常广泛，故其备受关注；很多实际系统，如电动机系统[7]、航天控制系统[8]等，因环境变化会呈现出不同的模态。切换系统的动态性能也非常复杂，当所有子系统都稳定时，设计出的切换信号不一定能保证整个系统稳定，即整体性能不等于各个模态性能的简单叠加，甚至会有截然不同的性能。

本文系统地总结了切换系统的发展并对其进行了评论。从系统建模、稳定性分析、镇定、能控性和能观性4个方面介绍了切换系统的发展，并对目前的研究进行了展望。

1 切换系统模型描述

切换系统中的连续子系统用微分方程给出，离散子系统用差分方程给出。一般情况下，连续非线性切换系统表示为

(1)

式中，fσ(t)(x(t))为任意非线性函数；x(t)为系统的状态；σ(t):[0,∞)→Γ={1,2,…,s}为切换信号，当σ(t)在指标集Γ={1,2,…,s}中取定时，系统将运行相应的子系统。

切换信号主要包含以下几类[9]:①σ(t)是任意的切换信号，通常是一个分段右连续常值函数；②σ(t)是受限的切换信号，即它是可设计的切换信号(通常依赖于状态或时间)；③σ(t)是随机的(通常满足Markov过程)。

一般情况下，连续线性切换系统表示为

(2)

式中，Aσ(t)为系统的状态矩阵。

离散切换系统的数学模型可根据连续时间的模型类似地给出。

本文给出2个切换系统及其应用的例子。

例1带切换的简单RC电路。

图2为一个简单的相移(Resistance-Capacitance,RC)电路的电路图。电路中含有切换开关S，其作用是选择电路中的电阻R1和R2；E1和E2是两个恒压源；iC为通过电容器C的电流。当开关S在1和2之间切换时，电路方程可以用如下的切换系统来描述:

(3)

图1 带切换的简单RC电路Fig.1 Simple RC circuit with a switch

例2三罐系统[3]。

图2为三罐系统的示意图。液体由罐1流出，经过切换开关流向罐2或罐3。

假设罐1的流入速度为v，罐1、2、3的液面高度分别为x1、x2、x3，流出速度分别为k1、k2、k3，且液体高度与流速成线性关系。当开关打到罐2时，液面高度可描述为

(4)

当开关打到罐3时,液面高度变换为

(5)

由上述例子可见，系统进行切换使得系统的动态性能更加丰富，这为复杂系统的研究提供了很好的研究思路。

2 研究现状

2.1 稳定性分析

由于子系统不断地进行切换，故切换系统的稳定性分析与一般系统的稳定性分析方法有所不同。切换系统的稳定性分析更复杂，主要表现在以下方面:① 子系统均稳定的切换系统，在某些切换信号作用下也会失稳；② 子系统均不稳定的切换系统，通过设计合适的切换信号也可能实现系统稳定。

可见，切换系统的稳定性分析主要建立在切换信号的选取上。文献[10]中将其稳定性分析归结为以下问题:① 任意的切换信号下，切换系统的稳定性；② 受限的切换信号下，切换系统的稳定性；③ 构造一个切换信号，使得切换系统稳定。

对于第①个问题，研究的思路是将传统的Lyapunov稳定性理论推广到切换系统，得到的方法主要有变分法、公共Lyapunov方法等。

(1) 变分法。文献[11]中采用变分法研究了含有2个子系统的线性切换系统在任意切换信号作用下系统的稳定性。变分法的核心思想是寻找切换系统中最不稳定的切换信号。若切换系统在最不稳定的切换信号下是稳定的，则对于任意的切换信号，该系统必然稳定，其中，求解最不稳定的切换信号实际上是一个优化问题求解过程。

(2) 公共Lyapunov函数方法。文献[12]中提出了公共Lyapunov函数方法，给出切换系统全局一致渐近稳定(即对于任意的切换信号，系统均渐进稳定)的条件，即切换系统存在公共Lyapunov函数。

之后，学者们对于公共Lyapunov函数存在的代数条件进行了研究。文献[13]中证明了如果系统矩阵Ai(i∈Γ)为一组可交换的稳定矩阵，则线性切换系统存在公共二次Lyapunov函数，并给出了该函数的构造方法。文献[14]中证明了对于式(2)，若由Ai(i∈Γ)，生成的Lie代数可解，则该系统存在共同的二次Lyapunov函数。在此基础上，文献[15]中进一步将上述结论推广到非线性切换系统。

显然，上述给出的公共Lyapunov函数是切换系统稳定的充分条件。对于其必要性，文献[16]中运用向量场的理论做了进一步研究，并证明了对于线性切换系统，上述条件是一个充要条件。

(3) 多Lyapunov函数方法。切换系统的公共Lyapunov函数不易构造，学者们将构造公共Lyapunov函数列为控制系统中未解决的问题之一。因此，运用设计受限的切换信号来研究切换系统的稳定性开始受到学者们的关注，并得到了多Lyapunov函数方法(主要有驻留时间方法、平均驻留时间方法等)。

从物理角度讲，系统不稳定是由于系统能量没有被完全吸收造成的，因此，如果子系统下次被激活时的Lyapunov函数值始终小于上次被激活时的Lyapunov函数值，此时系统能量衰减，则系统稳定。基于上述思想，文献[17]中提出了多Lyapunov函数方法。多Lyapunov函数有连续和离散两种情况(见图3)。

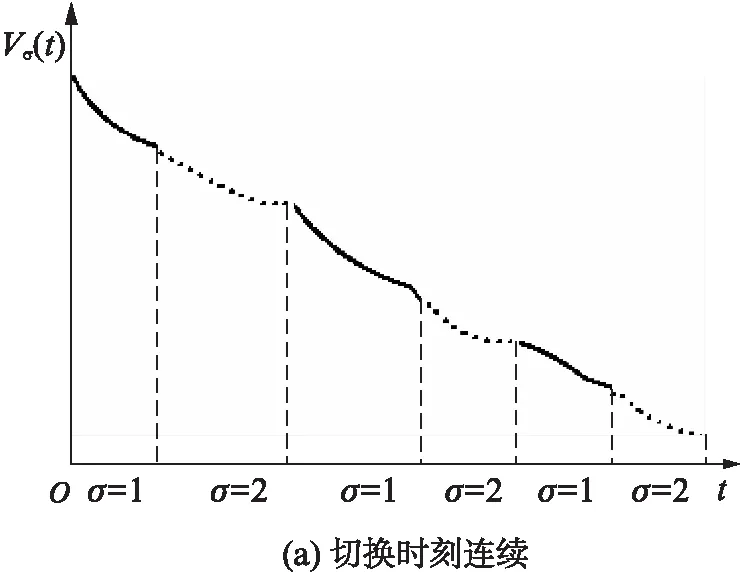
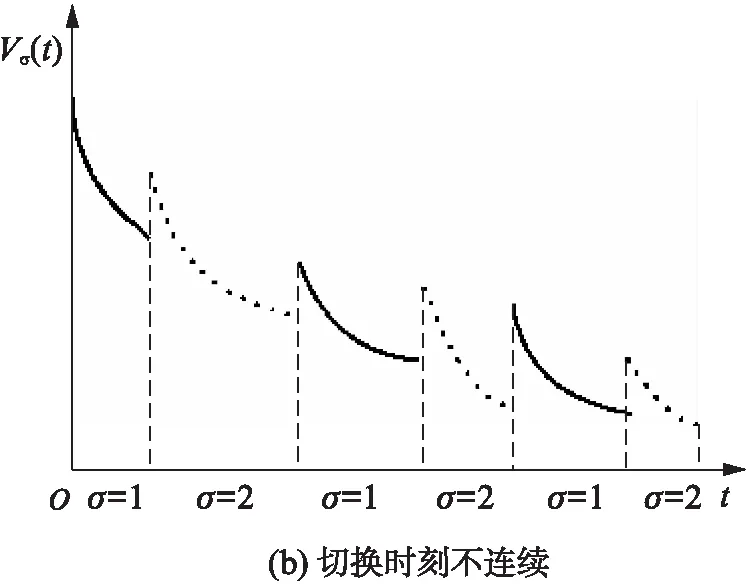
图3 多Lyapunov函数Fig.3 Multiple Lyapunov function

上述切换系统的稳定性是建立在子系统均稳定的条件下。文献[18]中将上述结论作了进一步改善，提出了类似Lyapunov函数，只需要求子系统在其运行时间段内稳定即可(见图4)。

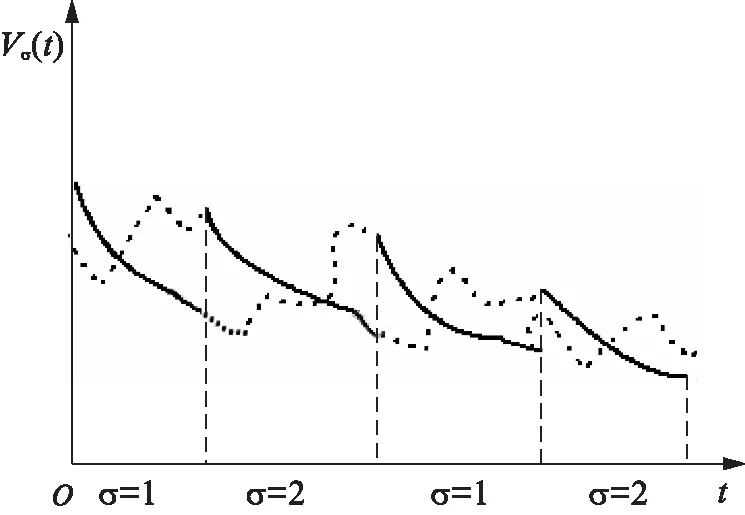
图4 类似Lyapunov函数Fig.4 Like multiple Lyapunov function

(4) 驻留时间方法。当系统切换到不稳定的子系统时，停留在该子系统的时间过长或切换到该系统过于频繁，都会导致系统不稳定。因此，当停留在稳定子系统内的时间足够长时，可抵消系统能量的增长，且当系统的切换不太频繁(即慢切换)[19]时，即可保证切换系统稳定。

基于上述慢切换的思想和多Lyapunov函数稳定性理论，Morse[20]提出了驻留时间方法，证明了对于系统式(2)，若存在多Lyapunov函数Vi(x(t)):Rn→R，i∈Γ，两个K∞函数α1、α2和参数λ0>0，其中，K∞函数是一类特殊函数，该类函数单调递增，且函数的初始值为0。参数μ>0满足:

(6)

且驻留时间(即系统连续两次切换之间的间隔时间)τσ满足:

τσ>lnμ/(2λ0)

(7)

则系统全局渐近稳定。

在此基础上，文献[19]中进一步提出了平均驻留时间方法。近年来，驻留时间方法得到了进一步推广和应用:文献[21]中证明了对于含有不稳定子系统的切换系统，驻留时间方法仍然适用，并且给出了系统指数稳定的条件。文献[22]中进一步分析了当所有子系统均不稳定时系统的稳定性。平均驻留时间方法在非线性切换系统[23]以及时滞切换系统[24]的研究中也得到了广泛应用。此外，文献[25]中采用临界驻留时间方法，分析了线性切换系统的稳定性。对于线性切换系统，文献[26]中给出了最小驻留时间的估计方法。

(5) 依赖于状态的切换信号。受限的切换信号可分为时间域限制和状态空间限制。文献[27]中首次提出了设计状态受限的切换信号，通过将整个状态空间分成不同的区域Ωi，i∈Γ，并在不同的区域内选取适当的Lyapunov函数，保证系统能量函数衰减。

文献[28]中设计了基于投影变换的切换信号

(8)

式中，Qi为正定矩阵。

将切换系统式(3)的稳定性分析转化为一个优化问题求解。文献[29]中进一步提出了面向路径的状态反馈型切换信号，不再限制划分的状态区域和要求系统子模态的个数相同。文献[30]中采用多面体类似Lyapunov函数方法，设计了依赖状态的切换信号，分析了系统的稳定性，但是该方法在应用时不易验证。

多Lyapunov函数方法是切换系统稳定性分析中常用的方法，但是需要实时地比较函数值，这给应用带来了不便。文献[31]中进一步定义了持续稳定性和逐点镇定，讨论了系统在固定切换信号和受限切换信号两种情况下，初始值在一定范围波动时系统的稳定性。

2.2 镇定问题

设计切换信号使得切换系统稳定本质上属于切换系统的镇定问题。切换系统的镇定控制可分为3类，即设计合适的切换信号、设计合适的切换控制器以及同时设计合适的切换信号和切换控制器。

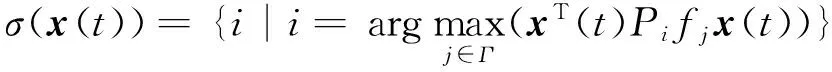
(9)

显然，与文献[32]比较，文献[33]中的结论更具一般性。

(2) 控制器的设计。当切换信号固定或是任意的切换信号时，只需设计切换控制器以确保系统稳定。对于任意的切换信号，文献[34]中采用极点配置方法分析了系统的镇定问题。文献[35]中通过对系统进行变换，研究了一类单输入平面切换系统在任意切换信号下的反馈控制。给定依赖状态的切换信号，文献[36]中设计了饱和控制器，研究了切换系统的镇定控制。

(3) 同时设计切换信号和控制器。主要研究切换系统的镇定问题。文献[37]中基于系统的结构特点，构造了合适的切换律和控制器，分析了平面切换线性系统的镇定问题。有些研究是在特殊的切换信号下(如最小投影方法和平均驻留时间方法等)，分析系统的镇定问题。其中，文献[38-39]中分别运用平均驻留时间方法和和最小投影方法设计切换信号，分析了系统的反馈镇定问题。

2.3 能控性和能观性

目前，关于切换系统的能控性、能观性的研究大都针对线性切换系统展开的[40-43]。其中，文献[40]中定义了线性周期切换系统的能观性，并给出了能观性的充要条件；由对偶原理进一步得到了系统能控性的充要条件。在此基础上，文献[41]中进一步给出了一般线性切换系统能控性的充要条件。对于离散时间线性周期切换系统，文献[42]中进一步给出了其能控性和能观性的充要条件。之后，文献[44-45]中对于切换系统的能控能观性进行了深入研究，给出了切换系统可控集的定义，得到了能控性的Gram判据，给出了线性切换系统可控性的充要条件，并证明了可控性与可观性之间的对偶性。文献[46]中进一步研究了线性切换系统可控的代数条件，证明了若Gram矩阵是行满秩的，则线性切换可控。文献[47]中分析了同时含有连续离散子系统的线性切换系统的可控、可观性，并得到了其可控、可观的充要条件。

综上所述，国内外学者对于切换系统的稳定性分析及镇定控制已经展开了较为深入的研究。值得注意的是，对于切换系统其他方面的研究，如鲁棒控制[48-49]、容错控制[50-52]、优化控制[53-55]等方面也得到了很多有意义的成果。

3 展 望

本文对切换系统的研究进行了阐述并进行了评论。切换系统应用广泛，仍有许多问题尚未解决，现就今后的研究方向做简单的论述。

(1) 切换系统稳定性分析中，如何构造公共Lyapunov函数，仍是尚待解决的问题。此外，如何给出新的稳定性定义以及便于验证的方法有待进一步解决。

(2) 对于时间受限的切换信号，如何给出驻留时间的非保守估计是新的研究方向。

(3) 目前得到的稳定性分析方法大多是针对一般的切换系统，如何将上述结论推广到复杂的切换系统，如随机切换系统、Markovian跳变系统等有待进一步解决。

(4) 近年来，切换系统的研究中出现了很多优化问题，如双线性不等式求解等问题，如何给出这些问题的算法将是一个新的研究方向。此外，对于实际切换系统，如何选择最优的切换时刻以及切换信号，使系统的性能达到最优，这无疑是一个具有深远应用前景的研究方向。

(5) 切换控制与智能控制方法相结合。目前，切换控制与模糊控制、神经网络控制等智能控制方法相结合的成果并不多，将智能控制方法与切换控制相结合必定能取得很多有意义的成果。

(6) 切换系统在各领域的应用还值得深入研究。切换系统理论在飞行控制、网络控制、电力电子系统等领域的应用还需要深入研究。引入了切换思想后，上述系统可看作一个切换系统，切换系统在稳定性分析方面的成果可以应用到系统的稳定性分析中。

[1] 莫以为,萧德云.混合动态系统及其应用综述[J].控制理论与应用,2002,19(1):1-8.

[2] HISKENS I A, Stability of hybrid system limit cycles:Application to compass gait biped robot[C]∥Proceeding of the 40th IEEE Conference on Decision and Control. Orlando, Florida, USA:IEEE,2001:774-779.

[3] LENNARTSON B, TITTUS M，EGARDT M, et al, Hybrid systems in process control[J]. IEEE Control Systems,1996，16(5):45-56.

[4] CHENG Danzhan, GUO Lei, LIN Yuandan. Stabilization of switched linear systems[J]. IEEE Transactions on Automatic Control,2005,50(5):661-666.

[5] SHORTEN R, WIRTH F, MASON O, et al. Stability criteria for switched and hybird systems[J]. SIAM Review,2007,49(4):545-592.

[6] LIN Hai, ANTSAKLIS P J. Stability and stabilizability of switched linear systems:A survey of recent results[J]. IEEE Transactions on Automatic Control,2009,54(2):308-322.

[7] SANDERS S R, VERGHESE G C. Lyapunov-based control for switched power converters[J]. IEEE Transactions on Power Electronics,1992,7(1):17-24.

[8] LIBERZON D. Switching in Systems and Control[M]. Birkhäuser Boston:[S.n.],2003.

[9] 程代展,郭宇骞.切换系统进展[J].控制理论与应用,2005,22(6):954-960.

[10] LIBERZON D, MORSE A S. Basic problems in stability and design of switched systems[J]. IEEE Control Systems,1999,19(5):59-70.

[11] MARGALIOT M. Stability analysis of switched systems using variational principles:An introduction[J]. Automatica,2006,42(12):2059-2077.

[12] DOGRUEL M, OZGUNER U. Stability of a set of matrices:An application to hybrid systems[C]∥Proceedings of 1995 IEEE International Symposium on Intelligent Control. [S.l.]:IEEE,1995:59-64.

[13] NARENDRA K S, BALAKRISHNAN J A. A common Lyapunov function for stable LTI systems with commuting A-matrices[J]. IEEE Transactions on Automatic Control,1994,39(12):2469-2471.

[14] LIHERZON D, HESPANHA J P, MORSE A S. Stability of switched systems:a Lie algebraic condition[J]. Systems & Control Letters,1999,37(3):117-122.

[15] MARGALIOTA M, LIBERZON D. Lie-algebraic stability conditions for nonlinear switched systems and differential inclusions[J]. Systems & Control Letters,2006,55(1):8-16.

[16] DAYAWANSA W P, MARTIN C F. A converse Lyapunov theorem for a class of dynamical systems which undergo switching[J]. IEEE Transactions on Automatic Contro1,1999,44(4):751-760.

[17] BRANICKY M S. Stability of switched and hybrid systems[C]∥Proceedings of the 33rd IEEE Conference on Decision and Control. Lake Buena Vista, FL:IEEE,1994:3498-3503.

[18] BRANICKY M S. Multiple Lyapunov functions and other analysis tools for switched and hybrid systems[J]. IEEE Transactions on Automatic Control,1998,43(4):475-482.

[19] HESPANHA J P, Morse A S. Stability of switch-ed systems with average dwell-time[C]∥Proceedings of the 38th IEEE Conference on Decision and Control. Phoenix, Arizona, USA:IEEE,1999:2655-2660.

[20] MORSE A S. Supervisory control of families of linear set-point controllers-part I:Exact matching[J]. IEEE Transaction on Automatic Control,1996,41(10):1413-1431.

[21] ZHAI Guisheng, HU Bo, YASUDA K, et al. Stability analysis of switched systems with stable and unstable subsystems:An average dwell time approach[J]. International Journal of Systems Science,2001,32(8):1055-1061.

[22] XIANG Weiming, XIAO Jian. Stabilization of switched continuous-time systems with all modes unstable via dwell time switching[J]. Automatica,2014,50(3):940-945.

[23] CHATTERJEE D, LIBERZON D. On stability of randomly switched nonlinear systems[J]. IEEE Transactions on Automatic Control,2007,52(12):2390-2394.

[24] VU L, MORGANSEN K A. Stability of time-delay feedback switched linear systems[J]. IEEE Transaction on Automatic Control,2010,55(10):2385-2390.

[25] ZHANG Lijun, LI Chunwen. Critical dwell time of switched linear systems[J]. Journal of Control Theory and Applications,2006,4(4):402-408.

[26] Ni Wei, CHENG Daizhan, HU Xiaoming. Minimum dwell time for stability and stabilization of switched linear systems[C]∥Proceeding of the 7th World Congress on Intelligent Control and Automation. Chongqing:IEEE,2008:4103-4108.

[27] WICKS M A, PELETIES P, DECARLO R A. Switched controller design for the quadratic stabilization of a pair of unstable linear systems[J]. Eur-opean Journal of Control,1998,4(2):140-147.

[28] PETTERSSON S. Synthesis of switched linear systems[C]∥Proceedings of the 42nd IEEE Conference on Decision and Control. Maul, Hawail, USA:IEEE,2003:5283-5288.

[29] SUN Zhendong. Stabilizing switching design for switched linear systems:A statefeedback path-wise switching approach[J]. Automatica,2009,45(7):1708-1714.

[30] LIN Hai, ANTSAKLIS P J, Switching stabilizability for continuous-time uncertain switched linear systems[J]. IEEE Transactions on Automatic Control,2007,52(4):633-646.

[31] SUN Zhendong. Stabilizability and insensitivity of switched linear systems[J]. IEEE Transactions on Automatic Control,2004,49(7):1135-1137.

[32] COLANERI P, GEROMEL J C, ASTOLFI A. Stabilization of continuous-time switched nonlinear systems[J]. System & Control Letters,2008,57(1):95-103.

[33] HU Tingshu. MA Liqiang, LIN Zongli. Stabilization of switched systems via composite quadratic functions[J]. IEEE Transactions on Automatic Control,2008,53(11):2571-2585.

[34] WULFF K, WIRTH F, SHORTEN R. A control design method for a class of switched linear systems[J]. Automatica,2009,45(11):2592-2596.

[35] CHENG Daizhan. Stabilization of planar switched systems[J]. Systems & Control Letters,2004,51(2):79-88.

[36] LU Liang, LIN Zongli. A switching anti-windup design using multiple Lyapunov functions[J]. IEEE Transactions on Automatic Control,2010,55(1):142-148.

[37] HU Qingxi, CHENG Daizhan. Stabilizer of planar switched linear systems[J]. System & Control Letters,2008,57(10):876-879.

[38] SUN X M, ZHAO J, WANG W. State feedback control for discrete delay systems with controller failures based on average dwell-time method[J]. IET Control Theory and Applications,2008,2(2):126-132.

[39] GEROMEL J C, DEAECTO G S. Switched state feedback control for continuous-time uncertain systems[J]. IEEE Transaction on Automatic Control,2009,45(2):593-597.

[40] EZZINE J, HADDAD A H. Controllability and observability of hybrid systems[J]. International Journal of Control,1989,49(6):2045-2055.

[41] 杨振宇.递阶混合动态系统[D].北京：北京航天航空大学,1997.

[42] SOH C B. Controllability and observability of periodic hybrid interval systems[J]. International Journal of Systems Science,2000,31(12):1563-1571.

[43] 谢广明,郑大钟.一类混合动态系统的能控性和能观性研究[J].控制理论与应用,2002,19(1):139-142.

[44] XIE Guangming, WANG Long. Controllability and stabilizability of switched linear systems[J]. Systems & Control Letter,2003,48(2):135-155.

[45] XIE Guangming, WANG L. Necessary and sufficient conditions for controllability and observability of switched impulsive control systems[J]. IEEE Transactions on Automatic Control,2004,49(6):960-966.

[46] YANG Zhenyu．An algebraic approach towards the controllability of controlled switching linear hybrid systems[J]. Automatica，2002,38(7):1221-1228.

[47] LIU C, LI C, LI C. Controllability and observability of switched linear systems with continuous-time and discrete-time subsystems[J]. IET Control Theory & Applications,2012,6(6):855-863.

[48] 聂宏,赵军.一类不确定切换组合系统的分散H∞鲁棒镇定[J].自动化学报,2004,30(4):635-640.

[49] 孙文安,赵军.基于LMIs的不确定线性切换系统H∞鲁棒控制[J].控制与决策,2005,20(6):650-655.

[50] NGUYEN A, DAMBRINE M, LAUBER J. Lyapunov-based robust control design for a class of switch-ing non-linear systems subject to input saturation:Application to engine control[J]. IET Control Theory & Applications,2014,8(17):1789-1802.

[51] LI Lili, ZHAO Jun, DIMIROVSKI G M. Observer-based reliable exponential stabilization andH∞control for switched systems with faulty actuators:An average dwell time approach[J]. Nonlinear Analysis:Hybrid Systems,2011,5(3):479-491.

[52] LIU Yonghui, NIU Yuangang, LAM J, et al. Sliding mode control for uncertain switched systems with partial actuator faults[J]. Asian Journal of Control,2014,16(6):1779-1788.

[53] LIU Yonghui, NIU Yuangang，ZOU Yuanyuan. Adaptive sliding mode reliable control for switched systems with actuator degradation[J]. IET Control Theory & Applications,2015,9(8):1197-1204.

[54] 费树岷,王泽宁,冯纯伯.一类开关系统的开关控制策略优化设计[J].自动化学报,2001,27(2):247-251.

[55] XU Xuping, ANTSAKLIS P J. Optimal control of switched systems based on parameterization of the switching instants[J]. IEEE Transactions on Automatic Control,2004,49(1):2-16.

Review of Switched System Research

LIU Yonghui

(School of Electrical Engineering, Shanghai Dianji University, Shanghai 201306, China)

This paper studies switched systems. From modeling, stability analysis, stabilization and controllability, and observability of switched systems, the current status of switched system research is discussed. The stability analysis methods include common Lyapunov functions and multiple Lyapunov functions. Prospects for the research are given.

hybrid dynamic system; switched systems; stability; common Lyapunov functions; multiple Lyapunov functions

2016-05-06

上海市高校青年教师培养计划项目资助(15U02)

刘永慧(1986-)，女，讲师，博士，主要研究方向为切换系统、滑模变结构控制，E-mail:liuyh@sdju.edu.cn

2095-0020(2016)06-0330-08

TP 273； TP 13

A