论初中数学教学中反思习惯的养成

赵 勇●

江苏省宜兴市丁蜀镇东坡中学(214221)



论初中数学教学中反思习惯的养成

赵 勇●

江苏省宜兴市丁蜀镇东坡中学(214221)

在初中数学教学中，教师通过有效的观察、回顾和自我监控等手段，可以发现教学过程中的缺陷和不足，也即创设有效的反思机会，培养学生的反思习惯，可以帮助学生在初中数学的学习过程中，认真回顾自己的数学思维形成过程，并进入到抽象概括的理性思维阶段，提升学生的数学思维深度和广度.

初中数学；反思；习惯

在初中数学的认知活动之中，由于数学知识的严谨推理特性、数学活动的探究特性，对于初中生而言，难于一次性全面把握数学知识的本质，它需要初中学生在具备初步的认知活动的前提下，多次重复地加以思考和反思，并对自己的数学学习进行深入的分析、反思和调整，洞察初中数学活动的本质内涵和规律，从而完成数学学习任务，全面提升自己的数学学习能力.

一、通过数学提纲的预设，培养学生的反思习惯和能力

在初中数学新知识的传授过程中，预习是一种极为有效的学习方式，学生通过课前预习，增强数学学习的积极性，在主动参与的过程中提出数学问题，并在反复的反思训练中，促使学生学会预习，提升数学自主学习能力.

例如：在苏教版初中数学《一元二次方程的解法》的教学中，教师可以通过预习提纲的方式，培养学生在数学预习中的反思习惯.

《一元二次方程的解法》一课的预习提纲：

1.回顾既学知识：(1)一元二次方程的概念是什么？它的普通形式如何表达？(2)一个数的平方根如何表达？

2.数学合作探究与反思.探究问题(1)：如果x2=2，那么x=____.探究问题(2)：如果2x2=1，那么x=____.反思(1)：在探究问题(1)中，如果已知x2=p(p≥0)的条件，那么如何求出它的平方根；反思(2)：如果二次项系数不为1，那么可以用直接开平方法解方程吗？如何解？

3.预习讨论.(1)解方程2x2-3=0；(2)解方程4(x-1)2-9=0.

二、通过对数学解题过程的反思，培养学生的反思习惯

在初中数学学习过程中，学生的数学思维品质需要在不断的反思活动中生成，通过对数学解题过程的反思，可以增进学生对于数学知识理解的深度和广度，从而培养数学学习思维和数学学习能力.

例如：在初中数学解直角三角形的应用例题之后，可以引导学生对例题的解题过程进行反思，并引导学生在反思的过程中，进行类比分析、归纳推理、总结概括，从而寻求数学解题过程的规律性和特点.在教师的引导之下，学生进入对例题解题的反思，并反思得出以下结论：(1)这几个例题都与方程知识相关联；(2)要运用锐角三角函数的概念知识，加以分析和理解；(3)要运用几何知识.这些结论归结为同一种解题思维模式，即：将实际问题几何化、几何问题方程化，在这个解题思维模式反思之下，学生的解题思路更为清晰，也提升了学生的不断探索和创新的精神.

三、通过对数学解题思路的反思，培养学生的反思习惯

新课程标准注重学生的既有经验，主张将具体的实际问题加以抽象化、概括化，将其纳入数学模型之中，进行求解和应用.然而，在数学教学活动中，却急于将新知传授给学生，并加以练习巩固，对于新知识的获取思路、获取路径和过程却缺少反思.为此，我们要注重培养学生的反思习惯，要通过对新知识的习得方式、习得过程、习得路径，加以反思，从而掌握数学学习方法.

例如：在初中数学“菱形面积的计算”的教学内容中，教师在引导学生进行实践活动的探索之后，得出菱形面积的公式，获得这个结论之后不要急于进入演练阶段，而要学生对公式获得的过程加以回顾和反思，要对菱形面积的计算公式重新审视，回想公式是如何一步步得出的？这样，才能使学生的数学解题思路更为清晰，更为有序，从而体悟到数学转化思维和学习方法，增强数学解题能力.

四、通过对数学解题结论的反思，培养学生的反思习惯

在初中数学解题过程之后，会得出相关的数学结论，教师要引领学生对数学解题结论进行反思，要运用数学语言对问题进行重新的描述和概括，从而提升学生的数学思维敏捷性和深度，提升数学学习能力.

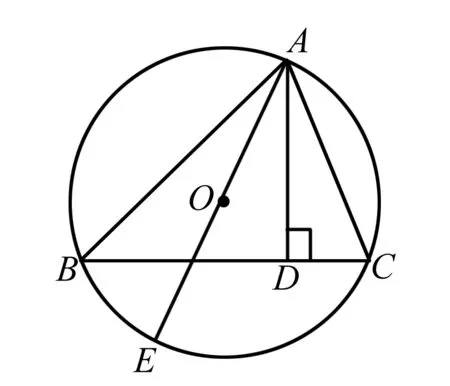
例如：在下图所示中，AD是△ABC的高，AE是△ABC外接圆的直径.求证：AB·AC=AE·AD.

在得出求证结论之后，教师引导学生进行反思，总结出这个习题可以无须画圆，这是由于任意三角形都有外接圆，而外接圆的直径是显而易见的，这样，外接圆的直径无须画出来，就可以得出求证的结论.在对问题的本质进行顿悟之后，学生可以用数学语言对其加以概括，即：任意三角形的两边，第三边上的高与外接圆直径的数值中知道任意三个量，即可以求出第四个量，在对其进行反思之后，可以得到任意三角形外接圆直径的特殊求解方法，从而实现数学知识的正向迁移.

[1] 李显显.数学教学学生实践能力培养思考[J]. 中华少年，2016(25)

[2] 王先国.浅谈数学解证题中逻辑思维能力的培养[J]. 现代阅读(教育版)，2013(03)

G632

B

1008-0333(2016)35-0035-01