几何变换思想——初中几何问题的活性酶

吴秀明●

江苏省苏州高新区实验初级中学 (215000)



几何变换思想
——初中几何问题的活性酶

吴秀明●

江苏省苏州高新区实验初级中学 (215000)

随着核心素养的提出，为了更好地培养学生的空间观念和几何直觉，在初中数学课堂教学中潜移默化地渗透几何变换思想，能有效地有助于学生强大的几何知识网络的形成，培养学生的创新意识，提高了学生解决现实问题的能力.

数学思维能力；几何变换；全等变换；相似变换

早在1872年，德国数学家克莱因(F·Klein)在题为《近代几何学研究的比较评述》的演讲中，提出了用变换观点来看待几何学，后来称之为“Erlanger rro-gramm”(爱尔兰根纲领).几何变换思想就成为初等几何的现代数学思想，他认为每一种几何都由一种变换群所刻画,每一种几何学要做的实际上就是寻求图形在该变换群的作用下保持不变的性质,一个几何的子几何是在原变换群的子群作用下的不变量.

新课改后，几何的变换成为“空间与几何”的三大内容之一；同时在近几年的中考题中，图形的变换也已成为命题热点.而几何变换思想为这一类问题提供了一种十分重要的思维方式.

几何变换思想包含了两个思想：一是变换的思想，二是不变的量.几何变换思想帮助我们运用运动、变化的观点去研究不变量之间的关系，使几何问题变得更形象、更直观，多角度培养学生的空间观念和几何直觉，培养学生的观察力、想象力和创造力.

几何变换是指把一个图形F1变换成另一个图形F2的方法.几何变换的类别很多，其中全等变换(合同变换)、相似变换等都是最基本的几何变换.

把只改变图形的位置，不改变图形的形状和大小的变换称作全等变换(合同变换).

把改变图形本身的大小，不改变图形的形状(保留线段间的比例关系)的变换称作相似变换.

把改变图形的形状但保持面积不变的情况下的变换称作等积变换.

下面通过几个例题谈谈如何通过上述几种基本的几何变换更好更快地找到解决问题的方法，感受初中几何中动静结合的美妙.

一、全等变换

全等变换是整个初中几何中最基础的一种变换.翻折、平移、旋转是常见的全等变换.

1.翻折变换

把一个图形沿着某条直线翻折180°后形成新的图形，这样的图形运动称为翻折.翻折的实质是轴对称，有时翻折变换也称轴对称变换.

例1 如图1-1，牧童在A处放马，其家在B处，A、B到河岸l的距离分别为AC=1km，BD=3km，且CD=3km．牧童从A处将马牵到河边饮水后再回家，试问在何处饮水，所走路程最短，请在图中画出饮水的位置．并求出图中的最短路程．

分析 如果A、B两点在直线l的异侧，则根据“两点之间，线段最短”很容易就能找到所要求出的点，但图1-1中A、B两点却在直线l的同侧，此时可想到翻折变换，运用运动的观点把同侧的点转化到异侧.如图1-2，作出点A关于直线l的对称点A′，连接A′B，此时A′B与河岸CD交点为点E，则点E就是饮水的位置，可得最短路程为A′B的距离.再根据勾股定理，构造Rt△A′FB，易得，A′B=5km，即最短路程AE+EB=5km.

例2A，B，C三个村庄在一条东西走向的公路沿线，如图2-1，AB=2km，BC=3km，在B村的正北方向有一个D村，测得∠ADC=45°．今将△ACD区域规划为开发区，除其中4km2的水塘外，均作为建筑或绿化用地，试求这个开发区的建筑及绿化用地的面积是多少？

分析 如图2-2所示，将△ABD，△BCD分别沿着DA，DC作翻折变换，得△AFD，△ECD，延长EC，FA交于点G，易证四边形DFGE是正方形.设BD=x，在Rt△AGC中运用勾股定理，易得x=6，∴S△ADC=15km2.∴开发区的建筑及绿化用地的面积是15-4=11 km2.

在此例中本来以为“山穷水尽疑无路”了，可抓住45°和垂直两个条件，运用翻折变换后，构造了一个正方形，真是“柳暗花明又一村”啊！让人直感叹翻折变换的奇妙无穷.

利用翻折构造轴对称图形，能使已知条件和所需要的结论之间产生关系，从而使令人迷茫的问题立刻有豁然开朗的感觉.

我们在题目中出现角平分线、垂直平分线或等腰三角形等这样的轴对称条件时，可考虑翻折变换.

2.平移变换

一个图形沿着某一个方向移动一定的距离，这样的图形运动称为平移.平移变换的实质是图形上的每一个点都沿着相同的方向，平移了相同的距离，平移的方向和平移的距离是平移的二要素.

例3 有一条河，两岸有A、B两地，要设计一条道路，并垂直于河岸架一座桥.如何设计才能使A、B路线最短？

分析 虽然A、B两点在河两侧，但连接AB的线段不垂直于河岸．由于桥MN是垂直于河岸的，所以问题的关键在于使AM+BN最短，但AM与BN未连起来，要用线段公理就要想办法使M与N重合起来.利用平移变换可以实现这一目的，将一些线段进行转化，即用与它相等的线段替代，从而转化成两点之间线段最短的问题．

如图3-2，过点A作AA′⊥l，且AA′等于河宽，连接A′B交直线n于点N，作NM⊥m于点M，则MN就是桥的位置.同时平移变换也经常会将线段平移形成平行四边形，从而可以用平行四边形的性质.初中阶段很多重要的添辅助线方法，如中线倍长、梯形中平移腰，平移对角线等都是对平移变换的巧妙运用.

3.旋转变换

一个图形绕着一个定点朝着某个方向转过一定的角度，这样的图形运动称为旋转.旋转由旋转中心、旋转方向、旋转角度决定.

例4 已知，如图4-1，正△ABC内有一点P，PA=6，PB=8，PC=10．求：

(1)∠APB的度数；

(2)△ABC的面积．

分析 图中PA、PB、PC三边的值正好是一组勾股数，但又相对比较分散，没有构成三角形，而整幅图形又是以等边三角形为背景的，不妨考虑实施旋转变换.将△ABP绕点A逆时针旋转60°得△ACP1，易证△APP1是等边三角形，△PP1C是直角三角形，从而不仅把分散的线段集中了起来，并且转化成了我们比较熟悉的图形，得到∠APB=∠AP1B=90°+60°=150°，使问题(1)得到了解决.对于问题(2)，求等边三角形的面积，乍一看似乎无从下手，但已有基本图形等边△APP1和直角△PP1C的面积是可求的，故用同一思想继续旋转(如图4-3)，形成一个六边形，该六边形是由三个面积可求的小等边三角形和三个直角三角形构成，同时该六边形又是等边△ABC面积的两倍，从而可使问题得到化解.

由此，旋转变换能将相对比较分散的条件集中在一个我们所熟悉的图形之中，以解决问题.

通常， 当图形中以等边三角形或等腰直角三角形、 正方形等为背景时，可考虑实施旋转角为60°或90°的旋转变换.

二、相似变换

图形的相似变换是指由一个图形变换到另一个图形时，保持形状不变(大小方向和位置可变).图形相似变换后对应线段都扩大(或缩小)相同的倍数，这个数叫相似比.显然，当相似比为1时，相似变换就是合同变换．

例5 已知，如图5-1，平行四边形ABCD中，对角线AC、BD相交于点O，E是AB延长线上一点，连结OE交BC于点F．若AB=a，BC=b，BE=c，求BF．

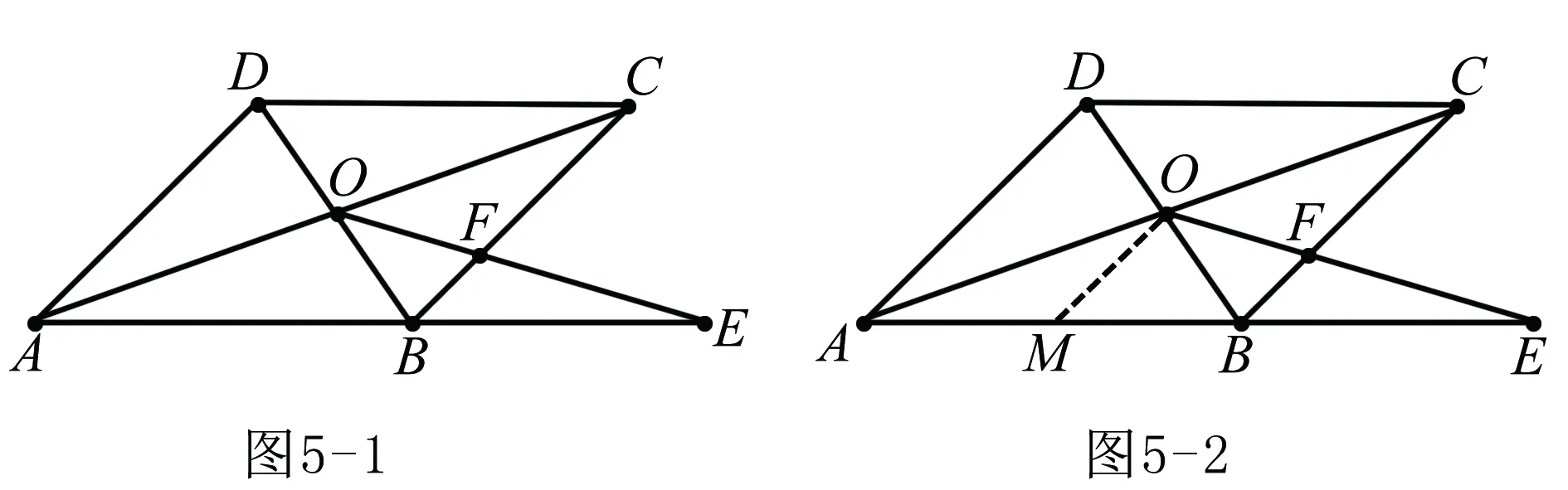
当问题设计与线段长度、平行(或共线)有关系时，可考虑进行相似变换，试将一些线段分别变换到其位似形中的对应线段，使相互关系明朗化.一般，利用位似变换解题时如需作辅助线，往往是作一些平行线.相似在几何计算线段的长度，角的度数，证明线段成比例，角相等等方面具有广泛的应用.

几何变换是一种奇妙的变换，还贯穿在定义、定理、推论、作图等几何教学过程中，是研究几何的有力工具，是平面几何的活性酶，是一种数学的思维艺术.平时在教学过程中我们应潜移默化地渗透几何变换思想，有助于学生强大的几何知识网络的形成，培养了学生的创新意识，提高了学生解决现实问题的能力，发展了学生的形象思维与抽象思维.

[1]王林全.从美国高中课程标准看几何教改新趋势[J].中学数学月刊,2015.

[2]陈培培.数学试验，让课堂更精彩——从一节“平移翻折旋转”课谈起[J].中学数学,2016.

G632

B

1008-0333(2016)35-0021-02