等效思维在初中物理解题中的应用研究
叶敬凯●
江苏省宿迁市宿豫区陆集中心学校(223804)
等效思维在初中物理解题中的应用研究
叶敬凯●
江苏省宿迁市宿豫区陆集中心学校(223804)
为了保证教学质量,教师应该注重恰当初中物理教学方法的使用.就解题过程教学而言,等效思维法的融入能够快速实现解题目的.本文从等效思维法的概念入手,对等效思维在初中物理解题中的应用进行研究.
等效思维;初中物理;解题;应用
一、等效替代法在初中物理解题中的应用如果学生遇到的物理问题较为复杂,可以利用等效替代法对复杂问题进行有效简化.这里以下列例题为例,对等效替代法的应用进行研究.

如图1所示,现有等臂杠杆AB,该杠杆的两端分别被同一种圆板固定住.目前已知杠杆A端圆板半径为r,OA之间的距离为2r.且该圆板上含有一个r1半径的圆,r是r1的2倍.为了保证该等臂杠杆的平衡状态,应该将B端圆板的半径控制为多少?
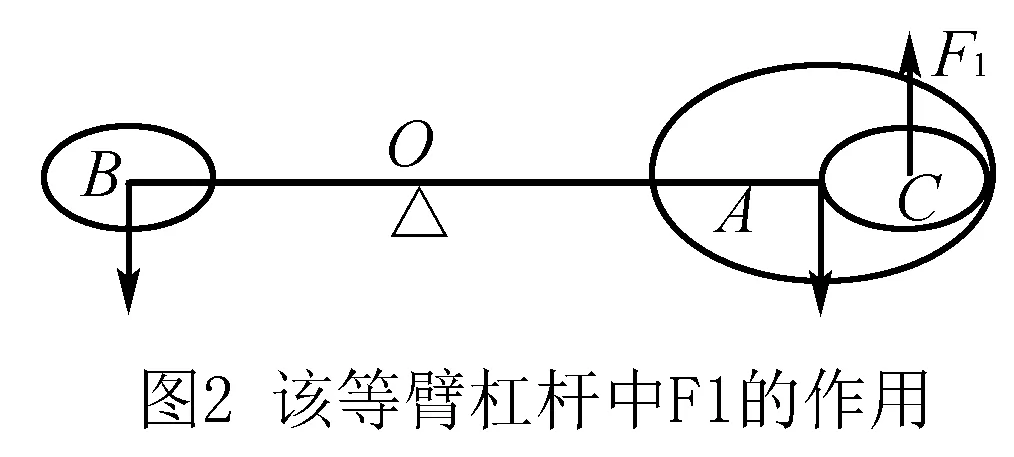
当学生遇到这种问题时,通常会利用计算等臂杠杆A端圆板重心的方式获得B端圆板的实际半径.这种计算方法涉及的计算步骤较多,因此可以利用等效替代法对该问题进行合理简化.题目中指出,A端圆板中有一个半径为0.5r的圆,可以利用等效思维将这个圆看成:一个大小与该圆重力相等的力F1以垂直向上的方向作用于该圆的孔心中,如图2所示.在这种情况下,学生可以根据力矩平衡条件快速将B端圆板的半径计算出来.
二、等效假设法在初中物理解题中的应用
可以通过等效假设法的应用将物理题目中的隐蔽问题表示出来,进而实现解题难度的降低.这里以某例题为例,对该方法的应用进行研究.

如图3所示,该电路中的内电阻和电源电动势分别为r和ε.其中,R2为变阻器,R1则是定值电阻.如果需要保证变阻器R2所消耗的电功率为最大值,其电阻以及电功率最大值分别为多少?
应用等效假设方法,可以将图3中虚线圈出来的部分看成一个电源.在这种情况下,R1不再是该电路中的定值电阻,而是新电源的内阻.因此,可以将计算出该电路的等效电阻r1为:r1=R1r/(r+R1)其等效电动势为唯一外电阻R2断开情况下虚线的两端电压,该等效电动势ε=R1/(r+R1).根据题目中的要求,当R2与r1的电阻值相等时,其消耗的电功率处于最大值状态.
三、等效变换法在初中物理解题中的应用
学生在解答初中物理题目的过程中,问题中给出的电路通常较为复杂,在这种情况下,可以利用等效变换法,将其简化成较为简单的方式进行计算.这里以某例题为例,对等效变换法的应用进行研究.

如图4所示,该电路图中的内电阻较小,可以忽略不计.其电源电动势为12V,除R1之外的电阻阻值全部为r.已知该电路消耗的功率为20W,R1为9Ω.如果利用电阻为3Ω的R2替换原本的R1,则该电路消耗的总功率会变为多少?
学生在解答该问题过程中面临的主要困难是:其很容易被电路中的多个电阻所困扰.因此,可以利用等效变换法,将该电路中除R1之外的所有电阻看成一个大电阻,该电阻与R1之间的关系为并联关系,利用该方法可以将图4中的电路图简化为图5中的电路图.在这种情况下,可以计算出该电路所消耗的总功率,总功率p的计算公式如下:p=[ε2(R0+R1)]/R0R1.将题目中的已知条件代入该公式,可以计算出R0的值为36Ω.当R1变为3Ω时,电路消耗的总功率将变为52W.与原本的计算方法相比,等效变换法的应用实现了复杂问题的简化,这种方法的应用有利于学生实际物理问题解决能力的提升.
为了更好地解决这些物理问题,学生可以根据实际的物理问题,应用等效假设、等效变换等相关等效思维.这种方法的使用可以将原本较为复杂的物理问题转化为简单模式,进而提升学生的问题解答速度和解答质量.
[1]姬鸣亚. 等效思维在初中物理解题中的合理运用[J]. 中学物理,2016,10:94-95.
[2]叶新. 等效思维在初中物理解题中的运用[J]. 理科考试研究,2016,12:58.
G
B
1008-0333(2016)35-0055-01

