二次函数的经典题型——二次函数图象与系数之间关系的应用

王 荣●

黑龙江省大庆市登峰学校(163112)



二次函数的经典题型
——二次函数图象与系数之间关系的应用

王 荣●

黑龙江省大庆市登峰学校(163112)

二次函数是初中数学重要的知识之一.二次函数中有许多经典题型，下面通过一个例题的解答对这种特殊题型的解题方法及步骤做一归纳总结，如果同学们以后遇到这种典型题，就迎刃而解了，供同学们参考.知识点清单：

【二次函数图象与系数】

一般式y=ax2+bx+c(a≠0)

①二次项系数a决定抛物线的开口方向和大小

② 一次项系数b和二次项系数a共同决定对称轴的位置

当a与b同号时(即ab>0)，对称轴在y轴左边； 当a与b异号时(即ab<0)，对称轴在y轴右边．(简称：左同右异)

③ 常数项c决定抛物线与y轴交点

④ 抛物线与x轴交点个数

Δ=b2-4ac>0时，抛物线与x轴有2个交点；Δ=b2-4ac=0时，抛物线与x轴有1个交点；Δ=b2-4ac<0时，抛物线与x轴没有交点．

例 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，下列结论: ①a+b+c<0，②a0，④abc>0，其中正确的序号是____.

解析 第一步：a、b、c各自的符号

抛物线开口向下，所以a<0.根据对称轴在y轴的左侧(左同右异)，所以b<0.抛物线与y轴交点在y轴正半轴上，所以c>0.故④正确.

第三步：特殊点代值

当x=1时，a+b+c>0；当x=-1时，a-b+c>0；当x=2时，4a+2b+c<0；

当x=-2时，4a-2b+c=0等，故①错误.

第四步：推导(根据选项来)

方法：一看，二解，三代入

一看：看选项中少哪个字母；

二解：从已得到的等式中解出这个字母；

三代入：将解出的字母代入得到的每一个式子中，直到得出要找的式子.

下列我们来推导③选项.

一看：③2a+c>0没有字母b，

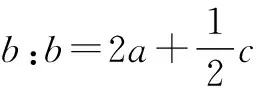
由此，例1的答案为②③④.(此题选项③是难点)

小结：这一类二次函数经典题型的解题步骤：

第一步：a、b、c各自的符号；

第二步：对称轴的位置或范围并化简；

第三步：特殊点代值；

第四步：推导(根据选项来)：一看，二解，三代入.

G632

B

1008-0333(2016)35-0006-01