几何概型教学中的理解学生

官运和

（广东韶关学院数学与统计学院 512005）

几何概型是中学数学的一项重要的教学内容，由于是新增内容等原因，也是较难把握的教学内容.它的前置知识是概率的统计定义和等可能概念以及古典概型，是第二类等可能概率模型，它把等可能事件的概念从有限延伸到无限.等可能、无限是二个极其抽象的概念，为教学增加了难度.教学概率的目的是学习用数学方法去研究不确定现象的规律，培养学生用科学态度、辩证思维、随机观念去观察、分析、研究客观世界.

学生主体，教师主导，即教学的双主性是被大家认可的，认可归认可，但落实并不尽人意.怎么落实，说教可能会空洞，不妨结合中学几何概型的教学就双主性的基础问题——理解学生来展开讨论，谈点思考.

1 理解学生，理解学生思维的跨度

对于大众教育而不是精英教育，我们鼓励低起点，小跨度，注重思维的连贯性，走进思维的最近发展区，一步一步往前走，走得踏实有力.从古典概型到几何概型的过渡来考查学生的思维跨度.

从一些教学比赛的数学课以及公开课来看，较多老师对教学几何概型设计的教学流程是：知识回顾（或复习旧知：古典概型）——创设情景、引入新课——讲解新课（几何概型）——概念深化（列表对比古典概型与几何概型）——典型例题（分长度、角度、面积和体积四种情形）——课堂检测——课堂小结——课后作业，其中的创设情景、引入新课的问题是下面二题或类似题：

题1已知A=[1，8]，从A中任意取出一个整数a，求a≤4的概率.

题2已知A=[1，8]，从A中任意取出一个实数a，求a≤4的概率.

即先应用古典概型的方法解题1，接着给出几何概型的方法解题2，由题2解答抽象概括归纳几何概型概念的定义，然后就古典概型与几何概型的特点加以列表比较，然后用例题分长度、角度、面积和体积等情形加强几何概型的应用，等等，这样的教学设计看上去也没什么问题，也符合教学法的要求，有概念的形成、概念的比较、概念的深化、概念的应用等过程，但总感觉还是少了什么，或对部分学生来说还是有点不易接受，题1与题2的外在形式有很多的相似，但解法有本质的区别，没有思维上的连接，而是另辟蹊径，形成了思维跨度.

我们来看另一个设计的引例：

例1不透明的袋子中装有大小完全相同的16个小球，其中含12个白球，4个黑球，随机在袋中摸出一球，求摸出黑球的概率.

例2如图一，有一个由16块大小相同的正方形地板铺成地面的房间，其中有12块白地板，4块黑地板，小虫在地面上随意自由爬动，求小虫爬在黑地板上的概率.

图一

图二

图三

如果“面积比”意境还没出来，进一步给出下面的题目：

例3如图二，把四块黑地板移在中间位置，其它条件不变，求小虫爬在黑地板上的概率.

例4如图三所示，铺一块兰色圆地板，其余为白地板，其它条件不变，求小虫爬在兰色地板上的概率.

总结一下上面引例，例1是古典概型的问题，其它的都是几何概型的问题，从例1出发，到后面的例题，这样实现了思维的无缝对接，同时也实现了由古典概型到几何概型的过渡，实现了从有限到无限的过渡，为深入学习几何概型打下了基础，做到了低起点，小跨度，甚至是无跨度，注重思维的连贯性，走进思维的最近发展区，给学生新知识“不难”的感觉.

这里也告诉我们，古典概型和几何概型虽然是有区别的，也是紧密联系的，强调区别的同时也要注重联系，两种概型的概率其实质是统一的“比式”，事件A的测度/基本事件的总测度，因为中学生没有测度论的知识储备，因此我们避开“测度”的概念，采用“几何量”这样直观的说法，明确长度、角度、面积、体积就是几何量，那么这个比式就是个数/总个数、长度/总长度、面积/总面积、体积/总体积.

2 理解学生，理解学生思维的难度

上面已说了几何概型的概率其实质是“比式”，基本事件的几何量的比例，其中的基本事件的一个重要条件是等可能性，在概率空间中，基本事件是最原始、最小的、不可再分的事件[1]，在解决具体问题的时候，具有等可能性的原始基本事件好找，因为题目必须明确给出，但往往要将原始基本事件作等价描述，那么问题就来了，与具有等可能性的原始基本事件成一一映射的新描述的基本事件还具有等可能性吗？数学教科书经常用“一一映射”定义“等价”，文[2]给出了一种应用一一对应关系的方法：“通过实数坐标建立与基本事件的一一对应关系在坐标系中用图形表示样本空间和随机事件从而用构造出的几何量度和几何概型公式求解[2]”，然而一一对应并非普适，不妨看下面的例题：

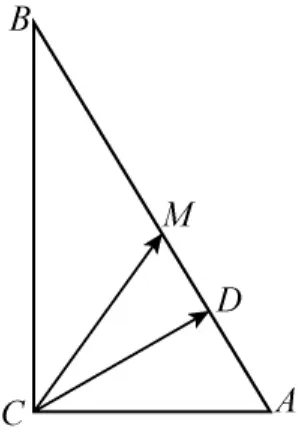
例5如图四，已知Rt△ABC中，∠A=60°，C为直角顶点，在△ABC内部过点C任意方向等可能地作一条射线CD，与线段AB交于点D，求AD≤DB的概率.

图四

图五

图六

略解：取AB的中点为M，由题意知，在△ABC内部过点C任意方向等可能地作射线CD，作出∠ACD是等可能的，则AD≤DB的概率=∠ACM/∠ACB=2/3（因为∠ACM=60°）.

思考：在△ACB内部过点C任作一条射线CD，与线段AB交于点D是唯一的，反过来，在线段AB上任取一点D与C连接得射线CD也是唯一的，因此“在△ACB内部过点C任作一条射线CD，与线段AB交于点D”与“线段AB上取点D，得射线CD”能建立一一映射，简单的说，作射线CD与AB上取点D能建立一一映射，是不是有：AD≤DB的概率=AM/AB=1/2呢？显然不是，原因是虽然作射线CD与AB上取点D能建立一一映射，但作射线是等可能的，而AB上取点不具有等可能性，也就是说一一映射并不一定传递等可能性.

等可能性在区域里面被描述为均匀分布，因此均匀分布的量经一一映射后不一定均匀分布.什么时候一一映射能传递等可能性呢，答案是：原像的相等的改变量，像的改变量也相等.本题中的角度比不等于线段比，这样的一一映射没有传递等可能性.

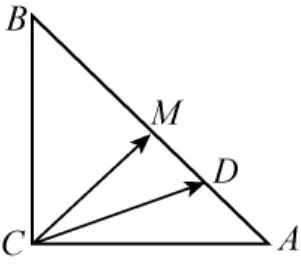
例6把例5的图形变等腰直角三角形，其它不变，情况咋样呢.即：如图五，在Rt△ABC中，AC=BC，在△ACB内部过点C任意方向等可能地作一条射线CD，与线段AB交于点D，求AD≤DB的概率.

分析：取AB的中点为M，由题意知：AD≤DB的概率=∠ACM/∠ACB=1/2.当然这时，AM/AB=1/2，是巧合，如果说AD≤DB的概率=AM/AB=1/2，答案是正确的，则过程是错误的，因为缺等可能性条件，仅是巧合而已.因为C与AB上中点连线等分∠C，但C与AB上n（n≥3）等分点连线并不等分∠C，对n=3用角平分线定理就很容易证明.

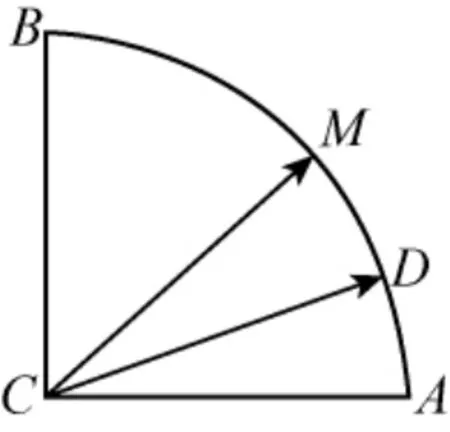
例7把例6的图形变扇形，其它不变，情况又咋样呢，即：在扇形CAB中，在扇形CAB内部过顶点C任意方向等可能地作一条射线CD，与弧AB交于点D，求弧AD≤弧DB的概率.

分析：因为弧AB上的D与C的连线任意等分角C⇔点D等分弧AB，所以当作射线CD是等可能的时候，得到在弧AB上取点D也是等可能的.因此，弧AD≤弧DB的概率=∠ACM/∠ACB=弧AM/弧AB=1/2.

学生经常信心百倍地视一些错误解法为正确解法.

3 理解学生，理解学生思维的深度

在前面的题1与题2中把A=[1，8]都改为A=（1，8），情况又咋样呢，我们知道题1的答案变了，[1，8]中含8个整数，（1，8）中只含6个整数了，而题2的答案没变，[1，8]与（1，8）的区间长度一样，就跟8与6是不同的、而∞与∞-1、∞-2没有区别是一样的道理.严格来说，一个点的长度是0，一条线的面积是0，在计算线段长度时，无论是否计算其端点，其长度不变；在计算几何区域面积或几何体的体积时，无论是否考虑其边界，区域的面积或几何体的体积不变.进一步，考虑下面的例题.

例8若A=[1，8]，则从A中任意取出一个实数a，求a=3的概率.

分析：由几何概型很容易得，a=3的概率为0.事件“从A中任意取出一个实数a，a=3”是不可能事件吗？不是不可能事件，因此，在古典概型中，基本事件有限，不可能事件⇔概率为0的事件，必然事件⇔概率为1的事件；而在几何概型中，基本事件无限多，不可能事件的概率是0，概率为0的事件不一定是不可能事件，概率为1的事件不一定是必然事件，对于无限还有很多类似的结论，这就是无限的魅力.

4 理解学生，理解学生思维的自由度

我们常说数学给的是理想化状态，是在给定条件下的结果，这没有错，但数学教学要走近学生，不能以个人意愿作为大众理解.比如：如图七，随机地向圆盘投掷飞镖，求飞镖落点位于小圆内的概率.显然命题者设定飞镖一定会击中圆盘的，但经过专业训练的世界名将都有可能脱靶，从而引起无谓的争论.

图七

在前面的例2中假如把小虫改为大象，虽然把大象看做一个点是合理的，但变成“求大象踩在黑地板上的概率”就不合常理了，设想为点的物不宜大.还有就是对于常规题要明确给出基本事件的等可能，开放题则另当别论.

5 结语

“学生主体，教师主导”这个教学的双主性是内涵丰富的话题，双主性的基础是理解学生，教学任何内容都要从理解学生做起.教学中教师经常是“教”，而不是“导”，没有教师的“导”，就不能展现学生的主体性，没有理解学生，就不会有教师的导.理解学生，就必须理解学生思维的跨度、难度、深度、自由度.对于一个随机试验，对基本事件作一一映射的描述，并不一定确保等可能性等价.