圆形包装纸最小能多小①

张培强

（江苏省徐州市第一中学 221140）

《普通高中数学课程标准（实验）》指出，高中数学课程应设立“数学探究”、“数学建模”等学习活动.教材中设立了相应的栏目，提供了一些研究性学习的素材，可以开拓学生视野，进行数学探究，提升学生分析问题、解决问题的能力.然而实施的情况并不理想，真研究少之又少.2016年9月份颁布的《中国学生发展核心素养》将“数学建模”列为数学六大核心素养之一.核心素养的提出，跳出学科知识的局限，更加从人的需要出发，为着素养的提高，为着幸福的生活.将学生能“用数学的眼光观察世界，用数学的头脑分析世界，用数学的语言表达世界”作为数学教育的终极目标.这对我们的教学活动的设计提出了更高的要求.

着眼于学生的数学建模素养的养成，选取有探究价值的素材，促进学生主动学习、主动思考、主动实践，提高学生发现问题、提出问题、分析问题、解决问题的能力.将国家课程校本化，形成以学生发展为价值取向，贴近学生生活，切实可行的问题探究课程.素材的选取至关重要，问题要入口宽，背景深，涵盖广.有时，看似一个平凡的问题，一个不经意的念头闪现，也可能会带来一场探究风暴.这不，在一次活动课间，一个学生就拿来了一个好素材（一道高三模拟题），由此引发了一场师生间的研究性学习.学生解决了疑问，教师也收获颇丰.特整理出来，与大家分享，以期抛砖引玉.

1 问题呈现

问题：有一个正四面体的棱长为3，现用一张圆形的包装纸将其完全包住（不能裁剪纸，但可以折叠），那么包装纸的最小半径为………….

此题是填空题的第8题，属于简单题，对这位学生来说应该是信手拈来的.然而他说出了自己的疑惑：这道题的答案是.把这个四面体沿三条侧棱剪开，正好展开成一个正三角形，边长为6，它的外接圆的半径正好是，所以这题应该是考展开图的.

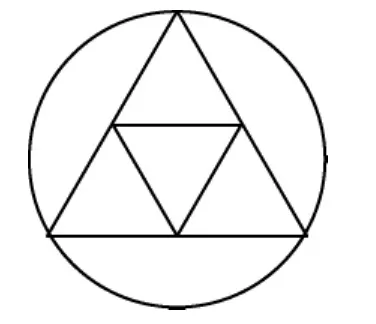
但是包装的方式可以换.可以让顶点落在圆心上，先包起三个侧面，再用余下的弓形覆盖底面三角形.如果圆刚好外接这三个三角形构成的“风扇”，那么所剩的弓形不能覆盖底面三角形.这就要把圆变大，使得弓形足够大，三个一样的弓形正好可以覆盖底面三角形.

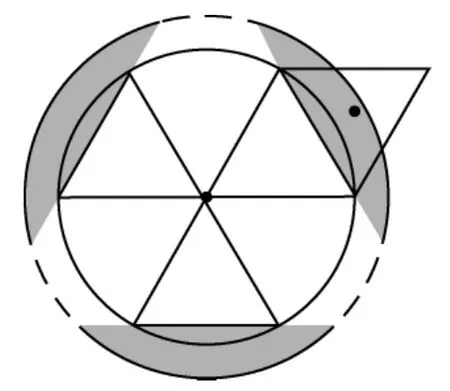
只需要每一个弓形覆盖正三角形的中心，所以圆的最小半径为正三角形高的倍，即.那么问题来了.是不是不管怎么包装，圆的最小半径都是呢？

师：你也知道这题是考展开图的，很常规的问题.那怎么又想起来换包装方式呢？

生：要是求正四面体的全面积呢，答案肯定是唯一的.但是这题要求“不能裁剪纸，但可以折叠”，所以有部分被浪费了，我就想换个包装方式，会不会少浪费点呢.

（学生的突发奇想，源自兴趣、探究的欲望.动手操作实在困难，苦思冥想而不得结果，“愤、悱”状态溢于脸庞.）

2 问题解决

师：节约是美德，找最优是数学的追求.从现在的两种包装方式的结果能否推断出圆的最小半径是，还要看这两种包装方式是否能代表一般性.第一种包装方式是将圆心放在了底面的中心上，第二种包装方式是将圆心放在了顶点，相当于反方向包装.

生：这么说，两种包装纸的大小应该是一样的.

师：感觉上是.那么还可以怎么包装呢？

（重新整理学生已经进行的探索，指出了不同包装方式的出发点，便于学生进一步建模探索.）

2.1 探寻更小

生：那就把圆心放在别的位置.因为这是个正四面体，所以只要考虑圆心在一个面内移动就可以了.刚才已经把圆心放在了正三角形的中心和顶点处，现在把圆心放在其它点处，但是这样就要偏了，要想把展开图都盖上，好像圆要变大了.

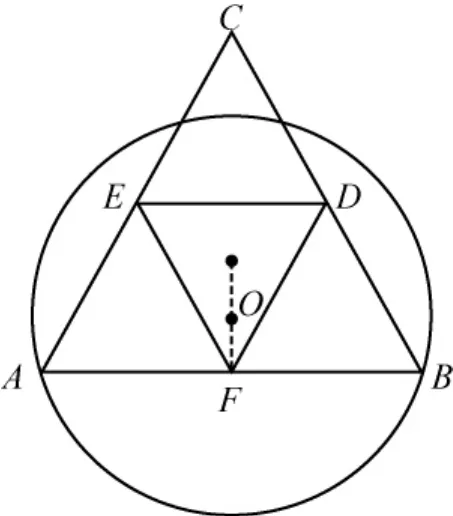
生：哦，先空出一个角，让半径变小，再用“余料”来补.那AB下方的弓形是没用的，只能用AC，BC外的弓形，我来试试.

折起来后，A，B，C重合在一起.要包上角C，相当于把边AC外的弓形绕点E旋转180度，把BC外的弓形绕点D旋转18 0度，两弧交于点P.要把△CDE完全包住，就需要点P落在圆O内.下面建系求点P坐标.

以F为原点，AB所在直线为x轴建立平面直角坐标系，则B（3，0）.设圆心O（0，m），则圆半径，所以圆弧MPC所在圆的圆心为点O关于D的对称点，所以圆O1的方程为.同理可得圆弧NPC所在圆O2的方程为.圆O1与圆O2的交点C、P都在y轴上，所以.点P要落在圆O内，则，整理得，解得.所以圆O半径，这个值大约是3.0817，果然比要小.所以原题答案错误！

2.2 产生新疑

生：这样做，圆心的位置还是特殊的.圆心除了在顶点、三角形的高上，在三角形内的其他位置上，是否还能使半径更小呢？

师：很好！要让圆心走完底面的每一点，才能最终求得最小的半径.那么继续下去，又该如何处理呢？

生：在刚才的基础上，让圆心从点O向着B移动，仍然让圆过点B，这样圆半径就比刚才的3.0817还小.但是，角A也露出来了.这样就空出两个角，可能就包不上了吧.

师：半径是小了，再看“余料”是否够用.方法应该一样.

生：是的，但不太好看了.相当于把原来关于CF对称的圆往旁边拉了一下，不对称了，所以三边之外的弓形并不一样，折起来就麻烦了.

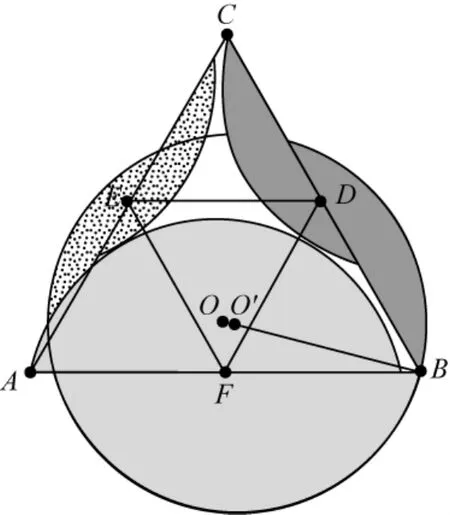
师：（通过《几何画板》动态作图验证，圆心O′移动时，找不到覆盖的情形）你能借助这个直观的结果给出解释吗？

生：因为角A和C都露出来了，所以AC外的弓形覆盖不了顶点A、C附近的部分，需要用另两边外的弓形来覆盖，也就是利用顶点B附近的“余料”.但是，O′从O到B移动的过程中，角A刚开始能被覆盖，角C左边部分始终没能被覆盖.

师：主要矛盾抓得好！首先这两个角尖得被覆盖上.从这个动态过程中，可以看出两个角尖最多有一个被覆盖.如何来准确解释这个现象呢？

生：因为BC外的弓形很小.具体来说，是点B附近的这一块覆盖不住角C.

师：《几何画板》画得太精确，所以看起来太明显了.准确还是需要用数据来说话.

生：因为∠C=60°，噢，角A、B也都是60°，所以点B所在的这部分圆要包住三个角，也就是180°，这是不可能的.

师：很好！不要让思维顺着你的目光走，那样容易“一叶障目”.综合起来看，一旦有两个角露出来，就要让圆把三个角都包上，这肯定不可能.这样不看动态过程也能立即下判断，还是思维力强啊！

生：自己动手画太模糊，《几何画板》又太明显，还是得靠想.

（学生致谢，转身准备走）

2.3 探究最小

师：这样就结束了吗？

生：还有更小的？露一个角，已经找到最小的了，露两个角不可能，露三个角就更不可能了.

师：露两个角不可能，是因为过圆上的点B作不出一个平角在圆内.那如果让点B落在圆内，不就解决问题了？

生：就是把原来的圆O拉大一点，那么点A也在圆内了，再把圆心向着点B拉，看着有更小点的可能性.我试试.

继续采用《几何画板》动态观察.可见，角A均容易被覆盖，主要是角C的覆盖，只有在O′、B′分别各自远离（或靠近）O、B时，角C好像能被覆盖上.但此时，肉眼已经无法分辨出点P是落在圆O′内，还是圆O′上，还是圆O′外.通过测量，也只能精确到小数点后5位，比较不出来.

师：它也无能为力了.看来还是要硬算.我们可以先对这个不等式消元，因为O′取在射线OB上，所以（a，b）满足方程，即b=，可代入消元.

生：试试吧（有些犹豫）.消去b，得.将看成一个整体，展开得，.，所以右边是关于a的函数，太复杂了.还要求下去么？

师：是什么类型的函数，可求吗？

生：分式函数.应该能“部分分式”成运用基本不等式的类型，可求最小值.

师：很好.类型把握得很准，不过过程有点繁琐.先用《几何画板》作图来看看吧.

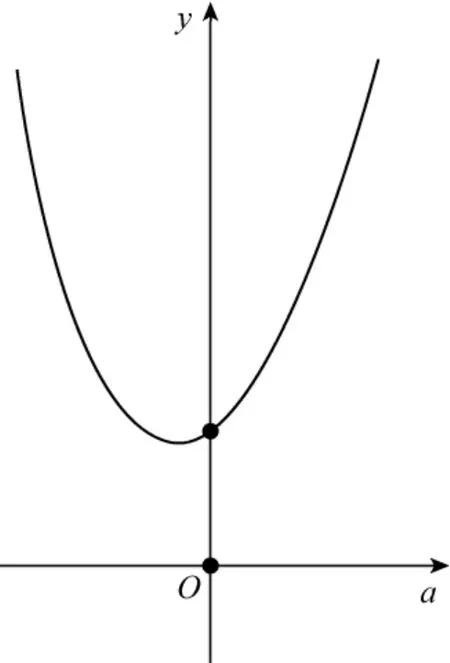
看来基本不等式用不到了.这个函数在a=0时取到最小值.

师：实际上，a=0时，O′就在点O处，这时的圆半径最小.也就说明将圆心移开点O时，圆半径都要随之变大，才能包住四面体.

3 探究感想

一个题目，几番周折，不断的生疑、释疑，追根问底，终于找到了最优解.这一段探索的历程，于学生、教师，都是不可磨灭的回忆、宝贵的财富.面对学生自主的探究活动，教师当做学生的指路人，指点迷津，使学生的学习过程成为在教师引导下的“再创造”过程.

3.1 敬畏学生做探究的热情，让数学有趣

著名数学家陈省身先生用孩童般稚趣的语言为少年儿童题词：“数学好玩”.对当下的中学生来说，数学真的好玩吗？高考的激烈竞争使数学成了“烈火上的舞者”，“数学无用”的论调在败坏着数学的美.让数学有趣，学生喜闻乐见，是当今数学教育工作者的迫切追求.我们要用好“数学探究”、“数学建模”等新型的学习活动，创设耐人寻味的问题情境，一个好的问题足可以吸引学生深入探究，不断提出新的问题并解决，还乐此不疲.

要想开展高质量的“数学探究”活动，发人深思、有探究价值的素材至关重要.无论是教师精心选取，还是学生自主发现的，首先要能吸引学生目光.这道题目于教师来说，是“闲着没事儿干了”才会研究，但就被学生看上了.是它开放的题境唤起了学生的探究欲望，是学生探究的热情点燃了它.我们应该以一颗敬畏的心对待这份热情，努力让数学活动更有趣，不断激发学生的学习热情，让探究之火烧得更旺.

爱因斯坦说过：“提出一个问题往往比解决一个问题更重要，因为解决问题也许仅仅是一个教学上或实验上的技能而已，而提出新的问题往往需要有创造性的想象力.”提出问题需要学生用数学家的眼光看待生活现象，从数学的角度发现和提出可探究的新问题.学生在解决问题后的对问题不断地追问，便是一种“数学家的思考”.基于兴趣的目光，着实难能可贵，我们应该予以赞赏；意想不到的问题，是宝贵的探究资源，我们当倾心指导，着眼于创新思维能力的培养，让他们拥有数学的眼光.

3.2 引导学生掌握探究的方法，让数学有迹可循

教学改革从未停歇.教学主张经历着“授之以鱼、授之以渔、授之以欲”的变革过程，为着人的更好的发展.而好的数学探究往往要经历“欲、鱼、渔”的过程.一个好的素材引发学生的探究之欲，为解决问题需要积累基础知识，还要掌握应用知识解决问题的方法.热情驱使下的探究，不需要教师过多的讲授.教师当做学生的指路人，于学生疑惑处指点迷津，帮助学生理出一条可行的探索之路.怎样确定最小的圆形包装纸，犹如无底洞不可捉摸，教师引导学生采取比较策略，在已有工作的基础上寻找更小，比直接探寻最小更加清晰易操作.在从特殊到一般的探究过程中，问题也变得越来越明晰简单.一旦学生拥有了“欲、鱼、渔”，学习便可以随时随地发生，协作交流也可以随时随地进行，成长就会自然而然.

研究性学习难以有效开展的原因多是难度大，见效慢.不像一个单纯的数学问题，题境封闭，方向明确，答案固定.一个可研究的问题往往是开放的，学生做探究难以深入下去的重要原因是摸不着头脑，搞不清方向.怎样用一张圆形包装纸包住正四面体？不易操作，也难想象，于是空间问题“平面化”，而展开图也是多样式的，从哪包起？再回到空间，考虑到正四面体和圆都是“对称”的，只需要探讨一种展开图，圆心在一个底面内移动即可.这是抽象，是建模，是培养学生数学建模素养的绝佳体验.

数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的过程.数学建模要求学生能“用数学的语言表达世界”.而“世界”是纷繁芜杂的，这就需要学生的综合分析能力、创新创造能力.从提供的答案看，命题者对该问题的建模过于理想化了.追求最优化一直是数学应用的重要方向.正是对最优的执着追寻，才有了前面的探究.在“现实问题”面前，学生心中是一团乱麻，教师要帮助学生条分缕析，从乱中理出序来，让数学有迹可循.

3.3 促成学生思考力的提升，让数学有深度

《普通高中数学课程标准（实验）》指出，高中数学课程应提倡实现信息技术与课程内容的有机整合.鼓励学生运用计算机、计算器等进行探索和发现.信息技术的广泛应用正在对数学课程内容，数学教与学的方式等产生深刻的影响.借助数学软件工具，学生可以体会到数学的深度、领略到数学的无限魅力.

数学是思维的体操.有时候，体操的难度系数偏大些，学生的思维有到达不了的彼岸，便可以通过技术来搭桥，帮助学生把抽象变得直观，给思考一个方向，使之得以继续，把体操做得更优美些.本题中的圆包正四面体靠手工操作太难，误差很大，仅凭大脑解决又需要相当高的空间想象能力，而借助《几何画板》就可以清晰地展示，何乐而不为？当得到半径r′与a的关系，求这么复杂的分式函数的最值完全没必要，借助《几何画板》的绘图功能使结果一目了然，可以解放大脑来分析结果.技术的助力，不仅能弥补思维之不足，还能为思维插上翅膀，使之越过障碍，往更广阔的领域翱翔.

数学思维是隐形的技术.信息技术于数学只是一种辅助工具.信息技术的使用应恰到好处，防止代替大脑思考.对两个角露出来的情况，当O′与O非常靠近时，角C究竟能不能被完全覆盖，就连《几何画板》作图也会因为线条的粗度给人能覆盖上的感觉.这就需要大脑来判断，只要点A在圆外，AC外的弓形就盖不上点C.当O′，B′都动起来时，《几何画板》也“无能为力”了，需要严谨的代数求证.技术，使用而不依赖，借以锤炼思维的深度，使思维更流畅.提升思考力，才是正道.