基于CFD方法的某化学品船型优化及船舶阻力性能数值预报

殷晓俊, 任海奎(上海船舶运输科学研究所 航运技术与安全国家重点实验室,上海 200135)

基于CFD方法的某化学品船型优化及船舶阻力性能数值预报

殷晓俊, 任海奎
(上海船舶运输科学研究所 航运技术与安全国家重点实验室,上海 200135)

对快速性技术指标较好的某化学品船进行线型优化研究。利用GMS前处理软件对船体线型进行若干变化，利用势流兴波软件RAPID进行快速计算，得到船体周围兴波及船体表面压力分布情况，从而选择较优方案。利用商业软件STAR-CCM对原型和改型的阻力性能进行黏性流体数值计算，定量分析改型后船舶阻力的减小量，为模型试验提供参考依据。模型试验结果表明,改型船的阻力较原型进一步降低，与计算流体动力学(Computational Fluid Dynamics,CFD)计算结果吻合良好，新匹配的螺旋桨推进性能较原型明显提高。

船型优化；计算流体力学；模型试验

0 引 言

船体线型优化是船舶阻力理论应用和其他研究工作中最重要的环节之一，在船舶主尺度、排水量和设计航速给定的条件下设计出阻力更低和推进效率更高的船型，是造船工作者的主要研究目标。随着国际船级社协会(International Association of Classification Societies,IACS)出台新造船标准，绿色船舶以其节能、环保的特性而受到业界关注，对现代船型优化及新船型开发越发重视。早期主要通过系列模型试验获取较优船型，通过比较若干个方案选出阻力性能最好的船型，这种方法不仅会耗费大量的劳力和时间，而且有一定的局限性。近年来，随着计算流体动力学(Computational Fluid Dynamics,CFD)理论不断进步和计算机技术的发展，基于CFD理论的船型优化设计已成为热点。

用于船舶阻力预报及船型优化的CFD方法主要有，基于势流的兴波阻力数值预报优化方法和基于黏性流场雷诺平均方程(Reynolds Averaged Navier-Stokes,RANS)求解的优化方法。目前已有不少应用势流兴波方法进行船体线型优化的案例，国内部分科研院所及船厂已在船舶势流兴波数值方法的研究与应用上取得显著进展。随着黏性流体理论及计算机技术不断发展，考虑自由液面的黏流求解已逐渐应用到船舶研究与设计中，黏流数值方法不仅可用于船体阻力、自由面及伴流计算，而且可考虑船、桨、舵及附体之间的相互干扰。近年来，国内通过对商业软件进行开发应用，在黏流CFD计算水动力学问题方面也已取得很好的成效[1]。

1 势流兴波数值方法

船舶以常速U沿x轴正向运动，O-xyz为固定在船上的直角坐标系，xy平面与静水面重合，z轴垂直向上。在O-xyz坐标系中流动的为定常势流，忽略表面张力的影响，水域为无限水深、不可压缩流体。

根据以上假定，船舶绕流流场存在速度势，且满足以下方程和边界条件。

1)在流场中满足Laplace方程，即

φ=0

(1)

2)在自由面上满足运动学边界条件和动力学边界条件，即

φxζx+φyζy-φz=0,z=ζ(x,y)

(2)

(3)

3)在船体表面满足不可穿透条件，即

φn=0

(4)

4)在无穷远前方满足辐射条件，即

φ=-Ux

(5)

求解船舶兴波问题就是求解上述方程组，难点之一在于自由面边界条件的非线性。自由面边界条件(即式(2))是非线性方程，且自由面初始位置不可知。求解该非线性方程的方法通常是在一个已知的基本解的基础上对自由面边界条件进行线性化处理，然后采用迭代的方式求解。假定此次迭代的结果是对上次迭代的小扰动，进一步对该扰动作线性化处理，并在上一次迭代得到的自由面上满足边界条件。

2 黏流CFD方法

2.1 控制方程

基本控制方程包括连续方程和动量方程。

1)黏性可压缩流体的连续方程(质量守恒方程)为

(6)

2)动量方程为

(7)

式(6)和式(7)中：ρ为流体密度；p为静压力；τij为剪切应力；ρfi为i方向重力体积力。

2.2 湍流模型

湍流方程使用两方程的Realizablek-ε模型，不可压缩流体的k和ε的输运方程为

(8)

(9)

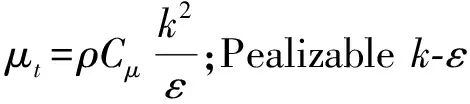
Realizablek-ε模型有明显的优势，可保持雷诺应力与真实湍流一致，能更精确地模拟平面与圆形射流的扩散速度，同时在计算旋转流、带方向压强梯度的边界层及分离流等问题中，所得结果与真实情况较为符合。

2.3 区域网格划分及相关参数设置

由于船舶左右舷是对称的，因此计算时只取船体的一半进行建模和计算。坐标原点位于船舶水线面、中纵剖面和艉柱(0站)的交点处。计算域外边界，上游沿船首方向延伸1倍船长，下游向船尾方向延伸2倍船长，船侧取1倍船长，底部取2倍船长。z=0以下为水，z=0以上为空气。分别对船体艏部、艉部、船体周围、自由液面附近及船体兴波进行局部加密处理，加密后网格总量约为200万个,图1为STAR-CCM计算船舶阻力计算域外边界网格情况，图2为船体周围局部网格划分情况。图1中,流域右侧为速度入口，左侧为压力出口，底部和顶部为可滑移壁面条件，两侧为对称边界条件，船体设为壁面。湍流模型选择Realizablek-ε模型。原型和改型在数值计算过程中采用完全相同的网格划分策略、物理模型及相关计算参数设置。

图1 计算域外边界网格划分情况

图2 船体周围局部网格划分情况

3 船型基本参数及线型优化

研究对象为某快速性指标已较好的化学品船(原型)，表1为该船的基本参数。此次船型优化的限制条件是保持原型的主尺度和排水量不变。该船的设计航速对应的傅汝德数Fr为0.168，兴波阻力仍占据一定比例。因此,通过降低船舶兴波来降低剩余阻力进而减小其总阻力是提高船舶快速性能的主要途径[2]。

长宽比超过6.0，船宽吃水比约为2.8，在肥大型船内比较适中，有利于进行船型优化，提高其快速性能。

3.1 艏部优化

艏部在原型的基础上设计一个体积较大的SV球艏，浸没在设计吃水以下，横剖面呈梨形，原型与改型球艏特征见表2。若球艏大小与位置设计恰当，球艏在航行中产生波浪的波谷和艏波的波峰处于相同位置，使合成波高较原来的艏波高有所减小，则球艏的兴波对主船体的艏横波形成有利干扰，使船舶兴波阻力得以减小，阻力得以降低。

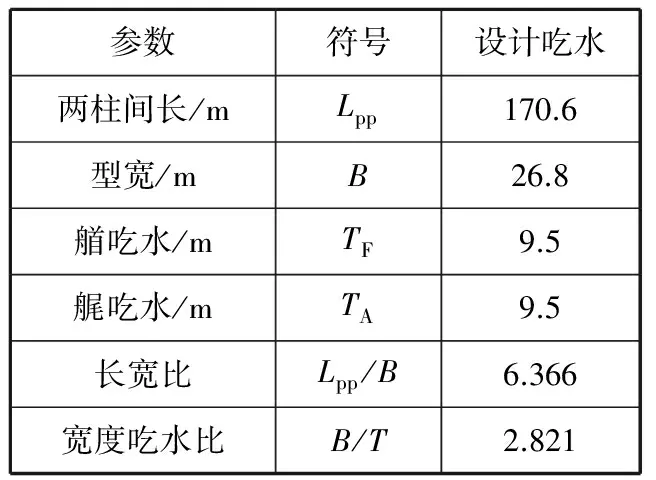
表1 船舶主尺度

表2 原型与改型球艏特征 %

针对船艏线型，除了球艏的优化外，还对平行中体与19站之间的线型进行优化。一方面减小设计吃水附近的水线进流角并削瘦肩部，从而减小产生的肩波;另一方面减小各站舭部附近的宽度，改善低压区域，同时优化艏部横剖面面积，使船体表面压力分布变得均匀，降低黏压阻力[3]。

3.2 艉部优化

该船原有主机额定功率MCR为6 480 kW×136 r/min，现在优化线型采用新的MCR为5 180 kW×173 r/min,并带有减速齿轮箱，减速比为1.957∶1，相当于在采用低转速主机的同时又不增加主机尺度,因为低转速主机需要更大的机舱布置空间，也不便于艉部线型的优化。

对于最佳效率线设计的螺旋桨，敞水效率ηo为

ηo=-αEln Bp+βE

(10)

直径系数δ为

Ln δ=αDln Bp+βD

(11)

直径D为

(12)

螺距p为

(13)

由式(10)和 (11)对螺旋桨要素进行全微分可得

(14)

由式(14)可知，在确定主机功率和航速的情况下提高螺旋桨效率ηo,减小转速n或增大VA。增大VA即减小伴流,但伴流的减小同时还会减小船身效率ηH,因此伴流的减小对推进效率ηd的变化具有不确定性，在螺旋桨型式已定的情况下，只有通过减小转速n(即增加桨径)来达到[4]。

原主机对应的桨径吃水比偏小，即还有较多吃水余量可利用。因此,在船型优化过程中优选主机类型，通过减速齿轮箱减速使新设计桨直径增大，有利于推进效率的增加。

改型方案的设计桨采用大直径SKEW型4叶螺旋桨，并对螺旋桨进行叶梢卸载设计，即改小叶稍处的螺距以确保螺旋桨不会因直径的增大而产生额外的激振力。针对艉部线型 , 先提升轴高以符合大直径螺旋桨叶稍与船基线处的安全距离，再抬升0站处的船中纵剖线，以加大桨叶与船体的间隙比，避免船体产生较大振动。在确保船舶机电设备布置的情况下调整1～4站接近舭部处的宽度，使球艉特征更加明显。这样可使伴流分布均匀，并有利于改善艉部振动。另外，接近船尾处的纵剖线上抬平缓，既可弥补排水量，也有利于使螺旋桨来流均匀[3]。

4 计算结果及分析

数值计算内容包括利用势流兴波软件RAPID对原型和改型进行数值计算，分析船体周围兴波、船体表面压力分布及半宽处纵切波分布情况;然后利用商业软件STAR-CCM分别对原型和改型的阻力性能进行黏性流体数值计算，定量分析改型后船舶阻力的减小量。原型和改型均分别进行相应的模型试验。

4.1 势流兴波计算结果分析

利用势流软件RAPID对原型和改型设计吃水(Fr=0.168)处的兴波进行数值计算，计算结果见图3。

由图3可知:原型方案的艏横波与艏肩波两处波系较为明显，而改型方案的艏横波与艏肩波叠加后使船体两侧的波系明显减小，这得益于球艏优化后有益干扰的增加和艏部进流角的改善；船体艉横波、散波、艉肩波及舭部区域压力梯度相比原型都有所下降，说明艉部线型优化效果明显。图4为原型和改型在半宽处纵切波面高度分布图，横坐标为半宽处纵向不同位置，纵坐标为波面高度。由图4可知，改型方案艏部的首个切面波峰有所下降，同时平行中体到艉部的切面处，波峰波谷之间的摆幅也明显下降。

图3 原型与改型波形与压力分布图(Fr=0.168)

图4 半宽处纵切波分布图

4.2 黏流计算结果分析

利用商业软件STAR-CCM对原型和改型设计吃水(Fr=0.168)处的船模阻力进行数值计算，计算结果见表3。

表3 原型与改型船模阻力数值计算与模型试验结果

由表3可知:数值计算能很好地模拟船模阻力试验，与试验结果较为符合，特别是船模总阻力，偏差<1%；对比原型与改型的试验结果也可看出，改型的阻力性能较原型得到较大提高。

图5和图6为通过黏流数值计算得到的原型和改型(Fr=0.168)的波形图，与图3中通过势流方法得到的原型和改型兴波图相似，说明了2种方法的可靠性。

图5 原型波形图

图6 改型波形图

为分析优化线型后船尾伴流的变化，分别截取原型和改型艉部与舵之间相同位置截面上的伴流场(见图7和图8)。从图7和图8中可看出，改型艉部伴流较原型整体减小，伴流梯度更加均匀，有利于减小艉部振动。

图7 原型船艉伴流等值线图

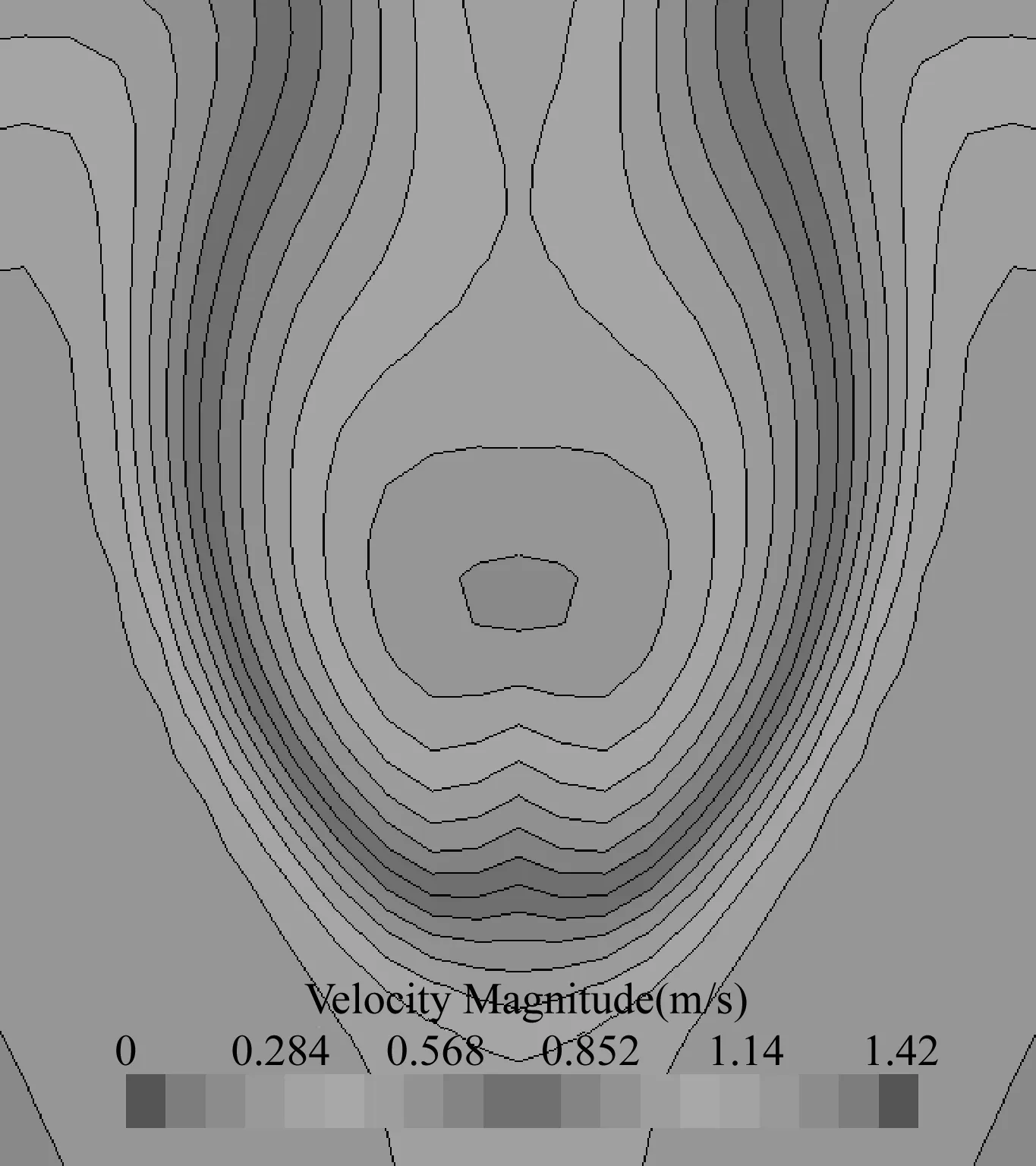
图8 改型船艉伴流等值线图

4.3 模型试验结果

船舶航速-有效功率图及阻力自航试验结果对比见图9和表4。试验结果表明，改型船的剩余阻力系数在设计吃水的设计航速(Fr=0.168)下降低约15%，对应的有效功率可下降3.6%～4.8%。螺旋桨的推进效率因艉部改型与增加桨径的因素而提高超过11%。值得注意的是，增加齿轮箱会降低轴系效率，但对比螺旋桨推进效率的提高则是小量，最终该船的快速性指标在同类船型中已达到一流水平[5]。

图9 航速-有效功率图

航速/kn设计吃水(改型/原型)/%PeQPC12．0-4．8110．8512．5-4．6011．2913．0-4．1211．5613．5-3．7311．5214．0-3．5911．2614．5-3．5911．05

5 结 语

通过CFD计算软件对原型和改型船的快速性能进行定性与定量化计算，同时对船舶主机进行优选，分别对原型和改型船进行模型试验对比分析及研究，可得到以下结论。

1)设计适当的船体球艏与设计吃水处的进流角，可有效降低船舶的整体阻力。

2)小型主机增加减速齿轮箱并调整艉部线型以满足桨叶的空间布置后，可设计大直径螺旋桨以获得更好的推进效率，同时避免低转速大型主机对艉部线型优化的限制。

3)CFD软件可定量计算船舶阻力等参数并准确评估船体伴流场，与模型试验结果吻合度良好，其阻力计算已达到一定精度，可更好地为模型试验与航速预报服务。

[1] 陈伟民, 陈霞萍. 计算流体力学在船舶线型优化中的应用[J]. 上海船舶运输科学研究所学报,2001,30(1):30-32.

[2] 高玉玲,陈霞萍,柳卫乐,等. 超大型液化石油气船线型优化设计与试验研究[C]//2013年船舶水动力学学术会议论文集.北京:中国造船工程协会,2013:158-162.

[3] 盛振邦，刘应中．船舶原理[M]．上海：上海交通出版社，2003．

[4] 薛安国. 大直径低转速螺旋桨的收益及其应用[J]. 船舶工程, 1984(2)：15-19.

[5] 闫磊, 卢华，陈霞萍. 某大型散货船船型优化设计与试验研究[C]. 南京:船舶水动力力学学术会议,2015.

Hull Form Optimization of a Chemical Tanker and Numerical Prediction of the Resistance Performance with CFD Method

YINXiaojun,RENHaikui
(State Key Laboratory of Navigation and Safety Technology, Shanghai Ship & Shipping Research Institute, Shanghai 200135, China)

The hull form optimization of a chemical tanker in terms of good speed and resistance performance is presented. The optimal scheme is decided according to the surface pressure distribution around the hull obtained from the calculation with the potential flow wave making software RAPID. Numerical calculations of the viscous fluid resistance performance of the original and the optimized are performed by means of the commercial software STAR-CCM. The calculated resistance reduction is used as the reference basis of model tests. The model test data proved the success of the optimization and the reliability of CFD(Computational Fluid Dynamics) calculation. The propulsion performance of the new matching propeller is significantly improved.

hull form optimization； CFD； model test

2016-09-28

殷晓俊(1982—)，男，上海人，助理研究员，主要从事船舶水动力性能研究。

1674-5949(2016)04-0008-06

U661.31

A