波流作用下柔性立管载荷响应数值分析

吴梓鑫， 陈昆鹏(上海船舶运输科学研究所 航运技术与安全国家重点实验室， 上海 200135)

波流作用下柔性立管载荷响应数值分析

吴梓鑫， 陈昆鹏
(上海船舶运输科学研究所 航运技术与安全国家重点实验室， 上海 200135)

结合商用软件Fluent 14.5自定义函数(UDF)功能，采用速度边界造波法和阻尼消波技术，通过流体体积函数(Volume of Fluid, VOF)追踪自由液面，建立波浪、波流数值水池。采用双向耦合分离法思想，借助Workbench 14.5流固耦合模块System Coupling将流域和结构域计算数据交互传递，在数值波浪、波流水池中对长径比为8的柔性立管进行双向流固耦合模拟，分析其载荷响应，得出波浪场中不同流速下受力点的变化情况及不同波流方向下振动平衡状态的变化情况。

数值水池； 流固耦合； 柔性立管； 载荷响应

0 引 言

目前国内外众多科技工作者已在波浪与结构物相互作用的试验研究和数值分析上取得许多成果，诸多结论已投入工程应用。例如：TAYLOR等[1]在小流速假定下用零流速时的三维脉动源加上流速修正项代替移动脉动源，利用绕射理论模拟三维浮体与波流的相互作用；周正全等[2]给出波流联合作用下绕射问题的时域解理论模型，证明利用入射波势和辅助辐射势计算三维结构物波浪绕射力的可行性；SARPKAYA等[3-4]分析圆柱体阻力系数在波流场中的变化；HAN等[5]运用Hamiliton原理和Kirchhoff假设研究上端自由而下端支撑在海底条件下立管在波流作用下的轴向与横向振动特性。

在数值研究方面：ATADAN[6]考虑基于非线性弹性理论的剪切效应，通过理论求解和数值模拟的方法确定海洋立管在波流作用下的动力响应；SHAH等[7]将海洋立管下端支撑而上端设置为简支，研究其在波流联合作用下的共振问题，并分析了流引起的主共振和波流联合作用引起的组合共振特性；李军强等[8]基于ANSYS和ABAQUS/Aqua等有限元分析软件对波流联合作用下深水立管的非线性动力响应进行诸多研究。

随着商用软件功能日趋完善，数值仿真已成为研究海洋问题的新方法，这里借助软件Workbench 14.5模拟立管在数值水池中的运动响应，并进行相关分析。

1 数学模型

1.1 流体控制方程

假设流体为不可压缩黏性流体，依据流体力学理论，其运动控制方程如下。

(1) 连续性方程为

(1)

式(1)中:ρ为流体密度;v为流场速度矢量。由于流体不可压缩，连续性方程简化为

(2)

(2) 对于黏性流体运动，当黏度为常数时，有动量守恒(Navier-Stokes，N-S)方程

(3)

ρ为常数时，流体不可压缩，N-S方程简化为

▽2v

(4)

1.2 结构控制方程

假定结构为线弹性，相对于其平衡位置作刚体运动和变形。结构经有限元离散后的动力学方程为

(5)

1.3 边界条件

数值模拟中，流体计算主要需满足自由液面条件和壁面条件。对柔性立管的计算还需满足流固耦合界面条件。

1.3.1 自由液面条件

数值水池中流体上方为空气，在自由液面处必须同时满足运动学条件和动力学条件。对于运动学条件，针对不同的液面追踪方法，有不同的数学表达方式;对于动力学条件，则须满足表面应力条件。假设不计自由表面张力，表面应力条件可表示为

(6)

(7)

式(6)和式(7)中：un为垂直于自由表面的法向速度(流域中外法向为正)；ut为切向速度；p0为表面大气压强。

1.3.2 壁面条件

这里数值模拟中采用不可滑移壁面条件

v=vb

(8)

式(8)中：vb为相对于连体坐标系的运动速度。

1.3.3 流固耦合界面条件

流固耦合界面上边界条件包括运动学条件和动力学条件。

(1) 运动学条件：流固交界面上法相速度保持连续。

vfn=vf·nf=vs·nf=-vs·ns=vsn

(9)

式(9)中：nf为流体边界外法线向量；ns为固体边界外法线向量。

(2) 动力学条件：流固交界面上法向应力保持连续。

σijnsj=τijnfj=-τijnsj

(10)

式(10)中：τij为流体应力张量的分量。

2 柔性立管在波流作用下载荷与响应分析

数值模拟借用软件平台Workbench 14.5，流体域通过Fluent计算，结构域选用Transient Structural计算，数据传递通过System Coupling模块实现，后处理由CFD-Post完成。

2.1 模型建立及参数设置

2.1.1 流体域建模与设置

所模拟的余弦波波高为1 m，水池水深为5 m，周期为3.737 s，具体参数见表1。数值水池工作区60 m，消波区20 m，水深5 m，水面以上3 m为空气，立管直径1 m，距水池前段30 m，距左右边界均为5 m。水池模型示意见图1。

表1 余弦波参数

图1 数值水池模型示意

采用结构网格划分模型，在波长方向单个网格尺寸为1%波长，自由液面上下1个波高内网格高度为5%波幅，远离自由液面处网格渐稀。以立管为中心，在xy平面立管周围10 m×10 m内网格加密。

左端入口为速度入口，右边界设置为压力出口，上边界设置为压力入口，底边界、水池两壁面及立管边界为无滑移固壁条件。造波、消波、压力出口及自由液面捕捉通过Fluent软件自定义函数(UDF)自编程序实现。

采用Fluent中三维非定常分离隐式求解器求解，湍流模型选用RNGk-ε，压力方程选用加权体积力格式，压力速度耦合方式采用PISO算法，体积分数方法为几何重构，动网格更新方法选用扩散光顺。流体域中与立管接触面设置为流固耦合面。时间步长为0.005 s。

2.1.2 结构域建模与设置

立管直径为1 m，壁厚为0.05 m，密度为7 850 kg/m3，具体参数见表2。立管与流域接触面为流固耦合面，根据文献[9]将底端设置为简支，顶端限制其水平位移。此外，考虑到文献[10]中涉及涡激振动和对预紧力进行计算分析，设置立管顶部预紧力为20 000 N。时间步长为0.005 s。立管表面网格与其接触流体面网格并不需要完全对应，经过试算，单位网格尺寸设置为0.1 m。

2.1.3 流固耦合模块设置

流体域和固体域分别设置完成后，通过System Coupling模块将两者同步连接，定义上述2部分流固耦合面为数据传输面，设定计算顺序为先计算流体域再计算固体域，设置时间步长为0.005 s，计算时间为30 s。

2.2 数值模拟结果分析

为研究不同方向波流联合作用下柔性立管的载荷响应，模拟表3中的工况。

表2 立管模型参数

表3 波流速度

为兼顾准确性和工程需要，采用文献[11]中提出的波流水平速度叠加法进行波流联合作用的数值模拟，以探求波浪参数在海流存在条件下的变化情况，其速度关系为

uwc(x,z,t)=uw(x,z,t)+uc

(11)

式(11)中：uwc(x,z,t)为波流联合场水平速度；uw(x,z,t)为波浪场水平速度；uc为均匀流场水平速度。

2.2.1 立管受力分析

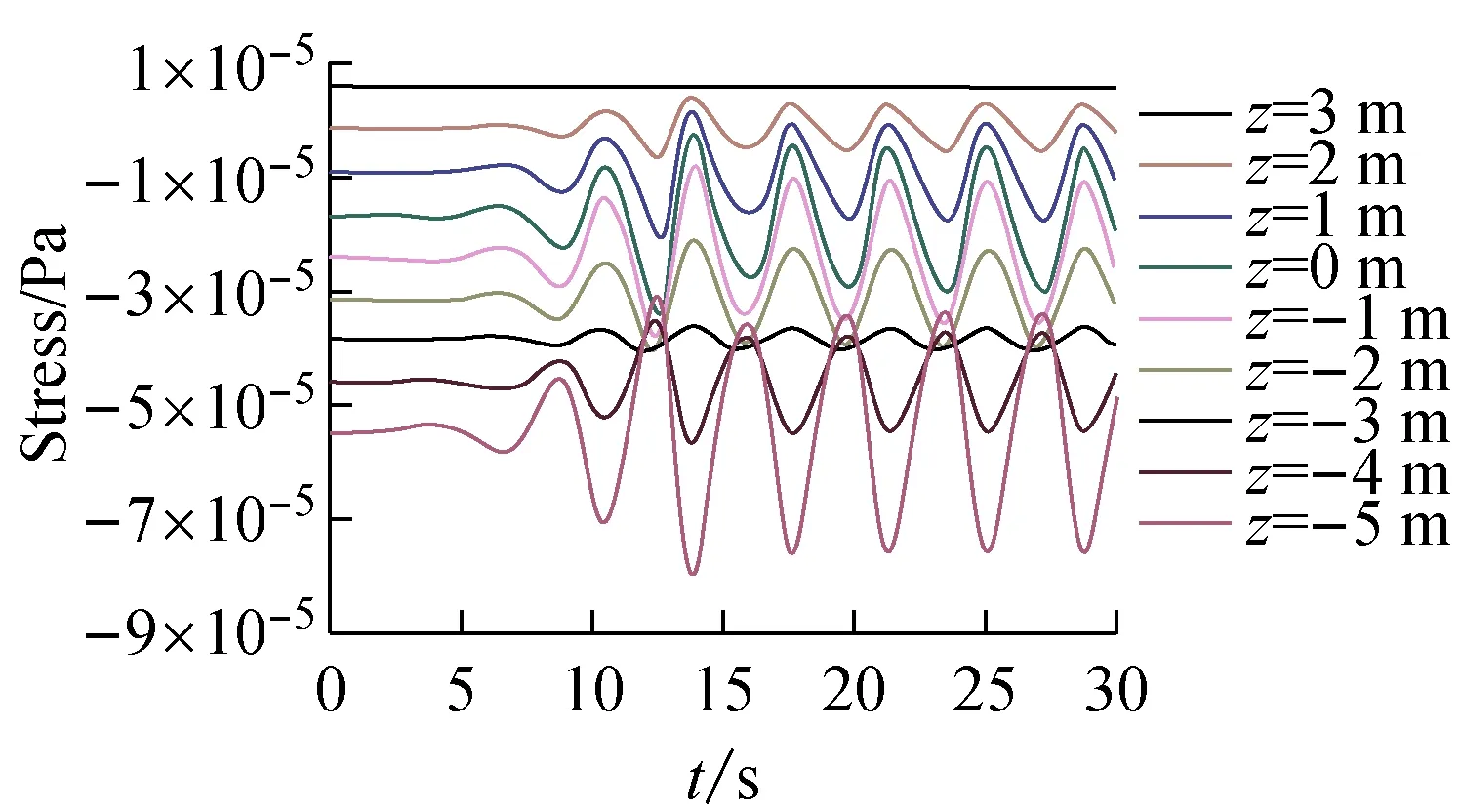
数值水池中波浪自左向右传播，在立管迎浪面最前端z=3 m至z=-5 m每隔1 m设置1个点，共设置9个点监测其应力，压力<0，拉力>0，立管在各水平高度下的压力变化时程曲线见图2。

a) Case 1

b) Case 2

c) Case 3

d) Case 4

在单独波浪场中，立管最大受力位于立管底端，整体沿水平高度向上递减，立管顶部承受拉力，各点受力周期相同。在波流联合作用下，波流同向时Case 2中立管受力曲线分布与单独波浪场中相似，最大受力位于立管底端，但在流的作用下立管受力上移。Case 3中立管受力分布发生显著变化，立管受力向中间段趋近并以该水平高度向两端逐渐减小，底端处由持续受压状态转为压力和拉力交替循环。当波流相向时，Case 4中立管的受力状态与Case 2相近。

柔性立管在数值水池中的水平作用力系数时程曲线见图3。波流同向时，在同一周期中由于流的作用，水平作用力系数较单独波浪中正向幅值增大、负向幅值减小，且由于拖曳力正比于流速平方，Case 4中当流速增加时幅值增减变化更为明显,当波流相向时水平作用力系数正向幅值正值比单独波浪场中小，负向幅值比单独波浪场大。

2.2.2 迎浪向振动分析

监测点在迎浪向的振动时程曲线见图4，随着波浪的传递作用，在约5 s时立管开始有较为明显的振动，振动周期与波浪周期相近。波流同向时，由于流的作用加上立管两端的约束和静水压力影响，在波浪传至立管处前时监测点在迎浪向已有一定的位移，且在立管中间部分(即水深z=-1 m和z=-2 m区间内)位移最大，当波浪传至立管处时监测点开始出现周期性振动，周期仍与立管单独波浪中的振动周期基本相同。

图3 柔性立管水平作用力系数曲线

Case 2中运动趋势与单独波浪中相似；Case 3中监测点振动曲线呈现出明显的“峰尖谷坦”特性。波流相向时，由于反方向流的作用加上立管两端约束条件的限制，立管迎浪面的初始位移有正有负，约为压缩的“s”形。在波流联合作用下，向迎浪向运动时速度较慢，向流向运动时速度较快，运动周期同样为3.73 s。

各算例中柔性立管监测点在迎浪向的振幅汇总见图5。虽然加载流的大小和方向存在差异，但振幅并没有显著的区别。稳定状态时立管在z=0 m和z=-1 m处振幅最大，向上/下两端逐渐减小，最大振幅区域均位于自由液面以下2 m内。

以流速和波速的比值作为横坐标，选取算例中最大迎浪向振幅值(即各算例中z=-1 m处的振幅值)作为纵坐标，绘制成最大振幅趋势曲线(见图6)。由此可推断出，在该模拟范围内，当波流相向时，随着流速减小，立管迎浪向振幅减小；当波流同向时，随着流速增大，立管振幅增大，当流速与波速的比值约为25%时，振幅达到最大，此后流速继续增大，立管振幅减小。

a) Case 1

b) Case 2

c) Case 3

d) Case 4

图5 监测点迎浪向振幅汇总

图6 立管迎浪向最大振幅随波流比值走势

立管在数值水池中振动时其平衡位置相对于静止位置发生偏移，各算例立管在迎浪向振动的平衡位置偏移原静止位置(见图7)。在单独波浪场中，立管振动平衡位置较静止位置在迎浪向有一定的位移，最大振动平衡位置区域位于自由液面以下约4 m处。加载流之后，波流同向时，最大平衡位置上移至自由液面以下1～2 m区域内，当流速为波速的20%时最大偏移值约为单独波浪场最大偏移值的8倍，流速加大到40%波速时最大偏移值约为单独波浪场中23倍；波流相向时，各水平位置的振动平衡位置的变化与波流同向时差异较大。由于流的作用对立管振动平衡位置的影响非常显著，因此在波流相向时，立管背浪面自由液面以下在流等外载荷作用下其振动平衡位置向迎浪向负方向偏移；而立管结构具有各向同性的属性使得迎浪面自由液面以下其平衡位置向迎浪向偏移，立管顶端水平位移受限，因此其自由液面以上部分振动平衡位置在原静止位置左侧，Case 4中立管迎浪面和背浪面立管振动平衡位置见图8。

图7 立管迎浪向振动平衡位置

图8 Case 4立管振动平衡位置

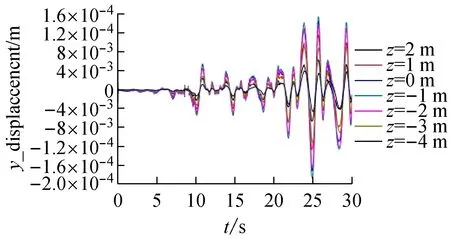
2.2.3 横浪向振动分析

数值水池中立管监测点在横浪向的振动时程曲线见图9。相比立管迎浪向振动，横浪向振动随机性更强，振动周期差异较大，但振幅最大区域依然位于自由液面以下2 m区域内。分析数据可得，当只有波浪作用时，横浪向振幅不到迎浪向振幅的0.1%。当波流共同作用时，横浪向振动不可忽略，波流同向中流速为波速20%时横浪向振幅为迎浪向振幅的17.18%，当流速增至波速的40%时横浪向振幅为迎浪向振幅的24.2%；而波流相向时，横浪向振幅为迎浪向振幅的1.11%。

a) Case 1

b) Case 2

c) Case 3

d) Case 4

2.2.4 轴向振动分析

监测点在立管轴向的振动时程曲线见图10。与水平面内振动不同，由于监测点在水平面内具有运动位移，而立管底端简支约束，上端只能进行轴向运动，因此各点在轴向的运动方向不再统一，当靠近底端部分位移>0时顶端位移<0，反之亦然。幅值方面，在立管顶部轴向运动幅值最大，而在自由液面以下2 m区域内轴向运动幅值最小。在单独波浪场和正负向流速为波速20%的波流数值水池中，各点轴向运动时程曲线约为余弦函数状，而当流速增至波速的40%时，时程曲线在单个周期内存在2个正向幅值和2个负向幅值，体现出流速较大时波流联合作用下立管运动的复杂性。此外，数据分析表明，立管轴向运动的周期与迎浪向的运动周期基本吻合。

a) Case 1

b) Case 2

c) Case 3

d) Case 4

图11 监测点轴向振幅

柔性立管在轴向运动振幅统计见图11。各算例中立管各水平位置在轴向的振幅变化趋势一致，均在立管中间位置，即迎浪向振幅最大位置z=-1 m处振幅最小，向上和向下振幅都逐渐增大。由于底端简支约束，振幅为0，且振幅由z=-1 m处向下为0的中间部分存在1个幅值转捩点，由图11可知该转捩点在z=-3 m附近。

3 结 语

基于黏流理论，以商业软件Fluent 14.5为平台，通过程序接口加载自编程序进行开发，采用速度边界条件造波法建立效果良好的波流数值水池。借助软件平台Workbench 14.5，通过流固耦合模块System Coupling连接流体模块Fluent和结构模块Transient Structural，数值模拟长径比为8的柔性立管在不同波流参数数值水池中的运动，从立管受力、迎浪向、横浪向和轴向振动等方面对柔性立管在波流联合作用下的载荷响应进行分析和研究。结果表明:在波浪场中，立管底端受力最大，沿轴向向上逐渐减小；当加载流速较小时，立管受力分布变化不大；当流速较大时，立管应力集中点上移。在模拟范围内，波流同向时，立管振动平衡位置向迎浪向偏移，迎浪向振幅随流速先增大，达到某一极值后减小；波流相向时，振幅大于单独波浪场中的振幅。此外，单独波浪场中，立管横浪向振幅很小，而在波流联合作用下横浪向振幅显著增大，不可忽略。

[1] TAYLOR E R, HU C S, NIELSEN F G. Mean Drift Forces on Slowly Advancing Vertical Cylinders in Long Waves[J]. Applied Ocean Research,1990,12(3):141-152.

[2] 周正全，张亮，戴遗山. 波流联合作用下的物体上的波浪绕射力[J]. 水动力学研究与进展 (A 辑)，1992，7(4)：476-483.

[3] SARPKAYA T, BAKMIS C, STORM M A. Hydrodynamic Forces from Combined Wave and Current Flow on Smooth and Rough Circular Cylinders at High Reynolds Number[C].Proceeding of 16thOTC, Houston,1984.

[4] SARPKAYA T, STORM M. In-Line Force on a Cylinder Translating in Oscillatory Flow[J]. Applied Ocean Research, 1985,7(4):188-196.

[5] HAN S M, BENAROYA H. Non-Linear Coupled Transverse and Axial Vibration of a Compliant Structure, Part 1: Formulation and Free Vibration[J]. Journal of Sound and Vibration, 2000, 237(5): 837-873.

[6] ATADAN A S, CALISAL S M, MODI V J, et al. Analytical and Numerical Analysis of the Dynamics of a Marine Riser Connected to a Floating Platform[J]. Ocean Engineering, 1997, 24(2): 111-131.

[7] SHAH K, FERZIGER J H. A Fluid Mechanician's View of Wind Engineering: Large Eddy Simulation of Flow Past a Cubic Obstacle[J].Wind Engineering, 1997, 67(4): 211-224.

[8] 李军强，刘宏昭，何钦象,等. 波浪力作用下海洋钻井隔水管随机振动研究[J]. 机械科学与技术，2004，23(1): 7-10.

[9] 罗冬冬. 剪切流下长径比对柔性立管涡激振动的影响[D].镇江：江苏科技大学，2014.

[10] 王成官. 海洋隔水管涡激振动特性的三维数值模拟研究[D].上海：上海交通大学，2011.

[11] 李玉成. 波浪与水流共同作用下的流速场[J]. 海洋工程，1983(4):12-23.

Test of Loads on Flexible Riser and its Response with Numerical Wave-Current Tank

WUZixin,CHENKunpeng
(State Key Laboratory of Navigation and Safety Technology, Shanghai Ship & Shipping Research Institute, Shanghai 200135,China)

Numerical wave/wave-current tanks with high effectiveness in wave-making and wave-absorbing functions are established on the platform of Fluent 14.5 with UDF programs by using velocity boundary and damping wave technique as well as VOF method. With the two-way coupling separation concept, transferring the data of the fluid domain and structure domain in the module System Coupling of the Workbench 14.5, the motion response of a flexible riser with the aspect ratio of 8 is simulated in the numerical tank, and the loads and response on the riser are analyzed.

numerical tank; Fluid-Structure Interaction; flexible riser; loads and response

2016-08-30

吴梓鑫(1989—)，男，江苏南通人，研究实习员，硕士，主要从事船舶水动力研究。

1674-5949(2016)04-0014-08

P756.2

A