基于KMV模型的公司债券信用风险研究

韦茜李立平董哲

（1.广西外国语学院国际经济与贸易学院；2.上海财经大学国际工商管理学院）

基于KMV模型的公司债券信用风险研究

韦茜1李立平2董哲2

（1.广西外国语学院国际经济与贸易学院；2.上海财经大学国际工商管理学院）

近几年债券信用风险有从中小公司向大公司蔓延趋势。本文采用KMV模型，选取大公司作为样本，分为低债券信用风险组、高债券信用风险组16家公司来研究债券信用风险问题。研究的时间跨度为2013、2014两年，选取无风险利率、总资产及增长率、股权价值及变化率、0.5的违约点等为参数，应用Matlab软件计算得出违约距离。结论显示，无论是从组别分析，还是从单个公司分析KMV模型均有良好的风险预测功能。鉴于风险频发，政策上应提前预测债券信用风险，打破对公司债券“刚性兑付”的传统。

公司债券 信用风险 KMV模型 违约距离

一、引言

作为企业直接融资方式的公司债券在我国发展时间较短，但发展较为迅速。2014年底，我国债券余额为34.9万亿元，其中公司信用类债券余额为11.42万亿元。随着中国证监会《公司债券发行与交易管理办法》在2015年1月的颁布，债券融资更加便利化，上市债券数量在短期内得到较快增长，2015年7月到12月间，公司债月均发行量超过1500亿元，全年发行量近1万亿元。另一方面，近几年债券信用风险事件有所增加，为此国家发展与改革委员会在2015年12月颁布了《关于简化企业债券申报程序，加强风险防范和改革监管方式的意见》，涉及防范债券风险的管理办法，对债券信用风险的防范势在必行。

债券的信用风险也一直是企业面临的重要风险控制问题。为有效控制信用风险，风险预测成了重要课题。准确度量信用风险，从监管层的角度来看有利于完善和发展多层次资本市场，保持经济活力，提高融资效率；从投资者角度来看有助于做出资产配置、分散风险的决策；对于上市公司来说，及时运用风险度量模型对公司的财务状况做出预测，对可能的债务危机提早预警，化解潜在信用风险；对研究者来说，运用合理的预测模型，搭建并完善信用风险数据库对完善我国信用风险研究有重要意义。

二、文献综述与KMV模型框架

（一）文献综述KMV模型是美国KMV公司研发结构化风险管理工具，KMV公司于20世纪90年代基于4700家违约公司搭建了违约距离和预期违约概率之间的映射关系。在此基础上测算出违约点。KMV模型往往先于债务人预测到信用评级的恶化,由此KMV模型具有较好的前瞻性(Forward-looking)预测效果。陈晓红、张泽京、王傅强（2008），刘澄、张玲（2013）认为在众多风险测量模型中KMV模型更适合对我国公司的风险评估。

KMV模型最早在2000年被引入我国，张玲、张佳琳（2000）尝试将原始KMV模型直接运用于我国的股票市场。现在对KMV模型的研究集中在两个领域，其一是KMV模型改进修正结合应用研究，其二更多的是单纯的KMV模型应用研究。前一种研究来看，薛锋、董颖颖、石雨欣（2005）针对我国非流通股不上市，信用制度不健全的实际情况对KMV模型进行修正。史小坤、陈昕（2010）在对商业银行风险管理的研究中对KMV模型的违约点进行了修正。马若微、张微、白宇坤（2014）对上市公司违约研究中也对违约点进行了修正。周海赟、王晓芳（2015）针对信息不完善的现实情况在KMV模型中引入了灰色区域理论。在应用研究领域聚焦公司信用风险领域，闫海峰、华雯君（2009）对上市公司的信用风险进行ST与非ST分类研究，得出两者信用风险有显著差异。曾诗鸿、许程（2014）对7个战略性新兴产业14家非ST上市公司研究，得出这类公司发展稳定信用良好。陈晓红、张泽京、王傅强（2008）对中小上市公司的信用风险进行研究，也对资产规模与违约风险之间的关系进行了研究。与之类似王建稳、梁彦军（2008）也对上市公司规模与信用风险之间进行了研究。两者得出公司或者资产规模与信用风险或者违约风险负相关，由此大公司信用风险会偏低，近几年的情况是大公司违约事件也时有发生。因此本文重点以信用风险高的大公司为研究对象，为了使研究对象具有广泛性和说服力，研究对象既包括ST类也包括非ST类,在研究中对模型也做了相关修正，使模型更符合实际。

（二）KMV模型框架KMV模型的思想来Black-Scholes -Merton期权定价理论。从股东的角度，把企业的股权价值视为一个看涨期权；从债权人的角度，企业的股权价值视为一个看跌期权。在债务到期日，如果公司总价值大于公司的债务，违约风险高；如果债务到期日公司总价值小于公司债务，则该公司有足够的资产偿还债务，违约风险低。根据Black-Scholes-Merton期权模型的看涨期权与看跌期权的定价公式：

C代表看涨期权价格，K代表期权的执行价格，r代表无风险利率，σ是股票价格波动率，T是期权的期限。

依前面假定把借款企业的股权看作是看涨期权，运用Black-Scholes-Merton的模型推导出企业的股权价值E如下：

其中，E代表企业的股权价值，VA代表到期日公司的资产价值，DPT代表违约临界点，r代表市场的无风险利率，T表示考察是否违约的到期期限，σA代表企业资产价值在T时期内资产对数收益率的波动率。

对于上市公司来说，E、DPT、r、T是已知或者可以计算的数据，但VA和σA是未知变量。根据伊藤引理可以推导出公司资产价值VA、资产价值波动率σA、企业股权价值VE、企业股权价值波动率σE这四者之间的关系式：

结合前面关于VA和σA的关系式建立联立方程，解出企业资产价值VA、企业资产价值波动率σA。最后计算在KMV模型中违约距离定义：

笔者曾经考虑采用P=N（-DD）来度量违约概率，N（x）是标准正态分布的累计分布函数。但是考虑到我国的债券市场发展时间较短，并且一直以来有着“刚性兑付”的传统，真正违约的公司债券数量极少，很难建立起完整的违约距离和违约概率的对应数据库，因此并不以违约概率来衡量真实的信用风险。

三、实证结果与分析

（一）样本选取样本分为“高风险组”与“低风险组”，其中“高风险组”选取2014～2015年违约的公司债券，是为了便于利用2013年和2014年滚动数据进行动态监控。利用2013年的数据建模、对2014年的违约风险进行预测，并用2014年的数据建模，对2015年的违约风险进行预测。运用滚动数据预测、动态监控的优势在于：可以用前一年发生的债券信用危机来对本年的预测进行证实或者证伪。同时选取同期信用债券但评级经营状况良好、资信评级较高（均为AA+或AAA）的“低风险组”作为对照组。每组为8家公司的8只债券，共16只债券。如表1所示：

（二）参数设定

（1）无风险利率。在目前我国学术研究中无风险利率的参考指标，以中国债券信息网公布的1年期国债利率和央行公布的1年期银行存款基准利率最为常见。1年期国债利率由于二级市场的存在，每日都有一定程度的波动性，具有更强的时效性。因而本文分别选取2012～2013年度和2013～2014年度一年期国债收益率的平均值作为无风险利率指标。由此2013年度无风险利率为3.3021%，2014年度无风险利率为3.4983%。

表1 低信用风险和潜在违约的两组公司

（2）公司资产价值增长率。公司资产价值的增长是一长期过程，但我国的证券市场目前依然具有很强的投机性，在短时间内股价波动情况依然明显。选取债券发行人在2013年末和2014年末的总资产当期同比增长率作为公司资产价值增长率，来计算公司资产价值的期望值。

（3）企业股权价值。我国国有股份股权分置的格局依然存在。上市公司一部分股权在交易所流通，称为流通股；另一部分股权暂时不上市流通，大多为国有股或法人股。非流通股原始成本远低于流通股。在实证分析中，如果忽视了非流通股低廉的成本，得出的上市公司股权价值是不准确的。修正后的股权价值计算公式为：

E=流通股收盘价×流通股股本+每股净资产×非流通股股本（5）

在计算公司股权价值时采用上市公司季度平均成交价格（区间均价=［区间成交额(千元)×1000］／［区间成交量(手)×100］）乘以流通股股本得到流通股股权价值，用季报公布的每股净资产乘以限售股股本得到非流通股股权价值（见表2）。

表2 2013～2014年末两组上市公司股权价值（单位：亿元）

一般认为股票市场在一年的交易日为250天，股权价值波动率计算公式：

运用公式，可得到上市公司2013年、2014年股权价值年化波动率（见表3）。

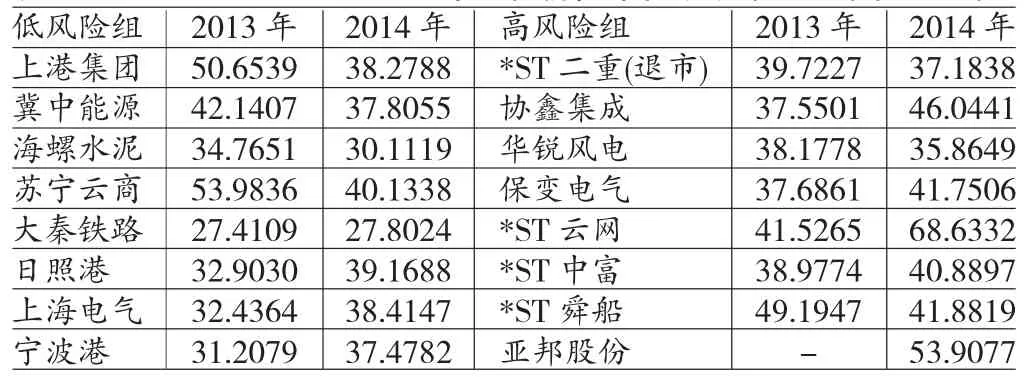
表3 两组公司2013～2014年股权价值年化波动率（单位：%）

（5）违约点。在KMV原始模型中，违约点是通过4700余家美国公司实证研究得到的经验数值，在这个临界值上，债券违约率最高。违约点一般等于公司短期负债加上0.5倍的长期负债。

我国公司债券起步晚，0.5这一系数是否适合中国国情，在学术界还未得出一致的结论，笔者暂时采取欧美公认的0.5这一数值。根据两类上市公司2013、2014年报的流动性负债（短期）、非流动性负债（长期），可计算得出两类公司两年的违约点如表4所示：

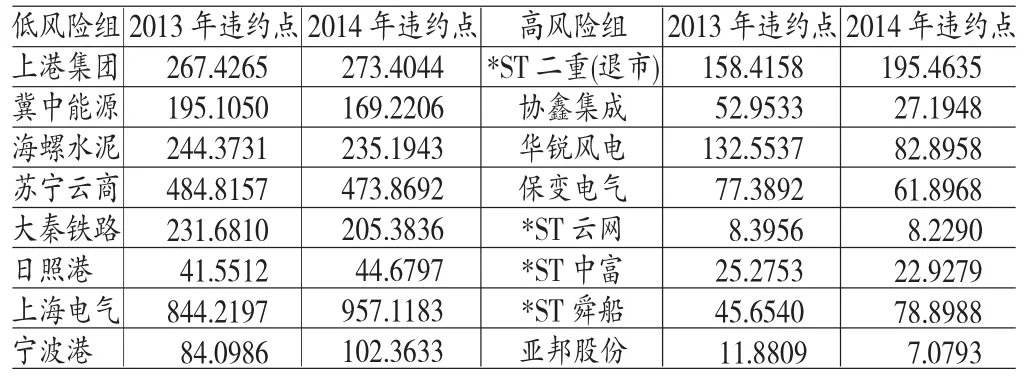
表4 2013～2014年两组公司违约点（单位：亿元）

（三）模型运算根据以上5个输入变量，联立非线性方程组。该方程组用Matlab的fslove函数通过连续牛顿迭代法求出高精度近似解。作为资产的价值VA，取值一般介于几十亿到上百亿数量级，而收益波动率σA通常在0到2之间，两者数量级相差巨大。用fslove函数迭代法计算时须将VA利用D进行标准化，引入参数EtoD=E/D。把VA=x×E代入KMV方程组，并引入EtoD=E/D化简方程组：

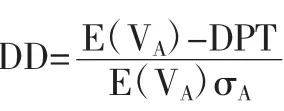
表5 2013～2014年两组公司的违约距离（DD）

为检验两组违约距离是否有显著性差异，用Matlab对两组上市公司2013～2014年的违约距离作统计检验。用单因素方差分析检验两组数据的均值是否有显著性差异，得到如表6、表7的结果。

表6 2013年两组公司统计分析结果

表7 2014年两组公司统计分析结果

由表6、7可知，2013年两组数据的P值大于0.05，从信用风险角度的判断，高风险组与低风险组的违约风险差异不显著。2014年两组数据P值小于0.05，说明高风险组的违约距离与低风险组违约距离差异明显，据此判断2014年高风险组的所有样本存在违约风险。

四、结论与建议

（一）结论本文用KMV模型预测了两组上市公司2013、2014两年信用风险。在样本组的选择上，选取了近几年属于实质性违约的8只债券。对照组选择了和样本组同一时期发行的信用评级较高的公募信用债券。用KMV模型来计算两组公司的违约距离，以此来度量各只债券在不同年度的信用风险。

从两组样本之间违约距离的均值的显著性来看，2013年两组数据之间违约风险差异不明显，2014年度两组之间出现了显著的差异，表明样本组即“高风险组”违约的可能性大增。这一预测结果与从2014年开启、2015年集中爆发的债务风险事件相符。

从单个公司动态监控的角度来看。比如模型计算的“*ST舜船”公司2013～2014年的违约距离从0.34降低到了-0.44，KMV模型暗示截至2014年底该公司所有的资产已经不能偿还负债，2015年11月该公司多笔贷款逾期且多项资产被查封，其发行的“12舜船债”面临严重的信用风险，KMV模型提前近一年预测得到了不良的后果。其他债券也可以做类似分析。

综上，无论从组别之间的对比，还是单个公司的微观角度来看，KMV模型对债券违约均有较好的预测效果。利用模型作预测，既要关注高风险和低风险组之间的对比，还要关注同一家公司在不同年份违约距离的变动趋势，以此考查信用风险变动。

（二）建议

打破“刚性兑付”传统，培育公司及其债权人风险意识。在我国的“刚性兑付”政策引领下，投资者只追求收益忽视了风险。当前我国经济下行的背景下，“刚性兑付”一方面导致无风险利率被无形推高，逐利资本逆向选择，市场资金配置失灵；另一方面债券市场的“刚性兑付”造成债务风险的不断积累。监管层应引导信用风险及时暴露，让债券市场真正做到风险和收益相匹配，改变债券市场重销售、轻风险的不良理念。

积极开发金融新产品，为投资者提供更多的风险对冲工具。随着经济下行的加深，2014年以来债券违约事件频发，需要更多措施防范债券违约风险的发生。2015年11月，国家发改委下发文件鼓励债券再担保业务，表明政策上开始准备新的风险对冲工具来应对债券违约风险。在此笔者认为，由买家定期向卖家支付一定的保费，债券违约时买方有权将债券以面值转让给卖方的CDS（信用违约互换合约），可考虑引入推广。

运用KMV模型，不断改进加强检测方式，防患于未然。从KMV模型的输入变量来看，最终影响偿债能力的因素包括：无风险利率、长短期负债结构、股权价值波动率、公司的股权价值。其一，在全球低利率的大背景下，我国货币政策也日渐宽松，无风险利率随之下降。其二，我国公司债券市场在扩容，企业长期固定利率融资增加，其长短期负债结构随之发生改变。此外，我国的股票市场投机性较强，市场在不同时期波动大、不稳定。因此KMV模型进行风险度量时需要增加检测频率，才能消除时间跨度过大、输入变量变化频繁而产生的偏差。

［1］陈晓红、张泽京、王傅强：《基于KMV模型的我国中小上市公司信用风险研究》，《数理统计与管理》2008年第1期。

［2］刘澄、张玲：《KMV模型在中国的适用性研究》，《金融纵横》2013年第10期。

［3］张玲、张佳林：《信用风险评估方法发展趋势》，《预测》2000年第4期。

［4］薛锋、董颖颖、石雨欣：《上市公司违规行为对违约距离和预期违约率影响的实证研究—兼论KMV模型的修正》，《经济管理》2005年第10期。

［5］史小坤、陈昕：《商业银行信用风险管理的KMV模型及其修正》，《南京财经大学学报》2010年第4期。

（编辑 成方）