大口径SiC非球面范成精密磨削方法及其工艺
胡德金
(上海交通大学 机械与动力工程学院, 上海 200240)
大口径SiC非球面范成精密磨削方法及其工艺
胡德金
(上海交通大学 机械与动力工程学院, 上海 200240)
为了提高大口径轴对称SiC非球面磨削的精度和效率,提出了一种基于法线跟踪的非球面范成摆动精密磨削方法,设计了运动控制模型,在磨削过程中,使砂轮主轴旋转中心线与非球面母线上磨削点法线始终保持重合。在此基础上,进一步设计了可以对非球面母线上磨削点进行实时检测的装置,建立了实现砂轮磨损自动补偿的数学模型和相关磨削工艺。研究结果表明:该方法可以避免磨削运动轨迹原理误差,运动机构简单,运动精度得到保证;应用砂轮端面进行磨削,提高了磨削比和磨削效率。
机械制造工艺与设备; 大型SiC非球面; 范成磨削; 法向跟踪; 实时检测
0 引言
为了获取更大的空间信息,大型望远镜、空间相机等系统的光学镜口径越来越大,整体非球面光学镜口径已达数米,在大型望远镜系统中,8 m以下采用整体镜面,10 m以上采用拼接技术[1]。
SiC材料由于优良的综合物理性能,现越来越多地被用来制作大型非球面光学元件,SiC材料的莫氏硬度在9~9.5之间,约低于金刚石硬度,但比微晶等光学玻璃要硬很多,加工非常困难。
对于有色金属、部分晶体非球面光学元件的加工,可以采用金刚石超精密车削来完成;对于硬脆材料的非球面加工,主要采用数控研磨成型、离子束抛光、磁流变抛光等加工方法。
SiC材料非球面光学元件的加工一般包括磨削、研磨、抛光等加工工艺。抛光工艺主要目的是改善表面粗糙度,如果用抛光工艺来改变面形精度较差的型面,将耗费大量时间,是不经济的。由于前道工序的加工精度的差异,使得许多大型非球面元件加工需要长达数月甚至数年的修磨和抛光才能达到所需面形精度和表面粗糙度,据悉,加工口径φ800 mm的SiC非球面镜的时间长达8个月。
磨削加工具有效率高、精度高优点,通过精密磨削加工使非球面元件的面形精度接近最终加工要求,从而减少抛光工艺阶段的加工余量,达到提高面形精度和表面质量的同时提高加工效率。因此,国内外众多科技工作者把精密磨削技术作为硬脆材料非球面加工的重要手段来研究。
Kuriyagawa等[2]提出了一种非球面陶瓷镜的磨削新方法,称为AEGM,主要原理如图1所示:应用金刚石砂轮的环面圆弧通过包络线对陶瓷材料非球面进行磨削,他们认为该方法提高了砂轮的寿命和加工性能,同时降低了生产成本。

图1 圆弧包络线磨削方法Fig.1 Arc envelope grinding method
目前,对凹状轴对称非球面元件加工多数采用圆弧砂轮或圆柱砂轮的部分圆弧来磨削(见图2)。文献[3]应用圆弧砂轮,通过x、y两轴联动和误差补偿技术来实现回转非球面的精密磨削加工。

图2 3种非球面磨削方法Fig.2 Several grinding methods of aspheric surface
但是,应用这些方法来磨削大口径的非球面存在一个很重要的问题,就是这些方法中的砂轮有效工作面积与被磨工件的加工面积要小很多,砂轮磨损以及磨削效率都存在需要进一步解决的问题。
为了解决大口径非球面SiC反射镜加工过程中材料去除效率与加工精度之间的矛盾,文献[4]提出了组合加工技术,对一块φ2 040 mm口径非球面SiC反射镜进行研磨。以其中一次加工周期为例介绍了组合加工技术在大口径非球面SiC反射镜加工过程中的应用。经过一次完整的组合加工过程,工件表面面形误差峰谷值由8.72 μm收敛至4.91 μm,均方根值由0.91 μm收敛至0.52 μm.
文献[5]认为:超精密磨削成形的研究工作涉及以下四方面的工作:1)高刚度、高精度磨削机床的设计和研制,包括磨削系统所需的温控、防微震、低扰动系统的设计与控制;2)非球面成形拓扑与数控策略,包括非球面补偿算法与控制;3)非球面高精度在位测量技术;4)工具控制技术等。
1 大口径非球面范成磨削方法原理
1.1 小口径非球面范成磨削方法原理
本文提出了一种基于法向跟踪的、以圆筒砂轮端面进行磨削的球面和非球面加工方法[6-7],这是一种以范成摆动球面磨削方法来实现轴对称非球面的磨削。磨削过程中,摆动中心和球心始终重合在对称轴上,砂轮主轴的旋转中心线与非球面母线上磨削点法线始终保持重合,以圆筒砂轮端面进行磨削。
如图3所示,以磨削旋转抛物面为例,设旋转抛物面母线K的方程为
y=px2,
(1)
式中:p为抛物线特征参数。

图3 非球面磨削原理图Fig.3 Schematic diagram of aspheric surface grinding
抛物面顶点在工件坐标系Oxyz的原点O上。在Oxy坐标平面内抛物线K上做点M(x0,y0)的法线,该点的曲率半径为

(2)
取M(x0,y0)点法线与y轴的交点P1(0,y1)为圆心,以P1M为半径做圆弧K′. 由法线方程可求得圆弧K′圆心P1(0,y1)在y轴上的坐标值,即

(3)


(4)
比较(2)式和(4)式,可以看出,R<|P2M|,即在母线的任何一点上由圆筒砂轮磨削形成球面的半径始终比该点抛物面母线曲率半径小。于是,就可以选择适当直径的砂轮磨具、采用范成摆动磨削球面的方法来磨削旋转抛物面。与球面磨削不同的是磨削半径R、摆动角度α和摆动中心P1(0,y1)都随x变化而变化。该磨削方法在理论上不存在加工误差,选择合适的圆筒砂轮直径,不会发生磨削干涉现象。不需要对砂轮形状做任何修整,只需要配合一定的检测手段补偿圆筒砂轮长度方向的磨损,就可以持续进行磨削,磨削效率得到了较大提高。
上述方法由于摆动中心始终在对称轴上,摆动半径受到一定限制。
1.2 大口径非球面范成磨削方法原理
一般认为,口径大于φ500 mm的非球面属于大型非球面,采用上述范成摆动方法磨削大口径非球面将使砂轮主轴的摆动半径|P1M|更大,如果砂轮主轴摆动中心定位在非球面的对称轴上,由于摆动半径太大而使结构刚性受到影响。基于上述考虑,本文在上述方法的基础上提出采用坐标平移和法向跟踪方法来解决此问题,即砂轮主轴摆动中心通过x、y两个直线运动和1个摆动运动来实现轴对称大口径非球面的范成摆动磨削加工。
图4为大口径轴对称非球面磨削原理图。图4中,设O′为磨削系统的砂轮主轴摆动中心, 并在工件坐标系Oxyz的Oxy坐标平面内平移,砂轮主轴中心线绕O′做往复摆动。砂轮主轴中心线延长线与工件坐标系Oxyz的y坐标轴相交于P1(0,y1)点。控制摆动角α,使砂轮主轴旋转中心线与非球面母线上点M(x0,y0)的法线始终保持重合。从图4可见,砂轮主轴的摆动角α即为非球面母线在点M(x0,y0)处的切线倾角,即
α=actan(f′(x0))=actan(2px0).
(5)

图4 大型非球面磨削原理图Fig.4 Schematic diagram of large aspheric surface grinding
在图4所示磨削状态,磨削运动沿非球面母线按x0正方向进给,随着工件的旋转在非球面工件上就形成螺旋上升的球面带,球面带的宽度即为圆筒砂轮直径|AB|,球面半径为|P1A|,即圆弧K′的半径R. 因为圆弧K′与非球面母线K在点M(x0,y0)相切,所以|P1A|=|P1M|=R.
又,在直角三角形△P1DA中


(6)
式中:|P1O′|为砂轮主轴摆动中心O′的运动参数;|AB|为圆筒砂轮直径;|O′C+CD|为砂轮主轴摆动中心O′到砂轮端面中心点D的距离,其中|O′C|为砂轮主轴结构参数,|CD|为圆筒砂轮长度。
令L=|P1O′|,把(4)式代入(6)式中,得
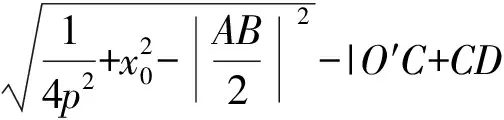
(7)
进一步算出砂轮主轴摆动中心O′的x、y坐标为
x=Lsinα,
(8)

(9)
于是,根据非球面母线方程(1)式和(5)式、(7)式、(8)式、(9)式就可以计算出磨削主轴系统的砂轮主轴摆动中心O′在工件坐标系Oxyz的Oxy坐标平面内的坐标位置,以及砂轮主轴摆动角α,从而使砂轮主轴旋转中心线与大口径旋转抛物面母线磨削点法线始终保持重合,按范成摆动球面磨削方法原理进行大口径非球面的磨削。
2 大口径SiC非球面精密磨削工艺
2.1 磨削过程的实时检测与砂轮磨损补偿
大口径SiC非球面精密磨削的难点是:材料表面硬、磨削面积大、磨削精度高。在磨削过程中,除了磨削装备刚性、部件运动精度等因素外,砂轮的磨损是影响磨削精度的重要因素,由于被磨工件面积比圆筒砂轮直径要大得多,例如,用φ80 mm直径的圆筒砂轮去磨口径φ800 mm的大型非球面,其面积相差数百倍。从大型非球面顶点到口径边缘,砂轮需经历较长的磨削行程,而且需反复进行磨削,毫无疑问, 即使采用金刚石砂轮,砂轮磨损是不可忽视的。由于砂轮磨损量的不确定性,使得磨削后非球面的面形精度就不可确定,因此,在位或实时检测技术和砂轮磨损补偿等技术是提高大口径SiC非球面器件磨削精度和效率的重要手段。
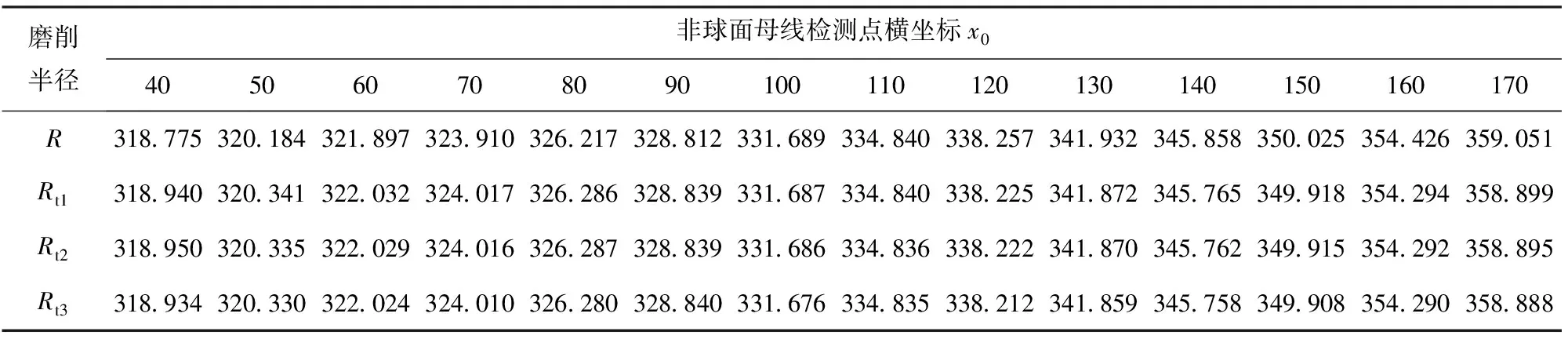
就本文提出的磨削方法而言,从(7)式可见,砂轮主轴结构参数|O′C|和圆筒砂轮半径|AD|均可视为常数。砂轮主轴摆动中心O′的运动参数L(即|P1O′|)随母线方程自变量x0、圆筒砂轮长度|CD|变化而变化,圆筒砂轮的磨损使|CD|缩短,使砂轮主轴摆动中心O′到砂轮端面中心点D的距离|O′C+CD|缩短,这就意味着磨削点偏离了理论非球面母线轨迹。要保证非球面磨削精度不受砂轮磨损的影响,就必须增加磨削主轴沿法线方向的运动距离|P1O|来补偿砂轮长度的磨损,为此,设计了一套检测方法,图5为实时检测原理图。图5中,在砂轮主轴的内部设计了一套检测装置,该检测装置既可以随磨削主轴作F1同步运动,也可以在磨削主轴内作F2独立运动。

图5 实时检测原理图Fig.5 Schematic diagram of real time detection
砂轮主轴与检测装置一体化的电主轴系统[8]如图6所示,图中圆筒形砂轮磨具与磨削主轴的中空旋转轴直接连接,检测传感器通过连接杆与安装在电主轴上端的控制器连接,控制器内装有精密的光栅尺。控制器通过连接杆推动检测传感器作上下F2运动。检测分辨率0.001 mm.
为了减少排除在圆筒砂轮内部和磨削表面的磨削液和磨削产物对检测精度的影响,在中空旋转轴中通有压缩空气。

图6 电主轴三维剖面图Fig.6 3D profile of spindle
在磨削过程中,每隔一定的时间进行检测,当检测传感器与被磨削表面接触时,控制器记录下当前磨削点的|P1M|值,设实测|P1M|=Rt,并与(4)式计算的理论R值进行比较,如果Rt (10) 实现了砂轮磨损的实时补偿。 通过检测的Rt值就可以计算出非球面母线在磨削点M的实际坐标值x0、y0,也就实现非球面母线精度的实时检测。 2.2 砂轮主轴与砂轮结构参数设计 在砂轮主轴扭矩足够大的情况下,用较大直径砂轮磨削非球面可以提高磨削效率,当然,前提是不产生磨削干涉。由于非球面母线上各点的曲率半径随着自变量x0增加而增加,当x0=0时,从(2)式和(4)式中可以看出,这时球面磨削半径与非球面曲率半径相等,球心与曲率中心重合,曲率半径最小,在这种情况下选用的砂轮几何参数毫无疑问可以适用于非球面母线上其他点的磨削。 在极端情况下,砂轮主轴摆动中心O′的运动参数R1(|P1O′|)为0,即,砂轮主轴摆动中心O′(x,y)与球心P1(0,y1)、曲率中心P2(0,y2)重合,则(7)式为 (11) 整理后 (12) 从(12)式可以看出,采用本文提出的方法磨削非球面时,圆筒砂轮直径|AB|与非球面母线焦点参数p、砂轮主轴结构参数|O′C|、圆筒砂轮长度|CD|均有关系。由(12)式可以计算出合适直径的砂轮来磨削。当然,考虑到砂轮主轴电机功率、砂轮主轴结构刚性,砂轮主轴摆动中心O′的运动参数L的运动范围等因素,避免因砂轮直径的大小而引起磨削干涉等现象产生。 2.3 非球面磨削过程的优化控制 实现大型非球面法向跟踪精密磨削的自适应控制过程如下: 1)通过(1)式自变量x确定y; 2)通过(5)式确定砂轮主轴摆动角度α; 3)检测圆弧半径R,计算砂轮磨损量; 4)通过(10)式、(8)式、(9)式确定砂轮主轴摆动中心O′在Oxy坐标平面内的x和y坐标。 法向跟踪非球面磨削与球面磨削最大区别是:非球面磨削曲率半径随着磨削进给路径不断在变化。如果在在数控系统中对几个数学模型进行编程,运算工作量大,加工速度将受到影响。为了提高加工速度,可以在计算机平台上通过编程软件按数学模型计算出加工坐标数据,然后在数控系统上运行,加工速度可以大大提高。 为了控制方便,图4所示的大型非球面工件坐标系Oxyz的y轴与机床旋转工作台的中心线重合。工件坐标系Oxyz的坐标原点O与非球面顶点重合,在这个坐标系内,x、y、α的运动关系始终是保证砂轮主轴中心线与非球面母线上磨削点法线重合。这样在从非球面顶点到口径边缘的每一次磨削循环中,始终按同样数据进行控制,即每一次磨削循环中磨削路径始终在相同的非球面母线上运动。 每循环一次,整个工件坐标系Oxyz朝机床工作台台面方向进给一次,直至磨削余量结束。 2.4 SiC非球面的研磨 磨削的目的是去除大量的加工余量,达到一定的磨削精度,要进一步提高精度和改善表面粗糙度,还需要通过研磨和抛光工艺来完成。目前,非球面计算机控制光学表面成型(CCOS)技术及抛光技术的理论基础多数都是基于Preston模型: (13) 式中:K为比例常数,与工件材料、磨粒磨料有关;v为磨削点的瞬时速度;pi为磨削点的瞬时压强。因此知道了某一点的速度和压强以及作用时间就可以计算出被抛光物件表面材料的去除量。 为了实现研磨速度和压力的控制,把图7所示电主轴前端的圆筒形砂轮磨具更换为如图7所示的研磨工具,图7中,研磨头滑动安装在连接套中,连接套固定安装在电主轴系统的中空旋转轴前端,压力弹簧紧压在研磨头上。在研磨过程中检测传感器检测研磨头的位移,根据压力弹簧的特性曲线和研磨头端面面积就可以计算出研磨头端面上的压强。磨削点瞬时速度可以从数控系统中设定的转速、进给速度、摆动速度来确定。 图7 研磨工具Fig.7 Polishing tool 研磨过程同样根据非球面母线方程(1)式和(5)式、(8)式、(9)式、(10)式进行计算,所不同的是(10)式中的砂轮磨损量Δw变成了研磨头端面研磨压强pi的控制参数,Δw越大、研磨压强pi越大。 非球面精密磨削实验装备如图8所示,实验参数如下:砂轮主轴转速5 000 r/min,非球面工件转速8 r/min,非球面工件口径为φ400 mm,非球面工件材料为SiC,设非球面母线方程(1)式中p=0.001 581,粗糙度检测仪为德国Mahr公司的MarSurf PS1检测仪。 图8 实验装备Fig.8 Experimental equipment 磨削分3个阶段: 1) 第一次磨削。圆筒砂轮直径为φ80 mm,圆筒砂轮材料为陶瓷+金刚石,砂轮磨料粒度60~70,进给量0.02 mm,磨削后表面粗糙度Ra0.5~0.6 μm. 2) 第二次磨削。圆筒砂轮直径为φ60 mm,圆筒砂轮材料为陶瓷+金刚石,砂轮磨料粒度 120~120,进给量0.005 mm,磨削后表面粗糙度Ra0.2~0.4 μm. 3) 研磨。研磨盘直径为φ80 mm,研磨膏为W1000金刚石微粉,磨削后表面粗糙度Ra0.08~0.1 μm. 图9为在磨削的非球面工件照片,先用千分表检测回转精度,沿外口径处跳动≤0.008 mm. 然后通过检测系统按非球面母线方程,x0每隔10 mm在位检测Rt,分3种情况进行检测,检测结果如表1所示。表1中R为理论磨削半径,Rt1、Rt2、Rt3为在实验机床上的实际检测值。从实测数据看,在3种情况下,重复检测精度在0.01 mm左右,但与母线理论计算值相差比较大,可能因素是图6中检测传感器的原点位置与图5中的砂轮主轴摆动中点O′之间的距离存在加工制造误差所引起。 表1 非球面磨削检测数据Tab.1 Detecting data of aspheric surface grinding mm 注:Rt1为砂轮和工件均不旋转时的实测值,Rt2为砂轮转速3 000 r/min、工件不旋转时的实测值,Rt3为砂轮转速3 000 r/min、工件转速6 r/min时的实测值。 图9 磨削的SiC非球面工件Fig.9 Grinding SiC aspheric workpiece 1)基于法向跟踪的大口径轴对称非球面精密磨削方法,使砂轮主轴旋转中心线与非球面母线上磨削点的法线始终保持重合,使磨削点的运动轨迹始终保持在非球面母线上,避免了原理上误差。 2)用圆筒砂轮端面对非球面进行磨削,直径不会变化,结合实时检测与砂轮磨损补偿,减少了砂轮端面长短磨损对运动控制模型精度的影响,无需对砂轮做任何修整,可以保持长时间持续磨削。 3)用圆筒砂轮端面磨削非球面,磨削面积大,提高了磨削比,提高了磨削效率。 References) [1] 张景旭. 地基大口径望远镜系统结构技术综述[J]. 中国光学, 2012, 5(4): 327-336. ZHANG Jing-xu. Overview of structure technologies of large aperture ground-based telescopes[J]. Chinese Optics, 2012, 5(4):327-336. (in Chinese) [2] Kuriyagawa T, Zahmaty M S S, Syoji K. A new grinding method for aspheric ceramic mirrors[J]. Journal of Materials Processing Technology, 1996, 62(4): 387-392. [3] 韩成顺, 董申. 超精密磨削大型光学非球面元件的研究[J].光电工程, 2003, 30(6): 43-46. HAN Cheng-shun, DONG Shen. Study on ultra- precision grinding of large optical aspherical elements[J]. Opto-Electronic Engineering, 2003, 30(6): 43-46. (in Chinese) [4] 刘振宇. 应用组合加工技术加工2 m口径非球面碳化硅反射镜[J]. 光学学报, 2015, 35(A01): 344-350. LIU Zhen-yu. Grinding 2 m diameters aspheric SiC mirror with multi-mode optimization technique[J]. Acta Optica Sinica, 2015, 35(A01): 344-350. (in Chinese) [5] 许乔, 王健, 马平, 等. 先进光学制造技术进展[J]. 强激光与粒子束. 2013, 25(12): 3098-3105. XU Qiao, WANG Jian, MA Ping, et al. Progress of advanced optical manufacturing technology[J]. High Power Laser and Particle Beams, 2013, 25(12): 3098- 3105. (in Chinese) [6] 胡德金. 环状内外球面智能精密磨削方法与控制模型研究[J]. 兵工学报, 2015, 36(9): 1743-1749. HU De-jin. Research on intelligent precision grinding method and control model of annular inner and outer sphere[J]. Acta Armamentarii, 2015, 36(9): 1743-1749. (in Chinese) [7] 胡德金. 二次旋转曲面精密磨削原理与运动控制方法研究[J]. 机械工程学报, 2014, 50(13): 178-183. HU De-jin. Study on principle and control method for precisely grinding quadratic rotated conicoid[J]. Chinese Journal of Mechanical Engineering, 2014, 50(13): 178-183. (in Chinese) [8] 胡德金,郁翔, 李峰, 等. 精密磨削与检测一体化电主轴:中国, CN104551981A [P]. 2015-04-29. HU De-jin, YU Xiang, LI Feng, et al. Precision grinding and detection integrated electric spindle: China, CN104551981A [P]. 2015-04-29. (in Chinese) Precision Generated Grinding Method and Its Technology of Large Diameter SiC Aspheric Surface HU De-jin (School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China) In order to improve the grinding accuracy and efficiency of large diameter aspheric surface, a generated grinding method for aspheric surface based on the normal track is proposed, and a motion control model is designed. In grinding process, the rotation centerline of grinding wheel spindle always coincides with normal line of grinding point on aspheric surface. A detecting device is designed for tracking shaping precision in real-time, and a mathematical model and a related grinding process for automatic compensation of grinding wheel wear are established. Results show that the proposed method can be used to avoid the principle error of grinding motion trajectory, make the motion mechanism simple, and ensure the motion accuracy; grinding ratio and grinding efficiency are increased by using the end face of the grinding wheel for aspheric surface grinding. manufacturing technology and equipment; large diameter SiC aspheric surface; generated grinding; normal tracking; real-time detection 2016-03-15 机械系统与振动国家重点实验室基金项目(MSVZD201515) 胡德金(1947—),男,教授,博士生导师。E-mai:djhu@sjtu.edu.cn TG580.61+2 A 1000-1093(2016)12-2340-07 10.3969/j.issn.1000-1093.2016.12.021




3 实验结果分析


4 结论

