集中载荷作用下的履带车辆稳态转向分析与试验

王红岩， 陈冰， 芮强， 郭静， 史力晨

(1.装甲兵工程学院 机械工程系, 北京 100072; 2.中国北方车辆研究所 车辆传动重点实验室, 北京 100072; 3. 63963部队, 北京 100072)

集中载荷作用下的履带车辆稳态转向分析与试验

王红岩1， 陈冰1， 芮强1， 郭静2， 史力晨3

(1.装甲兵工程学院 机械工程系, 北京 100072; 2.中国北方车辆研究所 车辆传动重点实验室, 北京 100072; 3. 63963部队, 北京 100072)

为了研究集中载荷条件下履带车辆稳态转向性能，提高转向模型精度，分析了履带张力对接地压力分布的影响，推导履带车辆接地压力分布计算模型。运用履带与土壤之间的剪切应力- 剪切位移关系推导新的转向动力学模型，建立相应的动力学方程组并求解。分析了履带宽度和履带张力引起的接地压力变化对稳态转向运动学和动力学参数的影响，并通过实车试验测试对分析结果进行验证。结果表明，理论计算结果与试验数据有很好的一致性，验证了该模型的正确性。

兵器科学与技术； 履带车辆； 集中载荷； 履带张力； 稳态转向

0 引言

早在20世纪国外学者就对履带车辆的转向问题展开研究，前苏联学者针对工程应用[1]中忽略履带滑移和滑转，分析履带车辆转向特性并进行理论计算，得到简单但实用的计算公式。然而履带车辆转向过程始终伴随着两侧履带的滑移和滑转，研究表明，考虑滑移、滑转条件得到的转向半径约为理论转向半径的1.5倍，转向角速度约为理论转向角速度的2/3[2]。Steeds[3]考虑车辆两侧履带的滑移滑转，认为履带接地压力均匀分布，且转向过程满足库仑摩擦原理，分析履带车辆转向。然而由于没有数字计算机的缘故，steeds采用试凑法得出近似解。Kitano等[4]考虑载荷集中分布，分析履带车辆转向数学模型，建立车辆转向的平面运动方程组，运用计算机进行运动学和动力学方程的运算。Wong等[5]结合履带地面力学，通过土壤剪切力和剪切位移关系，建立运动学和动力学方程组，分析了两侧履带牵引力、制动力以及转向阻力系数随转向半径的变化趋势，并且Wong等将计算结果与Ehlert等[6]的试验数据进行对比验证。Al-Milli等[7]研究了履带车辆在软路面稳态转向过程中转向阻力系数随转向半径的变化关系，并且进行了履带车比例模型试验。国内不少学者就履带车辆转向进行了研究。曹付义等[8]通过对履带车稳态转向接地段履带剪切位移的引入，建立了履带车辆软地面转向驱动力计算模型并进行仿真分析。迟媛等[9]分析了重心偏移对履带车辆转向时最大驱动力的影响，并进行了实例计算与对比分析。文献[10-11]采用数值迭代的方法计算转向运动学和动力学特性并进行实车试验。

本文主要分析了履带张力对接地段压力分布影响，在此基础上建立新的转向动力学模型，分析履带板宽度和履带张力改变接地压力分布形式时对履带车辆转向运动学和动力学参数的影响，并进行实车试验以及模型验证。

1 接地压力模型

履带车辆接地压力分布影响着履带与地面之间的剪切应力，从而影响履带车辆牵引力、制动力以及转向阻力矩等性能参数。研究表明，履带接地压力分布形式受到负重轮数量、负重轮分布位置等车辆设计参数以及土壤介质等因素的影响[12]，因此履带接地压力模型必须结合实车试验进行分析。图1是接地压力试验测试系统，试验过程中传感器信号的接收和初步处理由美国国家仪器公司(NI)测试系统完成，试验采用的应变式负荷传感器相关参数如表1所示。

采集多组试验测试数据得到履带车辆接地压力分布如图2所示。从图2中可以看出，履带车辆低速直线行驶速度为v，T为履带张力，诱导轮与最后一个负重轮之间的后支履带处于张紧状态，并且接地压力主要集中在负重轮正下方。文献[13]中假设履带车辆接地压力呈倒三角形分布于各负重轮正下方，并建立牵引力与滑转率关系的计算模型。然而计算过程过于复杂，为了提高模型计算效率，本文提出了负重轮正下方接地压力呈矩形分布形式如图3所示，并进行履带车辆地面牵引力与滑转率关系试验，图3中数字1，2，…，6分别代表各负重轮受到接地压力的覆带板。

图1 接地压力试验测试系统Fig.1 Load distribution test system

参数数值传感器标定值标准值/kN加载输出/V卸载输出/V量程/kN30000020005输出电压/V0～5610011000供电电压/V241220022001综合精度≤01%F．S1830033002工作温度/℃-20～602440044003测试温度/℃-10～603050055004

图2 试验测试接地压力分布Fig.2 Test load distribution

图3 接地压力矩形分布Fig.3 Rectangle shape of load distribution

图4是地面牵引力与滑转率关系试验的试验车与负载车，两车之间的拉力由连接试验车辆和负载车辆的拉力传感器测得，并且通过与行驶阻力相加得到履带与地面之间的牵引力。负载车通过变换不同制动强度，使试验车辆履带与地面产生不同程度的滑转。

图4 试验车与负载车Fig.4 Test vehicle and laden vehicle

图5为牵引力与滑转率关系曲线。从图5中可以看出，倒三角形和矩形两种接地压力分布方式的地面牵引力与滑转率曲线和试验数据都十分接近。为了简化计算可以认为履带接地压力呈矩形集中分布于负重轮正下方。

图5 牵引力与滑转率关系曲线Fig.5 Traction vs. slippage rate

由于履带车辆行驶时始终存在履带张力作用，使得每个重轮正下方压力值有所变化。履带张力主要包括：工作张力、预紧张力和离心张力。由于履带车辆进行低速稳态行驶，离心张力很小，对接地压力分布影响也很小；预紧张力即诱导轮施加给履带的张紧力，对履带车辆接地压力分布影响也不显著；工作张力是履带车辆行进过程中由于牵引力、制动力使得履带绷紧产生的张力，对接地压力分布有显著影响。因此本文中所描述的履带张力主要考虑了工作张力对接地压力分布的影响。假设履带张力产生的压力变化集中分配于负重轮正下方如图6所示，其中G为车重，n是单侧履带负重轮数，l是履带板节距，L是履带接地长度，pnc,s是不考虑履带张力各负重轮下方的接地压力，αs是履带张力引起的接地压力变化量，并根据文献[4]假设αs按照一定的线性规律变化，λ是履带张力引起压力变化部分的斜率，T是履带张力，t是履带张力垂直地面分量，θf为离去角，且满足关系式t=Tsinθf. 则履带负重轮下方压力变化量pc,s服从如下分布：

(1)

式中：b为履带板宽度。

图6 履带张力作用接地压力分布Fig.6 Load distribution induced by track tension

履带车辆低速直线行驶过程中，履带车辆所受力和力矩处于平衡状态，根据车重与轮荷之间的平衡关系以及车重和各轮荷对履带与地面的接触点M力矩平衡可得

(2)

(3)

由(1)式、(2)式、(3)式即可以得出履带张力作用下负重轮的压力变化量pc,s为

(4)

因此可以得出考虑履带张力时接地压力分布如图7，且满足以下表达式：

piT(s)=pnc,s+pc,s,i=1,2,

(5)

式中：1代表内侧履带，2代表外侧履带；s=1,2，…，6.

图7 考虑履带张力后接地压力分布示意图Fig.7 Schematic diagram of load distribution in considering track tension

综上分析可以看出，图7中的接地压力分布形式与图2中的试验测试结果基本一致。

2 转向模型建模

2.1 假设条件与坐标系建立

1)履带车在硬质沙土路面作稳态转向运动，不考虑履带的沉陷和推土效应。

2)履带与土壤之间的剪切力与该点剪切位移相关，并且满足关系式：τ=τmax[1-exp (-j/K)], 其中K是土壤抗剪切模量，j为土壤的剪切位移。

3)履带车辆转向过程中，履带与地面之间的摩擦系数为常数，且符合库仑定律。

4)履带车辆转向过程中行驶阻力系数与直线行驶时相同。

图8 转向模型坐标系Fig.8 Coordinate system of tracked vehicle

2.2 转向运动学分析

履带车辆稳态转向时，履带与地面之间不可避免会产生滑移和滑转。图9是履带车辆稳态转向的运动关系图。

图9 履带车辆转向运动学关系Fig.9 Steering kinematics relation of tracked vehicle

假设任一点(xi，yi)处剪切速度为vj1，通过坐标系之间变换可得速度在惯性坐标系下X、Y方向分量为

(6)

(7)

t0是履带车辆稳态转向过程中由起始点行驶至yi处的时间：

t0=(L/2+cy-D-yi)/(rdωi),

(8)

式中：rd为驱动轮半径；ωi为驱动轮角速度。

履带与土壤的剪切位移在惯性坐标系中X、Y方向分量可表示为

jXi=(R′∓B/2+cx+xi)(cosφi-1)-yisinφi,

(9)

jYi=(R′∓B/2+cx+xi)sinφi-(L/2-D+cy)+

yicosφi.

(10)

对任一点(xi，yi)处的剪切位移可以表示为

(11)

2.3 转向动力学分析

考虑离心力CF作用两侧履带的负荷N1、N2将重新分配，两侧履带接地压力也会发生变化。两侧履带接地段法向负荷和接地压力服从以下规律：

(12)

(13)

式中：h为履带车重心高度。履带车辆转向时，外侧履带牵引，履带与地面之间产生滑转，诱导轮与负重轮之间的后支履带张紧。内侧履带制动，履带与地面之间产生滑移，主动轮与负重轮之间的前支履带张紧。由前述分析可知，在两侧履带张力作用下接地压力分布形式有所不同，如图10所示。

图10 履带车辆转向接地压力分布Fig.10 Steering load distribution of tracked vehicle

因此在同时考虑离心作用和履带张力时，两侧履带接地压力分布服从以下变化规律：

(14)

(15)

履带车在硬质沙土路面行驶时，履带接地段剪切力与剪切位移满足如下关系式：

τ=pμ[1-exp (-j/K)],

(16)

式中：p为履带板与地面之间的正压力；μ为履带与地面之间的摩擦系数。

图11是履带车辆转向的动力学关系图。由图11可知，Fx1、Fx2、Fy1、Fy2分别是履带车辆两侧履带的剪切力在牵连坐标轴下x方向和y方向的分量，Mμ1、Mμ2分别为两侧履带转向阻力矩，Rf1、Rf2分别为两侧履带行驶阻力，CF为离心力。履带板接地压力段单位面积内的剪切力，以及两侧履带的牵引力和制动力表示为

dF=τdA=pμ(1-e-ji/K)dA,

(17)

(18)

(19)

图11 履带车辆转向动力学关系Fig.11 Steering dynamics relation of tracked vehicle

转向驱动力矩以及转向阻力矩表达为

μ(1-e-ji/K)sinδidxdy,

(20)

(21)

cosδidxdy,

(22)

(23)

2.4 运动学方程求解

履带车辆稳态转向过程中x、y方向作用力以及作用力对o点力矩平衡方程为

(24)

图12是稳态转向模型求解流程图，当给定履带车辆结构参数b、h、l、B，地面参数K、μ、f，转向速度v、相对转向半径ρ时，通过对以上3个方程求解可以得出履带车辆两侧驱动轮转速rdω1、rdω2和相对转向极纵向偏移量D. 最后将得到的解代入以上公式，则可以得到履带车辆稳态转向运动学和动力学参数与相对转向半径的关系。

图12 转向模型求解流程Fig.12 Solving flow chart of steering of tracked vehicle

3 稳态转向性能分析

由以上分析可知履带宽度、履带张力对滑移率和滑转率、牵引力和制动力以及转向阻力矩有影响。

3.1 履带宽度对牵引力、制动力的影响

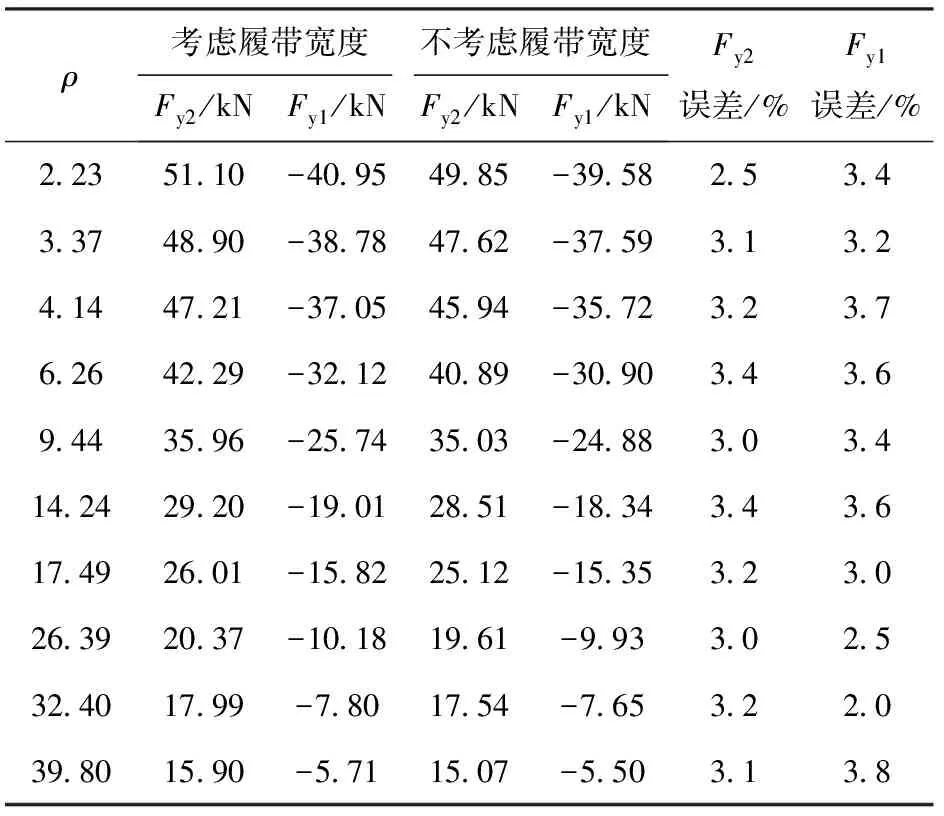
图13给出了履带宽度对两侧履带牵引力Fy2和制动力Fy1的影响。从图13中可以看出，与不考虑履带宽度情况相比，考虑履带宽度时牵引力和制动力有所偏大。表2是计算结果。从表2中可以得出两种情况下牵引力和制动力的模型计算值相差不大，牵引力误差范围在2.5%～3.4%，制动力误差范围在2.0%～3.8%. 因此，认为履带宽度对转向性能的影响可以不予考虑。

图13 履带宽度对牵引力和制动力的影响Fig.13 Influence of track width on traction and braking force

ρ考虑履带宽度不考虑履带宽度Fy2/kNFy1/kNFy2/kNFy1/kNFy2误差/%Fy1误差/%2235110-40954985-395825343374890-38784762-375931324144721-37054594-357232376264229-32124089-309034369443596-25743503-2488303414242920-19012851-1834343617492601-15822512-1535323026392037-10181961-993302532401799-7801754-765322039801590-5711507-5503138

3.2 履带张力作用对滑移率和滑转率的影响

滑移率σ1和滑转率σ2分别表示两侧履带发生滑移和滑转的程度。图14(a)、图14(b)分别给出了履带张力作用对滑移率和滑转率的影响。由图14(a)可知考虑履带张力作用时，内侧履带接地压力分布有明显的变化，滑移率变大，并且当相对转向半径在1～10的范围内时差异明显，误差范围在20%～30%. 从图14(b)可以看出，两种情况下滑转率计算曲线基本重合，可见履带张力作用对外侧履带滑转率影响不大。

图14 滑移率、滑转率与相对转向半径关系Fig.14 Relationships among σ1, σ2 and ρ

3.3 履带张力作用对牵引力、制动力以及转向阻力矩的影响

图15给出了履带张力对牵引力和制动力的影响。从图15中可以看出，考虑履带张力条件下，由于两侧履带第一个和最后一个负重轮下方接地压力减小，两侧牵引力、制动力总体相对偏小，在相对转向半径在1～10的范围内，履带张力作用对牵引力和制动力的影响相对明显。

图15 履带张力对牵引力、制动力影响Fig.15 Influence of track tension on traction force and braking force

图16 履带张力对转向阻力矩影响Fig.16 Influence of track tension on steering resistance torgue

图16给出了履带张力作用对转向阻力矩的影响。从图16中可以看出，考虑履带张力作用时，履带两侧第一个和最后一个负重轮下方接地压力减小，形成中间接地段压力大，两端接地段压力小的分布形式。因此，转向阻力矩也相应减小。在相对转向半径为1～10范围内时，转向阻力矩减小比较明显，约为10%.

4 试验验证与分析

为了验证该模型的可信性和准确性，对履带车在硬质砂土路面进行实车转向试验，试验相关设备如图17所示，其中存储式转矩测试仪测量两侧输出轴转矩和转速。NI系统主要接收各传感器的信号，实现一般性数据的采集；GPS系统由移动站和基准站组成，主要完成运动轨迹、车速以及转向半径的测量。图18是试验数据处理流程，由于试验数据是由不同的系统测得，因此需要对数据进行同步、截断等处理，并通过运动学和动力学计算得出各转向性能参数。

图17 转向试验系统Fig.17 Steering experimental system

图18 试验处理流程Fig.18 Flow chart of data processing

图19(a)、图19(b)分别是滑移率、滑转率试验数据与模型计算结果对比。由图19(a)中可以得出考虑履带张力作用，滑移率随相对转向半径的变化曲线与试验数据有很好的一致性，而不考虑履带张力得到的曲线与试验数据有较大偏差。由图19(b)中可以看出关于滑转率随相对转向半径关系，两条计算曲线和试验数据趋势基本一致。

图19 滑移率和滑转率试验数据与计算结果对比Fig.19 Comparison of calculated and test results of skid and slippage rates

图20是处理后牵引力和制动力试验数据与模型计算结果对比，图21是转向阻力矩试验数据与模型计算结果对比。从图21中可以看出，相对于不考虑履带张力作用，考虑履带张力所得到的计算模型曲线与试验数据有更好的一致性。

图20 牵引力、制动力试验数据与计算结果对比Fig.20 Comparison of calculated and test results of traction and braking force

图21 转向阻力矩试验数据与计算结果Fig.21 Comparison of calculated and test results of steering resistance torque

通过以上滑移率和滑转率、牵引力和制动力、以及转向阻力矩的对比分析，表明本文所建模型是准确可信的。

5 结论

本文基于履带车辆硬质沙土路面接地压力试验，分析集中载荷作用下履带张力对接地压力分布的影响，推导出新的稳态转向模型。对滑移率和滑转率、牵引力和制动力以及转向阻力矩等参数进行计算，并通过试验数据验证该模型的准确性。得出结论如下：

1)分析履带宽度对牵引力和制动力的影响，结果表明履带宽度对其影响不大，二者差异在3%左右。

2)计算了履带张力作用对滑移率和滑转率的影响。当考虑履带张力作用，两侧履带滑移率和滑转率与试验测试结果有很好的一致性；不考虑履带张力作用时，得到滑移率曲线与试验数据有较大偏差。即本文所建立考虑履带张力影响的转向模型，可以比较准确地计算出履带车辆稳态转向两侧履带的滑移率和滑转率。

3)考虑履带张力对接地压力的影响，整体上牵引力和制动力以及转向阻力矩有减小的趋势。在相对转向半径为1～10时转向阻力矩减小较为明显，约为10%.

References)

[1] 闫清东, 张连第, 赵毓芹, 等. 坦克构造与设计[M]. 北京: 北京理工大学出版社, 2007: 222-232. YAN Qing-dong, ZHANG Lian-di, ZHAO Yu-qin, et al. Structure and design of tank[M]. Beijing: Beijing Institute of Technology Press, 2007: 222-232.(in Chinese)

[2] 程军伟, 高连华, 王红岩. 基于打滑条件下的履带车辆转向分析[J]. 机械工程学报, 2006, 42(增刊): 192-195. CHENG Jun-wei, GAO Lian-hua, WANG Hong-yan. Steering analysis of tracked vehicles based on skid condition[J]. Journal of Mechanical Engineering, 2006, 42(S): 192-195.(in Chinese)

[3] Steeds W. Tracked vehicles-an analysis of the factors involved in steering[J]. Automobile Engineer, 1950, 4(3): 143-148.

[4] Kitano M, Jyozaki H. A theoretical analysis of steerability of tracked vehicles[J]. Journal of Terramechanics, 1976, 13(4): 241-258.

[5] Wong J Y, Chiang C F. A general theory for skid steering of tracked vehicles on firm ground[J].Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2001, 215(3): 343-355.

[6] Ehlert W, Hug B, Schmid I C. Field measurements and analytical models as a basis of test stand simulation of the turning resistance of tracked vehicles[J]. Journal of Terramechanics, 1992, 29(1): 57-69.

[7] Al-Milli S, Seneviratne L D, Althoefer K. Track-terrain modeling and traversability prediction for tracked vehicles on soft terrain[J]. Journal of Terramechanics, 2010, 47(3): 151-160.

[8] 曹付义, 刘洋, 周志立. 履带车辆软地面稳态转向驱动力计算模[J]. 河南科技大学学报, 2014, 35(2): 29-32. CAO Fu-yi, LIU Yang, ZHOU Zhi-li. Steady turning thrust calculation model of tracked vehicle on soft terrain[J]. Journal of Henan University of Science and Technology, 2014, 35(2): 29-32.(in Chinese)

[9] 迟媛, 蒋恩臣. 履带车辆转向时最大驱动力矩的计算[J]. 农业工程学报, 2009, 25(3): 74-78. CHI Yuan, JIANG En-chen. Method for calculating maximum tractive torque of tracked vehicle while steering[J].Transactions of the Chinese Society of Agricultural Engineering, 2009, 25(3): 74-78.(in Chinese)

[10] 王红岩, 王钦龙, 芮强, 等. 高速履带车辆转向过程分析与试验验证[J]. 机械工程学报, 2014, 50(16): 162-172. WANG Hong-yan, WANG Qin-long, RUI Qiang, et al. Analyzing and testing verification the performance about high-speed tracked vehicles in steering process[J]. Journal of Mechanical Engineering, 2014, 50(16): 162-172.(in Chinese)

[11] 芮强, 王红岩, 王钦龙, 等. 基于剪切应力模型的履带车辆转向力矩分析与试验[J]. 兵工学报, 2015, 36(6): 968-997. RUI Qiang, WANG Hong-yan, WANG Qin-long, et al. Analysis and experiment of tracked vehicle steering torque based on stress model[J]. Acta Armamentarii, 2015, 36(6): 968-997.(in Chinese)

[12] Wong J Y. Theory of ground vehicles, [M]. 3rd ed. New York: John Wiley & Sons, 2001.

[13] 栗浩展, 王红岩，芮强, 等. 履带车辆地面牵引力的计算与试验验证[J]. 装甲兵工程学院学报, 2015, 29(1): 36-41. LI Hao-zhan, WANG Hong-yan, RUI Qiang, et al. Calculation method and testing verification of soil thrust of tracked vehicle[J]. Journal of Academy of Armored Force Engineering, 2015, 29(1): 36-41.(in Chinese)

Analysis and Experiment of Steady-state Steering of Tracked Vehicle under Concentrated Load

WANG Hong-yan1， CHEN Bing1， RUI Qiang1， GUO Jing2， SHI Li-chen3

(1.Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072， China;2.Science and Technology on Vehicle Transmission Laboratory, China North Vehicle Research Institute, Beijing 100072， China;3.Unit 63963 of PLA, Beijing 100072， China)

In order to study the steady-state steering performances of tracked vehicle under concentrated load and improve the simulating accuracy of tracked vehicle steering model, the effect of track tension on ground pressure distribution is analyzed, and a computation model of ground pressure distribution of tracked vehicle is proposed. A new steering dynamics model is derived to establish a corresponding dynamics equation set based on shear stress and shear displacement relationships of track and ground. The effect of ground pressure change induced by track width and tension on steady-state steering kinematics and dynamics parameters is analyzed. The analysis result is verified through vehicle test. The test results show that the theoretically calculated result is well fitted with the test data, and the proposed model is proven to be effective.

ordnance science and technology; tracked vehicle; concentrated load; track tension; steady-state steering

2016-05-03

军队科研计划列支项目(2014WX04)

王红岩(1965—)，男，教授，博士生导师。E-mail: why_cvt@263.net

TJ811

A

1000-1093(2016)12-2196-09

10.3969/j.issn.1000-1093.2016.12.003