基于解析法的电磁发射弹丸内膛磁场分布特性分析
李湘平, 鲁军勇, 李玉, 武晓康
(海军工程大学 舰船综合电力技术国防科技重点实验室, 湖北 武汉 430033)
基于解析法的电磁发射弹丸内膛磁场分布特性分析
李湘平, 鲁军勇, 李玉, 武晓康
(海军工程大学 舰船综合电力技术国防科技重点实验室, 湖北 武汉 430033)
电磁轨道发射装置膛内的磁场分布特性对制导弹丸的器件布局设计非常重要。对电磁轨道发射装置膛内的强磁场环境进行了分析,基于毕奥- 萨伐尔定律推导了考虑弹丸运动位移和电流趋肤深度下膛内磁场的计算公式。通过时谐分析方法并采用数据拟合的方式得到了电感梯度与电流频率和弹丸运动位移的函数关系,用以分析弹丸的内弹道运动特性。采用时频分析方法得到了电流趋肤深度随时间的变化关系,从而建立了弹丸中轴线磁场分布特性求解的三维解析计算模型。以实验室的电磁发射装置为例,采用试验电流数据作为输入,对内膛弹丸处磁场分布特性进行解析计算。结果表明:弹丸中轴线的磁感应频率在450 Hz以下,磁感应强度峰值达到0.4 T,并沿弹丸长度方向迅速衰减,100 mm处的磁场基本降为0. 利用磁探针的测试数据验证了理论计算模型的正确性。
兵器科学与技术; 电磁发射; 内膛磁场分析; 毕奥- 萨伐尔定律; 电流趋肤效应; 时谐分析; 时频分析
0 引言
相比常规弹药,电磁轨道发射弹丸以电能为发射能源,利用电磁力推动弹丸加速,突破了常规火炮的初速限制,具有初速高、射程远、发射成本低等优越性[1]。同时,一体化弹丸由于具有体积小、超高声速的特点,是一种易攻难防、攻防兼备的新概念武器,有很广泛的作战应用需求,主要用于打击水面舰艇、远程火力支援以及防空反导等[2-3]。电磁轨道发射装置的工作原理图如图1所示。

图1 电磁发射工作原理图Fig.1 Schematic diagram of electromagnetic launcher
图1中电枢用于连通两根导轨的电流,并与导轨和脉冲电源一起构成一个闭合回路。受洛仑磁力的作用,电枢沿导轨方向滑动,并推动弹丸往前运动。由于激励电流一般到兆安级,发射装置膛内的磁场达到几十特斯拉,频率在几千赫兹以下,低频强磁场会带来制导弹丸内部引信安全性问题、制导控制系统中的磁敏感器件失灵、舵机失效等问题[4]。
在电磁发射过程中,弹丸内部的磁场分布特性受激励电流、导轨电感梯度、弹丸运动速度等因素的影响,磁场分布较为复杂。目前研究人员对电磁轨道发射装置的各项性能指标,如导轨和电枢电流分布特性[5]、导轨电感梯度[6-7]、发射装置膛内磁场分布特性[8]、弹丸内弹道运动[9-10]等进行了大量的仿真分析和试验研究。文献[5]采用有限差分的方法,得到了二维情况下的导轨和电枢上的电流分布,但不能适用于三维情况。文献[6-7]分别采用理论推导和有限元仿真的方法对电感梯度进行了仿真,但文献[6]假定电流为无厚度的平面电流,忽略了电流的趋肤深度,文献[7]没有考虑电枢所在位置对电感梯度的影响。文献[8]基于毕奥- 萨伐尔定律推导了发射装置膛内磁感应强度的解析模型,但未考虑导轨电流的在4个表面的趋肤效应。文献[9-10]分析了弹丸内弹道的运行情况,但没有考虑弹丸与导轨接触的摩擦阻力。上述文献都没有立足于一体化弹丸的设计,对电枢前端弹丸位置处的内膛环境进行分析,尤其是对磁场时空分布特性的分析。本文通过建立三维理论计算模型,对弹丸中轴线上的磁感应强度进行了解析计算,并利用磁探针的试验数据验证了该模型的正确性,对一体化弹丸内部电子器件的布局提供了一定的设计依据。
1 计算模型
本文针对发射装置为方形口径、电枢为长方体的模型进行仿真,导轨间距h=30 mm,宽度wr=50 mm,厚度hr=20 mm;电枢长度l=30 mm,宽度wa=30 mm,其磁场坐标如图2所示。
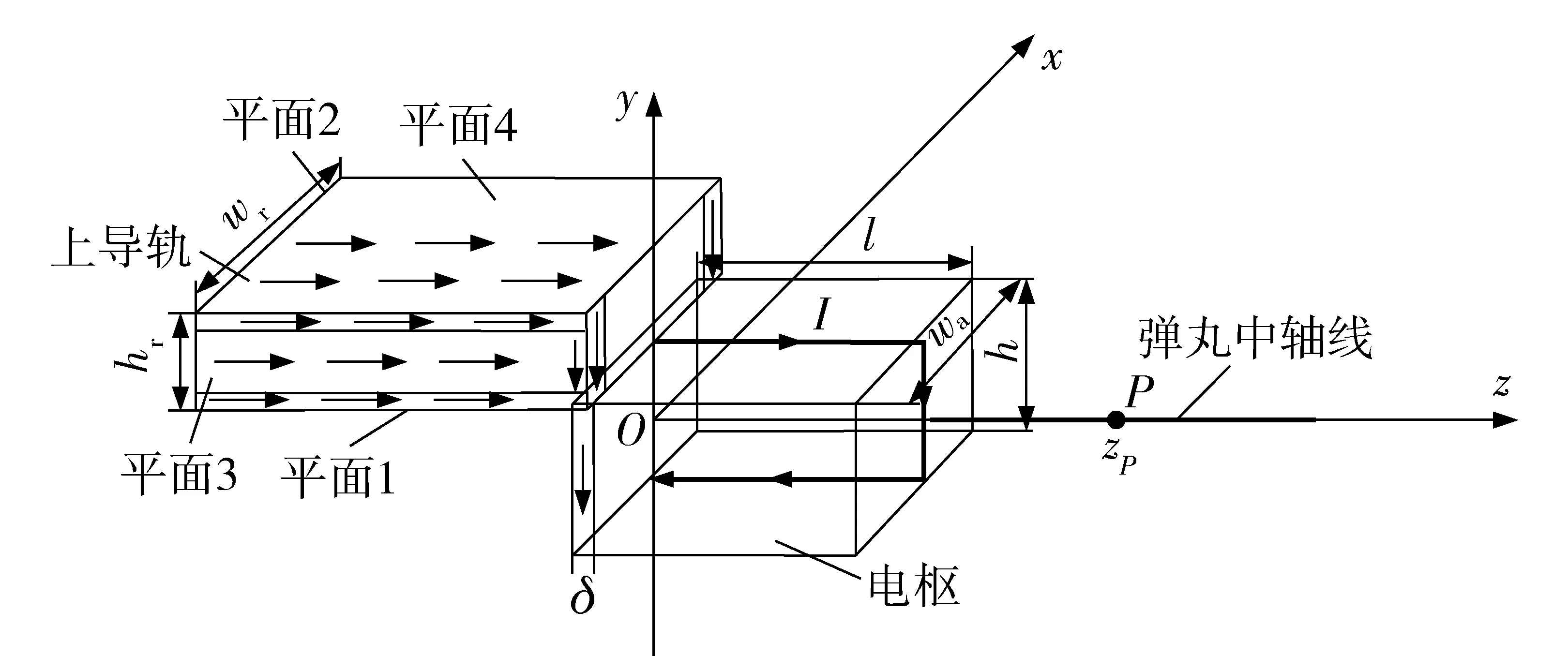
图2 发射装置磁场坐标Fig.2 Magnetic field coordinate of launcher
为了简化计算,在已知导轨输入电流曲线的情况下,对弹丸中轴线上的电磁场进行解析计算和仿真。由于导轨加载的电流一般为低频电流,变化较慢,因此可以假定在计算步长Δt内电流保持不变,从而直接利用毕奥- 萨伐尔定律计算Δt时间段内输入电流感应出的磁场。
同时,由于输入导轨的电流为交变电流,在电磁发射过程中普遍存在电流趋肤效应,考虑导轨在4个表面上都有电流分布[11]。假设流过导轨和电枢上的电流在导体趋肤深度范围内均匀分布,电流方向如图2所示。采用体电流分布的电流元形式为:
电枢电流元-JVdxdydzax,上导轨电流元JVdxdydzaz,下导轨电流元-JVdxdydzaz,ax、az表示单位向量。
电枢体电流密度JV=I/Sa,导轨体电流密度JV=I/Sr,Sa、Sr分别表示流过电枢和导轨电流的面积。
利用体电流分布的电流元形式计算导轨电流和电枢电流在弹丸中轴线(见图2)上的磁感应强度,并考虑电流在导轨的4个表面的趋肤效应,以及电流在电枢内表面的趋肤效应。设P点为弹丸中轴线上的点,其坐标为(0,0,zP).
1.1 弹丸内膛磁场计算
1.1.1 电枢电流产生的磁场
设电枢电流元的源点位于(x,y,z)处,其中z=z(t),则由毕奥- 萨伐尔定律可得
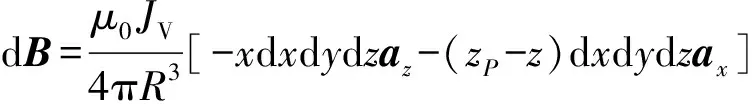
(1)
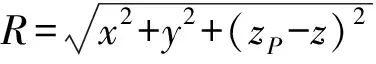
(2)
式中:
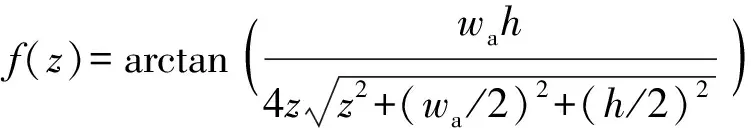
(3)
1.1.2 导轨电流产生的磁场
设上导轨电流元的源点位于(x,y,z)处,其中z=z(t),则上导轨电流元段在P点处的磁感应强度为
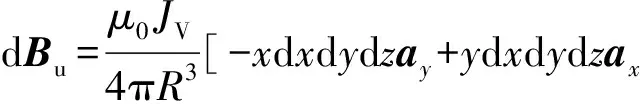
(4)
同理,可得下导轨电流元段在P点处的磁感应强度为
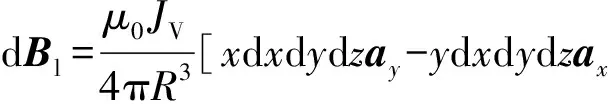
(5)
(4)式、(5)式表明,导轨在z轴方向的磁感应强度为0,同时由于上下导轨均关于x轴对称,则上下导轨电流在y方向的磁感应强度积分和均为0. 又上导轨和下导轨关于Oxz平面对称,因此,在P点处产生的x方向上的磁感应强度相同,则导轨在P点处的磁感应强度为
(6)
式中:
(7)
P点处的磁感应强度为电枢电流和导轨电流磁感应强度的叠加,即
(8)
由(2)式和(6)式可知:By=0,Bz=0,即P点处只有x轴方向的磁感应强度。在计算电枢和导轨产生的磁感应强度时,随着弹丸的运动,电枢电流元的源点坐标zP发生变化,同时电流流过导轨的长度z(t)也发生变化,且与电枢和导轨上的电流趋肤深度有关。因此,需要分析弹丸在输入电流作用下的运动特性以及电流趋肤深度的变化规律。
1.2 弹丸内弹道运动计算
由于对称关系,电枢只受到导轨方向的电磁力,即z轴方向的受力。弹丸在输入电流I的作用下,所受安培力为
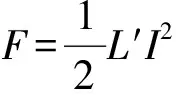
(9)
式中:L′表示导轨的电感梯度(μH /m)。
实际电磁炮发射过程中,一体化弹丸除受到电磁力外,还会受到空气阻力、电枢与炮膛间的摩擦阻力等外力的作用。这些因素的客观存在,对弹丸的速度和位移会产生较大的影响。下面对这些阻力进行分析。
1)空气阻力。空气阻力与速度有关,还与弹丸的横截面积有关,其近似表达式[12]为
Fa=1.1ρaSv2,
(10)
式中:ρa表示空气密度,在标准状况下,空气密度为1.29 kg/m3;S为炮膛截面积;v为弹丸运动速度。
2)摩擦阻力。一体化弹丸与导轨接触部分包括枢轨接触面以及弹托与导轨的接触面。为简化计算,忽略弹托与导轨的摩擦阻力,则弹丸运动过程中的摩擦阻力计算公式为
Ff=fFN,
(11)
式中:f表示摩擦系数,与导轨和电枢的材料有关;FN为弹丸对上下两根导轨的压力,包括推弹过程中的预紧压力以及弹丸运动过程中的电磁扩张力。
因此,弹丸受到的合力为
Fz=F-Fa-Ff,
(12)
则t时刻的弹丸运动速度为
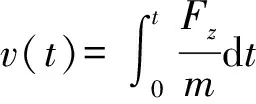
(13)
t时刻的弹丸位移为
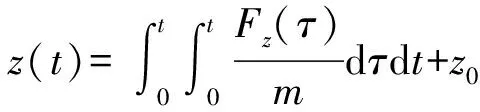
(14)
式中:m为弹丸质量;z0为弹丸初始位移。
2 发射试验和仿真
针对上述弹丸内膛的磁场分布特性和内弹道的动力学特性分析,采用实验室设计的脉冲功率电源放电电流作为导轨的激励电流。导轨材料为黄铜合金,电导率为5×107S/m,电枢材料为铝,电导率为2.46×107S/m. 电磁发射装置的等效电路如图3所示,其中电路各参数为电容C=0.26 F,电感L=2.5 μH,电阻R=0.01 Ω. 得到的电流波形如图4所示,峰值电流约为300 kA.
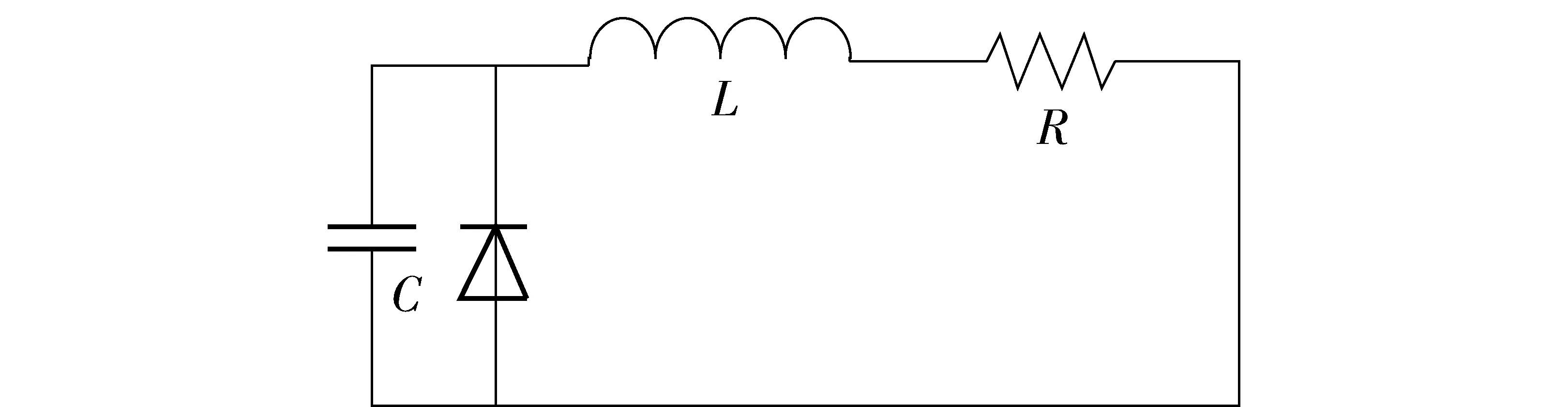
图3 电磁发射装置等效电路图Fig.3 Equivalent circuit of electromagnetic launcher
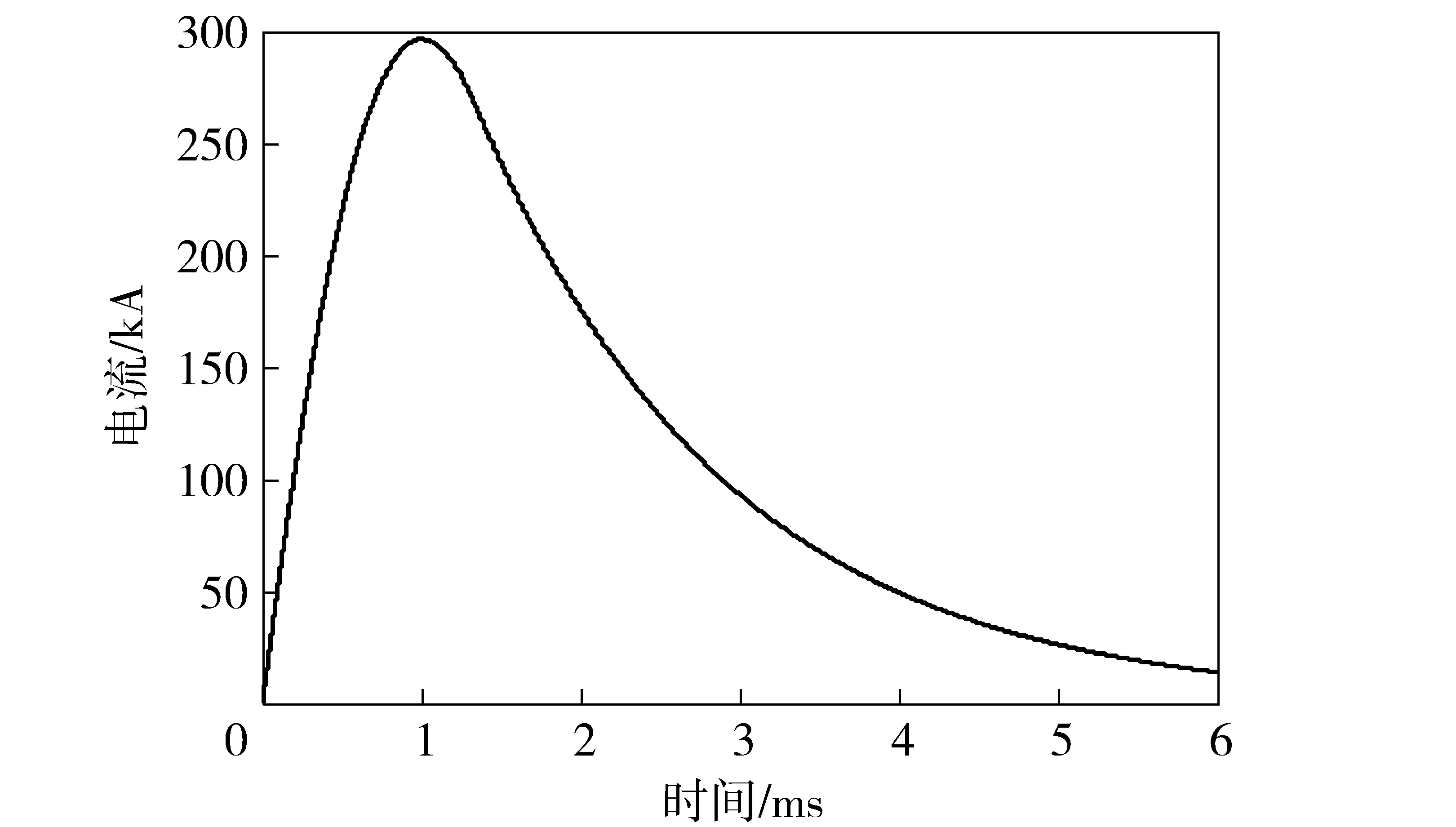
图4 脉冲功率电源放电电流波形Fig.4 Current waveform of pulsed power supply
2.1 电流趋肤深度仿真
假定流经导轨和电枢上的电流在趋肤深度内均匀分布,导轨电流趋肤深度可根据(15)式得到近似结果[11]。
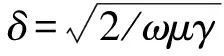
(15)
式中:ω表示电流频率;μ、γ分别表示导体的磁导率和电导率。由于加载在导轨上的电流是瞬态信号(见图4),因此电流趋肤深度随时间发生变化。采用时频分析方法[12]得到电流信号瞬时频率估计曲线(图5中蓝色曲线)。以计算导轨上电流趋肤深度为例,将电流瞬时频率代入 (15)式,同时考虑到电流趋肤深度不大于1/2导轨厚度,因此,电流趋肤深度随时间的变化曲线如图5绿色曲线所示。
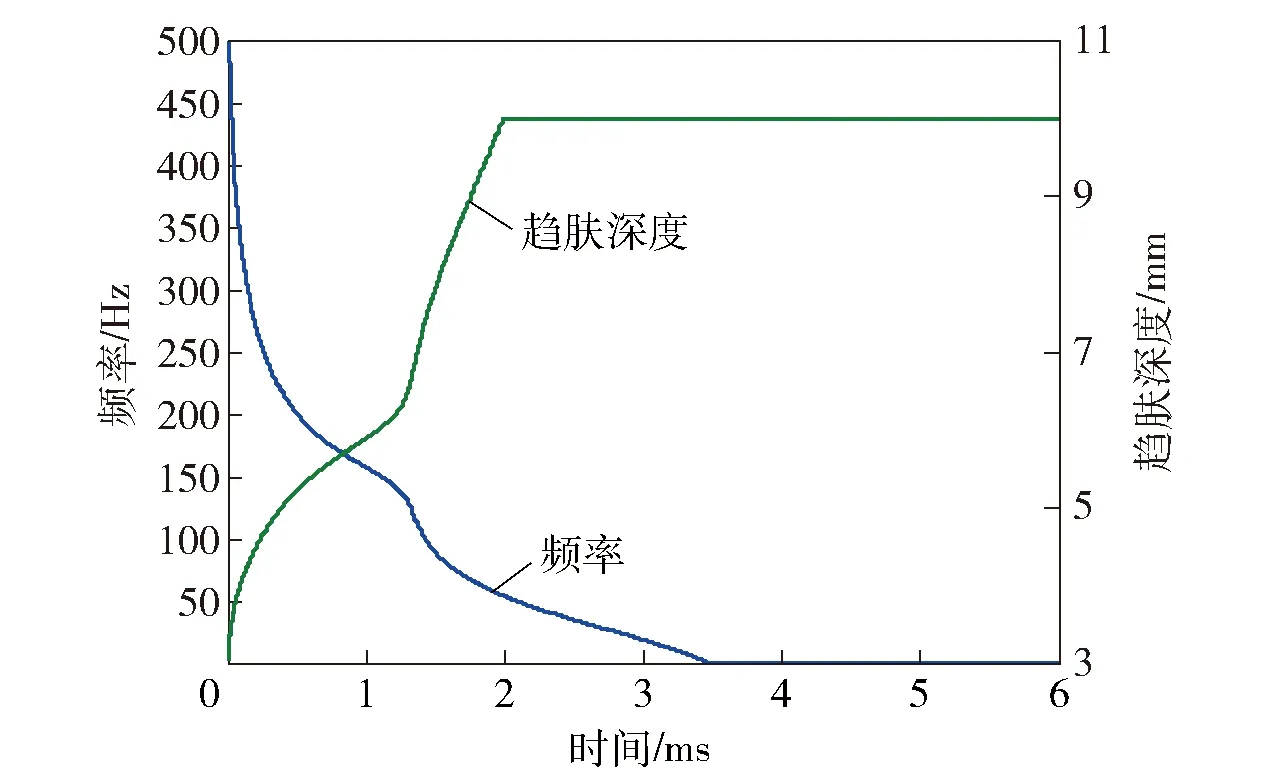
图5 电流瞬时频率及趋肤深度变化曲线Fig.5 Current instantaneous frequency vs. current skin depth
从图5可看出,随着时间的推移,电流频率逐渐下降,在初始阶段,电流工作频率约450 Hz,在出炮口时只有几赫兹。电流频率下降,导致电流趋肤深度逐渐变大。
2.2 导轨电感梯度仿真
在导轨尺寸一定的情况下,导轨电感梯度与输入电流的频率有关,采用时谐分析方法,在导轨端面施加不同频率的激励电流,可得到电感梯度随输入电流频率的变化曲线[12],如图6所示。
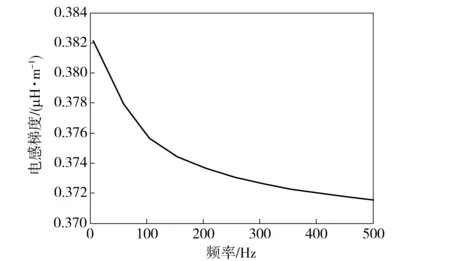
图6 电感梯度随电流频率变化曲线Fig.6 Inductance gradient vs. current frequency
从图6可看出,电流频率越大,电流趋肤深度越小,电枢受到的电磁力越小,由(9)式可知导轨的电感梯度越大。
上述电感梯度随频率的变化关系是基于电枢静止情况下的仿真结果。实际上,电枢在不同的位置,输入同样大小的激励电流,所得到的电流分布及电枢受力都不一样,造成所求得的导轨电感梯度有所差异。采用时谐分析方法[12],并利用Ansoft参数化扫描方法,分析电枢在不同位置时电感梯度的变化规律,如表1所示。
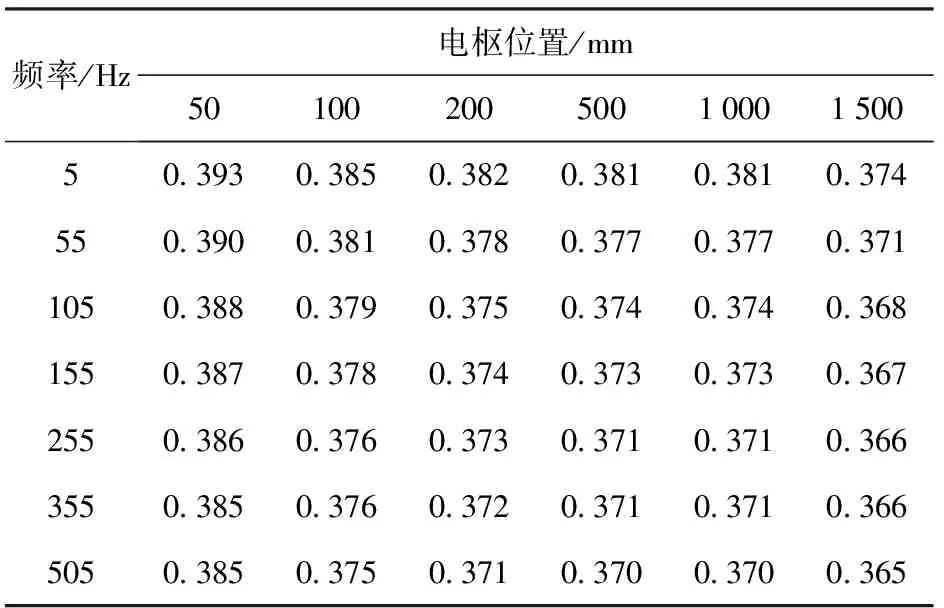
表1 电感梯度随电枢位置和电流频率变化情况Tab.1 Variation of inductance gradient with armature location and current frequency μH/m
由表1可知,电枢越远离炮尾,电感梯度越小,其变化规律越来越平缓。分析原因,在激励电流不变时,电枢离炮尾越远,导轨耗能和储能均增加,根据能量守恒定理,电枢的动能越小。因此,电枢所受电磁力越小,由(9)式可知导轨的电感梯度变小。
从上述的分析可知,导轨的电感梯度与电流频率和电枢运动位置都有关系,采用数值拟合的方法得到电感梯度与二者之间的函数关系式为
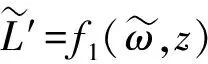
(16)
2.3 弹丸内弹道动力学仿真
将由(16)式得到的电感梯度的拟合公式代入(9)式、(13)式和(14)式,对弹丸在膛内的运动情况进行仿真。仿真参数为:m=67 g,f=0.3,z0=150 mm,可得弹丸的速度曲线和位移,如图7所示。
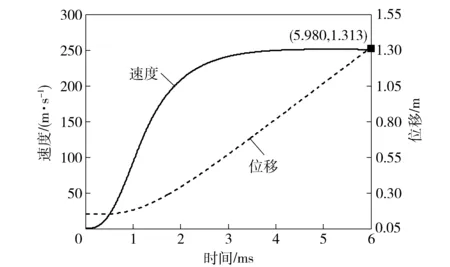
图7 弹丸运动曲线Fig.7 Motion curves of projectile
图7表明弹丸加速度在电流上升阶段越来越大,到电流峰值时达到最大,之后逐渐减小。弹丸出炮口速度达到250 m/s,此时弹丸运动距离为1.3 m.
2.4 弹丸内膛磁场仿真
将(14)式、(15)式和(16)式代入(8)式,可得到在图4所示的输入电流作用下弹丸中轴线最大磁场分布,如图8(a)所示。电枢前端面中心点处的磁场信号振幅谱特性如图8(b)所示。
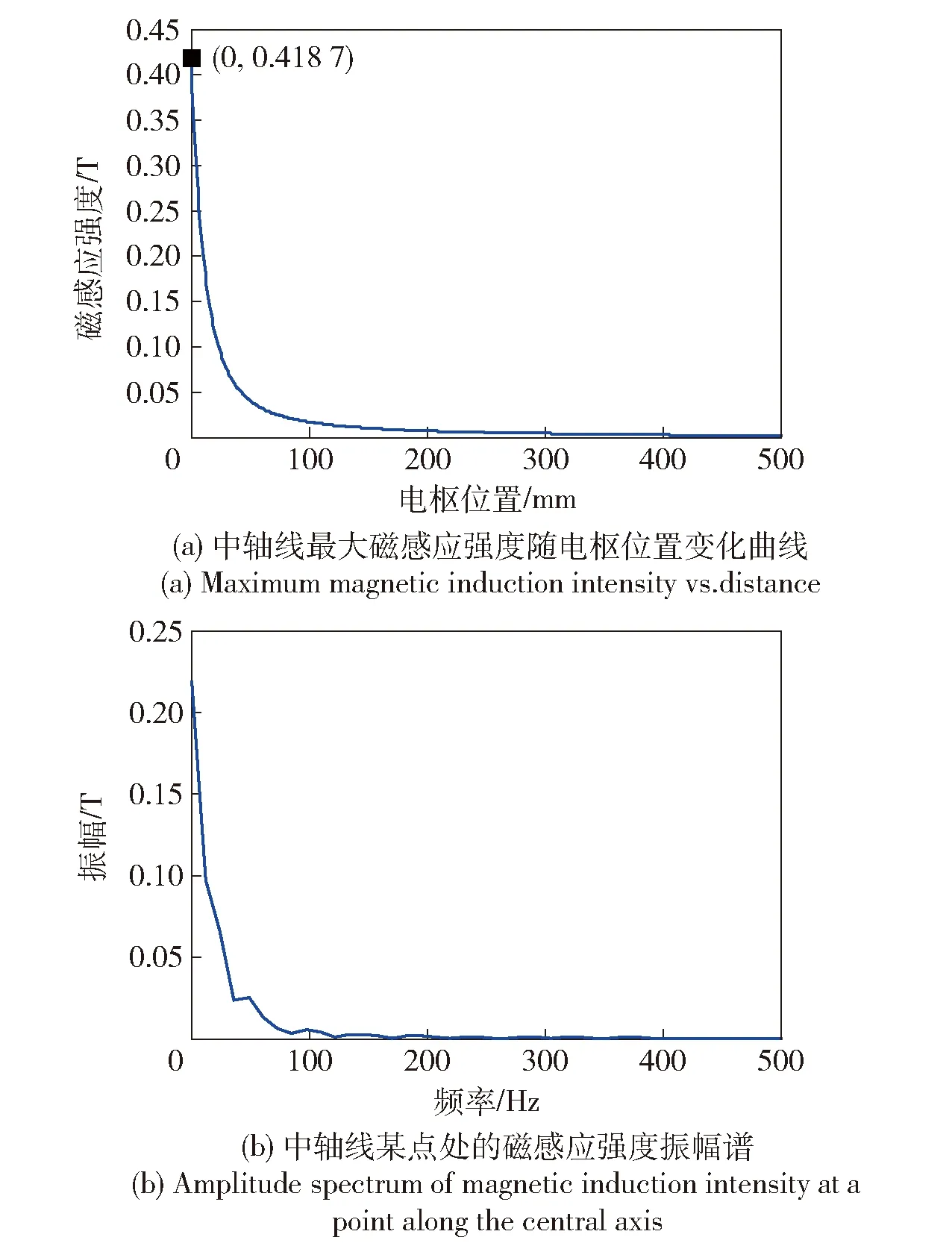
图8 磁场仿真结果Fig.8 Simulated results of electromagnetic field
图8(a)表明,随着离弹丸距离的增加,中轴线磁感应强度逐渐减小,最大磁感应强度为0.4 T,在距离弹丸电枢端面100 mm处,磁感应强度接近0. 图8(b)表明弹丸内部的磁场信号频率主要集中在450 Hz以下的低频段,属于低频强磁场信号,这主要由输入电流信号频率决定。
2.5 试验验证
对时变磁场的测量,一般采用感应线圈[13]。在M点处放置一个磁探针(感应线圈的一种),线圈面与导轨方向即z轴垂直,M点在图2所示坐标系下的坐标为(d,0,zM),d为x方向距离,通过理论计算模型计算通过该点线圈上的感应电压。由于导轨电流不会产生沿z方向的磁感应强度,因此只有电枢上的电流会在M点产生z方向的磁感应强度,则有
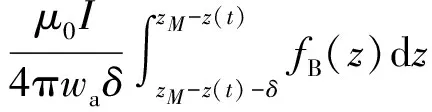
(17)
式中:
fB(z)=g(z,d+wa/2,h/2)-g(z,d-wa/2,h/2).
(18)
若线圈半径足够小,则忽略线圈上每一点磁感应强度的差异性,由法拉第磁感应定律可得线圈上感应电压计算公式为

(19)
式中:Φ为磁通;N表示线圈匝数;A表示线圈面积。用(19)式计算的线圈感应电压同采用磁探针测量的试验结果进行对比,线圈半径为2 mm,匝数为5,中心坐标为(35 mm,0 mm,1 240 mm),验证理论计算模型的正确性,对比结果如图9所示。
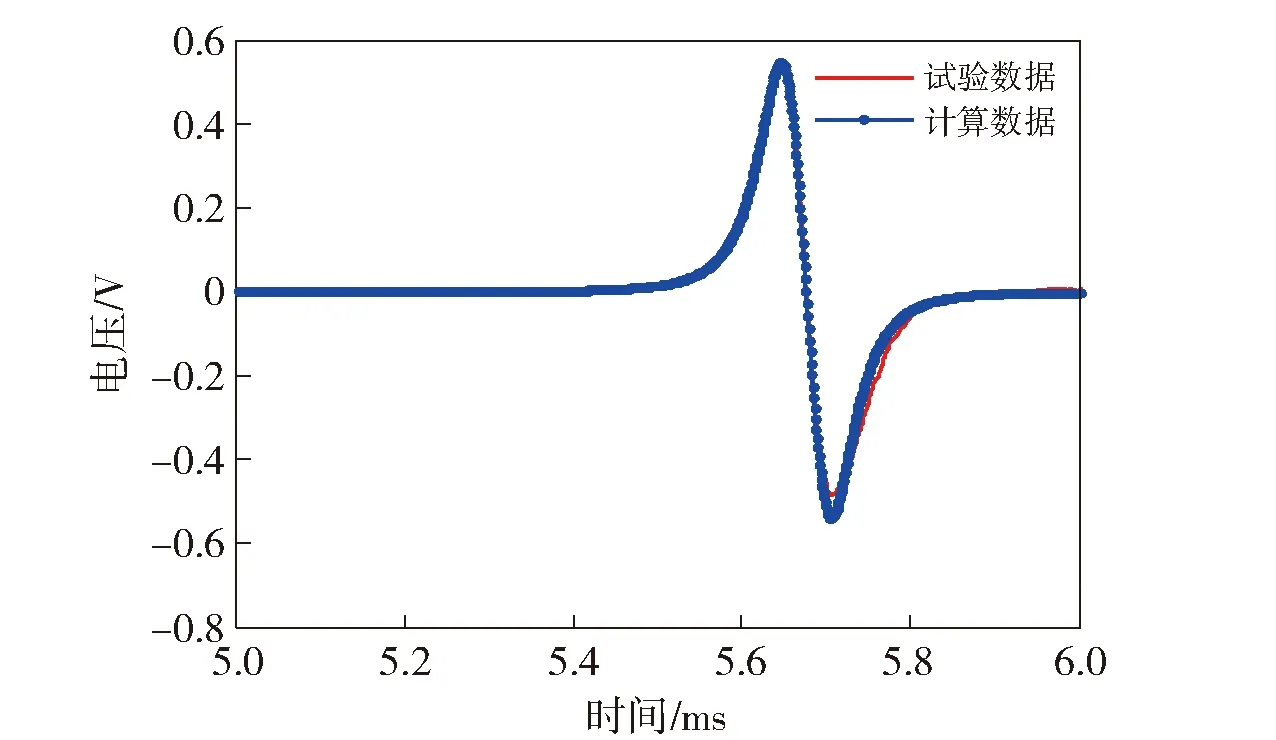
图9 磁探针测量数据与计算仿真数据对比Fig.9 Comparison of measured data of magnetic probe and simulated data
图9表明,采用理论计算模型计算的磁探针的感应电压与试验测量的数据比较接近。存在偏差的原因是:一方面, 本文的模型没有考虑速度趋肤对电流分布的影响;另一方面, 由于试验过程中磁探针受导轨震动的影响,导致位置会有所偏差。因此,造成一定的试验误差。所采用的理论计算模型对电磁发射装置膛内的磁场分布特性分析精度较高。
3 结论
一体化制导弹丸在电磁发射装置膛内的发射过程中,强磁场对弹丸内部的电子元器件布局有较大的影响。本文基于毕奥- 萨伐尔定律,采用体电流分布的电流元形式,同时考虑弹丸运动位移和电流趋肤深度对磁感应强度的影响,并结合时谐分析方法和时频分析方法建立了弹丸中轴线上磁感应强度的理论计算模型,对弹丸中轴线的磁感应强度进行了解析计算。采用时频分析方法对激励电流信号进行瞬时频率估计,得到电流瞬时频率随时间的变化曲线,继而得到电流趋肤深度的变化曲线。动态仿真了弹丸中轴线上的瞬态电磁场分布情况,最后利用磁探针的试验数据验证了模型的准确性。仿真结果表明:弹丸中轴线的磁感应强度沿弹丸长度方向迅速衰减,到离电枢端面100 mm处基本为0. 本文计算仿真了一体化弹丸中轴线的磁场分布特性,对制导弹丸内部电子器件的布局具有一定的指导作用。
References)
[1] Fair H D. Electric launch science and technology in the United States[J]. IEEE Transactions on Magnetics, 2003, 39(1): 11-17.
[2] Reed J D. Keynote remarks at the 12th symposium on electromagnetic launch technology[J]. IEEE Transactions on Magnetics, 2005, 41(1): 155-157.
[3] Pencil E J, Kamhawi H, Gilland J H, et al. Overview of advanced electromagnetic propulsion development at NASN Glenn Research Center, NASA/TM-2005-213888[R]. Washington: the NASA Program Office, 2005.
[4] 高成,刘晓,石立化, 等. 低频强磁场屏蔽效能的测试方法与测试设备研制[J]. 高电压技术,2010,36(9):2272-2277. GAO Cheng, LIU Xiao, SHI Li-hua, et al. Measurement method and measurement equipment development for low-frequency magnetic field[J].High Voltage Engineering, 2010, 36(9): 2272-2277.(in Chinese)
[5] 杨玉东,付成芳,薛文, 等.轨道与弹丸间运动电磁场分布的数值计算[J]. 火炮发射与控制学报,2014,35(3): 1-5. YANG Yu-dong, FU Cheng-fang, XUE Wen, et al. Numerical calculation of movement electromagnetic field distribution between rail and armature[J]. Journal of Gun Launch & Control, 2014, 35(3): 1-5. (in Chinese)
[6] 周媛,严萍,袁伟群, 等.电磁轨道发射装置中导轨几何参数对电感梯度的影响[J].电工电能新技术,2009, 28(3): 23-27. ZHOU Yuan, YAN Ping, YUAN Wei-qun, et al. Effect of rail geometrical parameters on inductance gradient of EML[J]. Advanced Technology of Electrical Engineering and Energy, 2009, 28(3): 23-27. (in Chinese)
[7] Nie J X, Han J J, Jia Q J, et al. An analytic expression of induction gradient for rail-type electromagnetic launcher [J]. IEEE Transactions on Plasma Science, 2011, 39(3): 931-934.
[8] 李迎生. 小口径电磁轨道炮内弹道特性初步研究[D].南京:南京理工大学,2007. LI Ying-sheng. Primary study on interior ballistics of a small caliber electromagnetically railgun[D]. Nanjing: Nanjing University of Science and Technology, 2007. (in Chinese)
[9] Geng Y B, Xu L Z. Analysis of projectile motion in bore and transfer efficiency for electromagnetic railgun[C]∥2010 WASE International Conference on Information Engineering (ICIE). Beidaihe, China: IEEE, 2010: 156-160.
[10] Kong H T, Ji L C, Yuan W Q, et al. Research on interior ballistic mechanics of electromagnetic Railgun [C]∥2012 16th International Symposium on Electromagnetic Launch Technology (EML). Beijing, China: IEEE, 2012.
[11] Marshall R A, Wang Y. Railguns: their science and technology[M]. Beijing: China Machine Press, 2004: 1-10.
[12] 杨玉东,王建新,薛文. 轨道炮动态负载特性的分析与仿真[J].兵工学报,2010, 31(8): 1026-1031. YANG Yu-dong, WANG Jian-xin, XUE Wen. Simulation and analysis for dynamic load characteristic of railgun[J]. Acta Armamentarii, 2010, 31(8): 1026-1031. (in Chinese)
[13] 潘启军,马伟明,赵治华, 等. 磁场测量方法的发展及应用[J]. 电工技术学报, 2005, 20(3): 7-13. PAN Qi-jun, MA Wei-ming, ZHAO Zhi-hua, et al. Development and application of measurement method for magnetic field[J]. Transactions of China Electrotechnical Society, 2005, 20(3): 7-13. (in Chinese)
Analysis of Distribution Characteristics of In-bore Magnetic Field of Electromagnetically Launched Projectile Based on Analytical Method
LI Xiang-ping, LU Jun-yong, LI Yu, WU Xiao-kang
(National Key Laboratory for Vessel Integrated Power System Technology, Naval University of Engineering,Wuhan 430033, Hubei, China)
The in-bore magnetic field distribution characteristics of electromagnetic launcher should be considered in the layout design of components in guided projectile. The high in-bore magnetic field generated by electromagnetic launcher is analyzed, and a formula for magnetic field distribution is deduced based on Biot-Savart law, in which projectile displacement and current skin depth are considered. The relationship between inductance gradient, current frequency and projectile’s location is obtained by time-harmonic analysis and data fitting to analyze the in-bore kinetic characteristics of projectile interior trajectory. And the time-frequency analysis method is used to achieve the relationship between current skin depth and time to build a 3-D theoretical calculation model (TCM) for the distribution characteristics of magnetic field along the central axis of projectile. A laboratory electromagnetic launcher is taken for example, and the experimental data is used as input for simulation. The results show that the in-bore magnetic induction intensity frequency is below 450 Hz and the peak of in-bore magnetic induction intensity is up to 0.4 T, which gets weaker along the length direction of projectile and approximates to 0 at 100 mm. The validity of TCM is verified by using the experimental data of magnetic probe.
ordnance science and technology; electromagnetic launch; in-bore magnetic field analysis; Biot-Savart law; current skin effect; time-harmonic analysis; time-frequency analysis
2016-05-10
国家自然科学基金项目(51407191、51307176);国家“973”计划项目(6132620102)
李湘平(1990—),男,博士研究生。E-mail:511422906@qq.com; 鲁军勇(1978—),男,研究员,博士生导师。E-mail:jylu@xinhuanet.com
10.3969/j.issn.1000-1093.2016.12.004
TM153+.1; TJ012.1+5
A
1000-1093(2016)12-2205-07

