地震作用下高边坡破坏的振动台试验

闫坤伐, 卢建华，刘晓燕, 周志军

(1.长安大学 特殊地区公路工程教育部重点试验室,陕西 西安 7100643；2.陕西省审计厅，陕西 西安 710002)

地震作用下高边坡破坏的振动台试验

闫坤伐1, 卢建华2，刘晓燕1, 周志军1

(1.长安大学 特殊地区公路工程教育部重点试验室,陕西 西安 7100643；2.陕西省审计厅，陕西 西安 710002)

通过振动台模型试验，探讨含软弱夹层结构面、不同坡面形态的高边坡破坏特征及破坏机理，分析地质条件、地震荷载对边坡破坏变形的影响。试验结果表明：含泥化软弱夹层处易产生崩塌、滑移等失稳破坏现象。其中凹坡破坏以坡肩崩塌、变坡线上部整体滑移为主，破坏模式主要为坡顶形成的拉裂缝带动坡肩滑出坡体的影响；凸坡破坏以变坡线附近崩塌为主，破坏模式主要为变坡线处拉裂缝带动变坡线分层界面出现剪出崩塌；凹坡较凸坡不稳定，振动强度越大边坡变形破坏越显著；频率越接近模型的自振频率，边坡破坏越严重；持时与地震动输入的总能量密切相关。

高边坡；坡面形态；振动台试验；动力破坏；地震荷载

边坡在动力荷载作用下的破坏变形主要为累积效应和诱发失稳，而边坡失稳破坏类型以滑坡和崩塌为主[1]。对于岩质边坡破坏方式，可从岩体结构类型入手分析，其滑动面和分离面往往是岩体软弱夹层等结构面。当层面、断层等不连续面倾角小于坡面倾角时，可形成平面型破坏；当存在2个不连续面与坡面倾向一致时，可形成双平面型破坏；2个不连续面的交叉可形成楔体型破坏；坡体内若有几组节理裂缝，其中一组走向与坡面相同，但小于坡面倾角，另一组反倾走向，可产生阶梯型破坏；由反倾走向或顺倾陡坡，能形成倾倒型破坏；多组节理裂缝构成滑移面的边坡、岩石强度较低的岩质边坡易形成圆弧型破坏。岩质高边坡受到自身重力作用，错综复杂的节理裂缝等构成滑动面，使部分不连续面被切断，形成复合型破坏。国内外学者对地震荷载作用下边坡的变形破坏特征及机理做大量的研究工作[2-4]，并取得一定的成果。周飞等[5]利用振动台模型和正交试验研究了斜坡的加速度响应特征及影响因素。仅考虑含有软弱夹层简单坡的变形破坏。侯红娟等[6-7]在强震作用下均质斜坡大型振动台试验研究的基础上，进行水平层状结构斜坡地震动力响应的振动台试验研究。该模型是一个简化的斜坡模型，没考虑斜坡形态、岩性组合等的影响。叶海林等[8-9]采用振动台模拟试验，通过输入较大的地震波使边坡破坏，并用数值分析加以验证试验结论的合理性，证明振动台模型试验结果的合理性及数值分析方法的可靠性。该试验仅对凹坡进行分析坡型比较单一。林杭等[10-11]采用数值模拟软件研究层状岩质边坡的破坏特征，通过强度折减法分析结构面倾角与稳定性的关系。黄昕等[12]进行了室内模型试验并采用Sama法对层状块裂岩体边坡的变形破坏和稳定性开展研究。模型设计仅考虑不同开挖坡度与层理倾角。范刚等[13]利用振动台试验，研究含泥化夹层顺层岩质边坡的破坏模式：拉裂-滑移-崩落式。该试验需进一步考虑不同坡面形态的高边坡破坏。本文结合已有理论和试验研究成果，开展不同坡面形态岩质高边坡为研究对象的大型振动台模型试验。试验设计了含有多层软弱夹层结构面的岩质边坡，在模型箱中并列放置，通过加载不同地震动参数的工况，研究地震荷载作用下模型边坡破坏特征。

1 模型试验

1.1 振动台参数

试验采用西安建筑科技大学结构工程与抗震教育部重点试验室2.2 m×2 m单向双自由度振动台，最大试件重量为40 kN，最大加速度±27.7 m/s2。最大振幅±100 mm。工作频率范围0.01～30 Hz。

1.2 模型试验相似关系

本文基于π定理用量纲分析法导出相似判据。因模型的复杂性，很难满足所有参数相似性，需根据试验目的和模型特性选择主控参数，作为基本量纲进行分析。本试验以几何长度，密度和加速度为基本量纲，推导得出振动台模型试验相似常数见表1。

表1 模型试验相似常数(带*号为基本量纲)Table 1 Similarity codfficients of model test

1.3 模型设计

试验采用刚性模型箱外部尺寸长宽高为1.94 m×1.3 m×1.1 m。便于观察振动过程中破坏现象，模型箱两侧采用有机玻璃，并在模型箱后壁加衬5 cm厚泡沫垫层从而减小模型箱边界效应。中间采用木挡板使2个模型分开，挡板采用防水光滑木质材料且挡板与箱体用角钢和螺栓固定。模型各参数为：凸、凹坡尺寸1.2 m×0.65 m×1 m；均采用1∶0.5和1∶1 2个坡率；坡顶宽0.4 m；坡体内设4层泥化夹层界面，距箱底分别为0.2，0.5，0.7和0.9 m；坡脚台阶高为0.15 m，为增加模型稳定性台阶铺满整个模型箱并压实。试验分别采用加速度传感器和位移传感器，考虑试验条件及避免破坏模型完整性等因素，本次共布设18个加速度传感器和4个位移传感器。布置详图见图1。

1.4 材料选取

根据相似原理，设计选用的材料模型与原型密度相同，通过直剪、三轴试验确定材料参数，试验模型的配合比为重晶石粉∶石英砂∶石膏粉∶水按照32∶56∶9∶8的配比制作边坡模型[14-15]。试验证明，该配合比能满足模型与原型之间的相似比例，可较好满足各项物理力学参数指标。表2为泥岩及相似材料的主要物理力学参数指标。

1.5 试验加载方案

本试验旨在研究地震波振动强度、频率、类型等对岩质边坡的动力响应规律，因此采用了时间压缩比为5.48的ELC波和SIN波。具体试验加载方案见表3。

单位: m(a)凹型;(b)凸型图1 模型边坡示意图Fig.1 Schematicdiagram of model slope

表2 原型和模型的主要物理力学参数表Table 2 Physical and mechanical parameter table of Prototype and the model

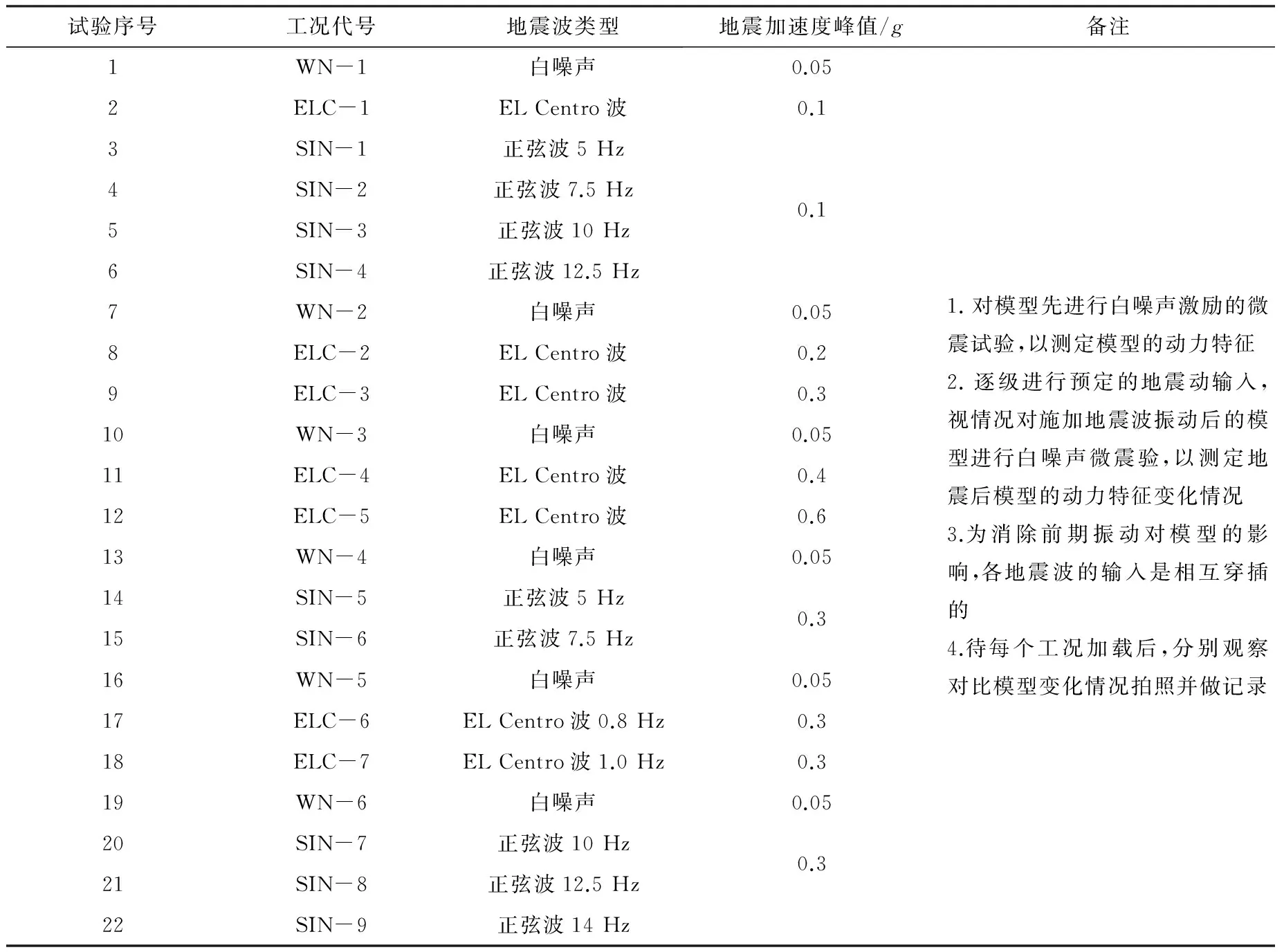
表3 模型边坡加载制度Table 3 Load rules of the model slope

2 模型边坡变形破坏现象

2.1 凸坡变形破坏现象

试验前期由于各地震动参数不足以产生边坡变形，致使观测到的模型变形破坏无明显现象。加载到SIN-6时，坡肩上部出现裂缝，从坡体边缘向坡体内部扩展延伸，含软弱夹层的分层界面处均产生裂缝。边坡受地震力作用表现出高程效应及存在水平软弱结构面其变形破坏往往从这些薄弱部位开始，ELC-6也证实这一现象，第3个夹层界面产生2条细小裂缝，垂直于夹层界面，并向变坡线处延伸，第2个夹层界面侧面延伸出一条长度8 cm左右的斜交裂缝。观测SIN-8得出凸坡变坡线附近、2个泥化分层界面中间部分，受到较强烈的地震荷载后首先出现局部崩塌现象。从一侧有机玻璃观察发现，坡体内部产生多条垂直于结构面发育的张拉裂缝，最外侧靠近坡面的一条裂缝弯曲向坡面方向发展。见图2。

试验过程中观测到的宏观现象，虽可全面反应出边坡变形破坏过程，但对于坡内变形破坏只能通过有机玻璃一侧进行观测，为更全面了解坡内裂缝走向和分布状况，试验完成后对已破坏的模型边坡进行开挖，即先挖除模型的一半，观察记录坡体内部裂缝的大体走向分布规律。图3(a)和3(b)为模型开挖过程中观测的现象，可看出凸坡变坡线附近的位置有几条宽裂缝，呈弧形分布，直接贯通至变坡线下部。

图2 模型边坡的破坏照片Fig.2 Failure photos of slope model

图3 边坡开挖中的现象Fig.3 Phenomenon of slope excavation

2.2 凹坡变形破坏现象

试验前期模型同样无明显现象。加载到SIN-6坡肩左右两侧均出现裂缝，ELC-6和ELC-7泥化夹层界面产生错动，且上部岩体在地震荷载作用下有沿泥化界面向临空面剪出现象，坡脚受上部模型挤压产生堆积凸起面，最终整个坡体失稳破坏。整个模型变形破坏是一个循序渐进的过程，从裂缝产生到裂缝延伸扩展，再到潜在滑移面形成，至最终滑移面错动出现坡体崩塌。SIN-8可观测凹坡变形破坏的最终状态。见图2。凹坡崩塌主发生在含软弱夹层的分层界面处和地形较突出、陡缓交接的转折变坡线部位。这主要与边坡输入地震波的放大效应和边坡的临空条件有关系。

同样对凹坡进行开挖分析，图3(c)和3(d)为模型开挖过程观测到的现象：凹坡内部裂缝纵横交错，但有一条较宽裂缝从坡顶一直延伸至坡肩位置，和软弱夹层贯通，可见该裂缝为坡肩崩塌的主裂缝。

3 高边坡变形破坏影响因素分析

影响高边坡变形破坏的因素很多，除了岩土体结构和岩性组合特征、地形地貌、高程、坡率及坡体含有软弱夹层等地质条件外，还与地震波类型和地震波振动强度、频率、方向等参数密切相关。本试验主要从边坡坡面形态、结构面特征、高程以及地震荷载条件等因素展开分析。

3.1 地质条件影响

3.1.1 坡面形态的影响

以输入加速度值0.3g的ELC波为例，从图4可以得出：凸、凹坡对称测点的PGA放大系数整体相差不大，但凹坡测点PGA放大系数要略大于对应的凸坡。对比2种坡面形态有如下特点：两坡面形态PGA放大系数均沿高程整体呈放大趋势，在变坡线以下(即大致1/2高程处)两者数值上相差不大；两坡型PGA放大系数均在变坡线附近出现急剧增大趋势，变坡线下一测点(高程40 cm)增幅尤为剧烈，同时变坡线上又出现局部减小的现象；两坡型PGA放大系数均在坡肩处再次出现急剧增大趋势，数值上明显高于其他测点。凹坡各测点PGA放大系数整体上略大于凸坡，变坡线以上这一特点更为显著。通过PGA放大系数沿高程方向构成的曲线可得出，凸、凹坡均以折线形式变化，而凹坡PGA放大系数构成的折线更为复杂；主要是由于在变坡线附近出现坡率变化，这一位置处加速度放大效应尤为显著，使得附近测点PGA放大系数陡增。凹坡相对于凸坡在坡肩处(高80 cm)PGA放大效应更加明显。

图4 0.3g EL C波2种坡面形态下各测点PGA放大系数Fig.4 0.3g EL C wave in two of slope form each measuring PGA amplification coefficient

结合边坡破坏现象知：随地震波的输入，凹、凸坡呈现出不同破坏模式。凹坡在变坡线上部出现明显的崩塌，坡顶出现贯通大裂缝，坡脚出现堆积凸起面。凸坡在变坡线附近有崩塌现象发生，坡顶和坡体内部出现裂缝，整体稳定性明显强于凹坡。在地震荷载作用下，凹坡较凸坡的加速度动力反应更敏感，更不稳定。造成稳定差异的原因可能是凹坡在坡面斜率突变的地方出现剪应变集中区和地震力的作用下边坡表面岩土体产生破坏，导致动荷载传递异常。

3.1.2 坡体结构的影响

由试验工况可知，夹层界面处软弱夹层把坡体分成多个部分，在夹层界面之间的坡体更易产生错动滑移，直至整体滑出崩塌。软弱夹层降低了坡体的整体稳定性，是边坡变形破坏的触发点，对诱发边坡破坏有很大的影响。设计的4组泥化分层界面均出现不同程度滑移，变坡线上部较下部错动滑移更加明显。这一方面说明高程放大效应显著；另一方面也说明软弱夹层等结构面是边坡的薄弱环节，这些区域受到地震荷载作用，常会诱发边坡的整体失稳破坏。因此，坡体结构特征控制着边坡的失稳破坏模式，当边坡没有控制性结构面时其破坏模式主要受坡角，坡面形态，边坡岩性组合的影响；有明显控制性结构面的边坡，其变形破坏往往取决于结构面产状及其与水平地震力作用方向，斜坡坡面产状的组合情况。

3.2 地震荷载条件影响

3.2.1 地震波类型的影响

在不同加速度条件下,设计ELC波和SIN波2种地震波，以ELC-1和SIN-1为例，见图5。分析凸坡坡面测点A4，A6和A12,发现SIN-1工况各测点PGA放大系数明显大于相应ELC-1工况，得出不同的地震波作用下加速度放大效应不同，原因可能是不同的地震波其频谱特性差异很大。

图5 凸坡坡面PGA放大系数与地震波的关系Fig.5 Relationship between PGA amplification factor and seismic wave in convex slope

加速度幅值较小时破坏现象不明显。随幅值增加，边坡模型的动力响应强烈，产生裂缝和滑移。加速度幅值的持续加大，裂缝不断延伸和扩展直至模型破坏。原因：边坡上地震波振动强度越大，其产生的地震惯性力就越大，对边坡的破坏性就会越大。在地震动参数相同的情况下，正弦波对边坡模型的破坏力明显要强于ELC波。

3.2.2 频率的影响

以加速度幅值0.1g不同频率SIN波的加载方案得到不同高程测点PGA放大系数：图6凸坡坡内A9和A14测点PGA放大系数随地震频率的增加表现增大趋势，A3测点先保持平稳后急剧增大；坡表A4和A12测点PGA放大系数持续缓慢增大，后期增加幅度较大，A6和A10测点PGA放大系数随频率增大表现先急后缓，整体依然表现为增大趋势。图7凹坡坡内不同高程测点PGA放大系数随地震频率的增加整体上表现增大趋势；坡表A2和A11测点PGA放大系数持续缓慢增大，A5和A8测点PGA放大系数随频率增大表现出折线递增趋势，但频率为10 Hz左右出现小幅减小，之后随频率增大又继续增加。

结合试验现象知，其他地震动参数相同条件下，在一定范围内频率越大，模型边坡响应越强烈。当频率增加到10 Hz时，边坡动力响应有降低趋势。由此可见，地震波频率接近模型自振频率，边坡模型的破坏更加严重，地震动频率逐渐远离模型自振频率时，土体动力响应减弱。原因：当地震波频率接近模型自振频率时，加速度响应值增大。

(a)坡内；(b)坡表图6 凸坡PGA放大系数与频率的关系Fig.6 Relationship between PGA amplification coefficient and frequency of convex slope

(a)坡内；(b)坡表图7 凹坡PGA放大系数与频率的关系Fig.7 Relationship between PGA amplification coefficient and frequency of concave slope

3.2.3 持续时间的影响

其他条件相同的情况下，加速度较小时，持时对模型的影响不明显。加速度增大一定范围时，持时越长模型动力响应越明显，边坡的变形破坏越剧烈，破坏现象越明显。可见持时与地震动输入的总能量密切相关，地震动总能量导致坡体变形破坏十分关键。原因：地震动对坡体的破坏逐渐累加作用，当地震动持时增加，坡体输入的地震动总能量也在增加，进而导致坡体损伤不断累积，持续作用下边坡变形越严重，产生的位移量继续累积，最终导致坡体失稳破坏。

3.2.4 振动强度的影响

试验设计了不同加速度幅值2种地震波的输入方案，ELC波加速度幅值为0.1，0.2，0.3，0.4，0.6和0.8g等6个等级，SIN波加速度幅值为0.1g和0.3g。

图8和图9可知在小幅值(0.1～0.3g左右)PGA放大系数呈增大趋势，个别测点有小幅波动；幅值在0.4～0.6g间基本保持稳定，幅值超过0.6g后又出现递减趋势。分析：凸坡坡内A3测点在幅值0.1～0.3gPGA放大系数小幅增加，随后急剧减小，且幅度较大； A9和A14测点基本保持先增加再稳定后减小趋势。坡表测点PGA放大系数整体呈现前期小幅波动并保持增大，后期逐渐减小趋势。凹坡坡内测点PGA放大系数在幅值0.1～0.3g逐渐增大，A13测点增幅最大，后期各测点PGA放大系数均逐渐减小，A1测点减小趋势最为显著，减小幅度也较大；坡表各测点同样呈现出上述特点，即0.1～0.3g左右PGA放大系数逐渐增大，之后保持稳定，最后减小。

图8 凸坡PGA放大系数与加速度的关系Fig.8 Relationship between PGA amplification factor and acceleration of convex slope

图9 凹坡PGA放大系数与加速度的关系Fig.9 Relationship between PGA amplification factor and acceleration of concave slope

分析得出:随地震动幅值增大，测点PGA放大系数大致呈现先增大再稳定后减小的趋势。原因可能为台面输入的加速度幅值越大，动应力水平就会越高，从而剪切模量就会越低，阻尼比增大，边坡土体的隔震减震作用就会越强。董金玉在地震作用下顺层岩质边坡动力响应和破坏模式大型振动台试验研究中得出相同的结论。

4 高边坡变形破坏机理分析

对比分析知：两模型均在坡顶、分层界面及变坡线位置变形破坏显著，地震荷载作用下破坏过程可分为坡顶拉裂缝产生，泥化夹层界面发生水平错动，变坡线处有拉裂缝产生；裂缝及错动进一步扩展延伸，模型上部产生水平滑移；坡顶拉裂缝贯通并在裂缝处向前滑移，变坡线处两分层界面出现剪出崩塌现象，模型完全失稳破坏。由于试验条件等因素限制，为更好描述边坡变形破坏的现象，用图10～11凹、凸坡滑移破坏侧视简图进行分析。图10中虚线为凹坡最终形成的滑移面，各泥化夹层界面及变坡线均为凹坡的薄弱面，最终在这些位置发生破坏。边坡整体发生沉降，变坡线以上的坡肩部分发生崩塌。图11虚线部分边坡变形破坏最为显著，且在变坡线附近发生小范围的崩塌，坡体沿水平软弱夹层发生错动滑移，边坡最终崩塌彻底破坏。

图10 凹坡滑移破坏侧视简图Fig.10 Concave side of the slope sliding failure

图11 凸坡滑移破坏侧视简图Fig.11 Convex side of slope sliding failure

图12为凹、凸坡在地震荷载作用下，边坡变形破坏的过程简图。边坡破坏过程为：凹坡坡顶拉裂缝产生，裂缝进一步延伸扩展，裂缝贯通形成滑移

面，坡肩滑出坡体失稳破坏；凸坡变坡线处有拉裂缝产生，裂缝及错动进一步扩展延伸，变坡线处两分层界面之间出现剪出崩塌；模型完全失稳破坏。

图12 2种坡面形态边坡变形破坏过程Fig.12 Deformation and failure process of two kinds of slopes

5 结论

1)凹坡变形破坏以坡肩崩塌、变坡线上部整体滑移为主；凸坡以变坡线附近崩塌为主；凹坡较凸坡不稳定。坡体结构对边坡的变形破坏很重要，软弱夹层为坡体的薄弱部位，降低了边坡坡体的整体稳定性。

2)地震荷载对边坡的变形破坏起决定性的影响：振动强度越大边坡变形破坏越显著；频率的影响和自振频率有关，越接近模型自振频率，边坡破坏越严重；持时与地震动输入的总能量密切相关，地震动能量的不断累积导致边坡损伤不断累积，这是致使坡体失稳破坏的重要因素。

3)地震荷载作用下边坡变形破坏是不断发展的过程，试验模型均在坡肩、泥化夹层界面及变坡线附近破坏显著，其破坏过程为：凹坡坡顶拉裂缝产生，裂缝进一步延伸扩展，裂缝贯通形成滑移面，坡肩滑出坡体发生失稳破坏；凸坡变坡线处拉裂缝产生，裂缝及错动进一步扩展延伸，变坡线处两分层界面出现剪出崩塌,模型发生失稳破坏。

[1] 李果.强震条件下层状岩体斜坡动力失稳机理研究[D].成都：成都理工大学,2012. LI Guo. Failure mechanism of stratiform rock slope under strong earthquake[D]. Chengdu: Chengdu University of Technology, 2012.

[2] Yegian M K, Marciano E A, Ghahraman V G.Seismic risk analysis for earth dams[J]. J of Geotech Engrg,1991,117(1):18-34.

[3] Meei-Ling Lin, Kuo-Lung Wang. Seismic slope behavior in a large-scale shaking table model test[J]，Engineering Geology， 2006, 86(2):118-133.

[4] 何刘，吴光，赵志明. 坡面形态对边坡动力变形破坏影响的模型试验研究[J].岩土力学,2014,35(1): 111-117. HE Liu，WU Guang，ZHAO Zhiming. Model test of influence of slope surface morphology on dynamic deformation failure[J]. Rock and Soil Mechanics, 2014,35(1): 111-117.

[5] 周飞,许强,刘汉香,等. 地震作用下含水平软弱夹层斜坡动力响应特性研究[J]. 岩土力学, 2016, 37(1):133-139. ZHOU Fei,XU Qiang,LIU Hanxiang, et al.An experimental study of dynamic response characteristics of slope with horizontal weak interlayer under earthquake[J].Rock and Soil Mechanics, 2016,37(1):133-139.

[6] 侯红娟.水平层状斜坡地震动响应特性的振动台试验研究[D].成都：成都理工大学,2013. HOU Hongjuan. The seismic dynamic response characteristics of the shaking table test on horizontally layered slope.Institute of Engineering Mechanics[D]. Chengdu: Chengdu University of Technology,2013.

[7] Tsesarsky M, Hatzor Y H, Sitar N. Dynamic displacement of a block on an inclined plane: analytical,experimetal and DDA results[J]. Rock Mechanics and Rock Engineering,2005,38:153-167.

[8] 叶海林,郑颖人,李安洪.边坡动力破坏特征的振动台模型试验与数值分析[J].土木工程学报，2012，45(9):128-135. YE Hailin, ZHENG Yingren, LI Anhong. Shaking table model test and numerical analysis on dynamic failure characteristics of slope[J]. China Civil Engineering Journal,2012,45(9):128-135.

[9] Lin M L, Wang K L．Seismic slope behavior in a large scale shaking table model test[J]．Engineering Geology，2006，86( 2) : 118-133.

[10] 林杭,曹平,李江腾.层状岩质边坡破坏模式及稳定性的数值分析[J].岩土力学, 2010, 31(10): 3300-3304. LIN Hang,CAO Ping,LI Jiangteng. Numerical analysis of failure modes and stability of stratified rock slopes[J]. Rock and Soil Mechanics,2010,31(10): 3300-3304.

[11] Myong Mo Kim, Hon Yim Ko.Centrifugal testing of slope models[J].Tran Res Rec, 1991(2):7-14.

[12] 黄昕,张子新,徐营.块裂层状岩质边坡稳定性研究[J].地下空间与工程学报,2009,5(5):941- 945. HUANG Xin, ZHANG Zixin,XU Ying. Study on the stability of block-layered rock slope[J]. Chinese Journal of Underground Space and Engineering, 2009,5 (5):941- 945.

[13] 范刚，张建经，付晓,等. 含泥化夹层顺层岩质边坡动力响应大型振动台试验研究[J]. 岩石力学与工程学报, 2015, 34(9): 1750-1757. FAN Gang，ZHANG Jianjing，FU Xiao, et al. Large-scale shaking table test on dynamic response of bedding rock slopes with silt intercalation [J].Chinese Journal of Rock Mechanics and Engineering.2015,34(9):1750-1757.

[14] 侯伟龙.陡倾层状岩质边坡的大型振动台物理试验研究[D].成都：成都理工大学, 2011. HOU Weilong.Research on large-scale shaking table physical simulation experiment of steep-dipping stratified rock slope[D]. Chengdu: Chengdu University of Technology, 2011.

[15] 刘汉香.基于振动台试验的岩质斜坡地震动力响应规律研究[D].成都：成都理工大学, 2014. LIU Hanxiang. Seismic responses of rock slopes in a shaking table test[D]. Chengdu: Chengdu University of Technology, 2014.

Shaking table test for high slope destruction under earthquake action

YAN Kunfa1，LU Jianhua2，LIU Xiaoyan1，ZHOU Zhijun1

(1. Key Lab of Highway Engineering in Special Region of the Ministry of Education,Chang’an University, Xi’an 710064,China;2. Shaanxi Provincial Auditoffice, Xi’an 710002,China)

Based on the shaking table model test, this paper discusses characteristic and failure mechanism of high slope of structures with weak interlayer surface and different slope forms. The influence of geological conditions and seismic loads on the failure deformation of the slop is also investigated. The experimental results show that the location of mud soft interlayer is easy to occur slip failure. The damage of convex slope mainly includes the collapse of slope shoulder and the integral slippage of the block above the variable slope line. Corresponding failure mechanism mainly is the top of the slope shoulder slipping off slope body. While the damage of convex slope mainly includes the collapse along the variable slope line and relative failure mechanism mainly is the variable slope line on tensile fissure driving the interface model of variable line cut-off collapse. The stability of convex slope is better than concave slope. The greater intensity of vibration results in more significant slope failure. The slope failure is more severe when the frequency is more close to that of the slope model. The duration is closely related with total energy of earthquake input.

high slope; slope shape ；shaking table test；dynamic failure；seismic load

2016-03-03

交通部科技资助项目(2008353361420)

周志军(1975-)，男，江苏泰州人，教授，博士，从事杭基础、特殊土路基及地基处理、边坡稳定性评价与防护设计研究；E-mail：zhoujun9586@163.com

TU393.3

A

1672-7029(2016)12-2396-09