基于PFC3D的浅圆仓偏心卸料离散元研究
程奇鹏, 孙巍巍, 卢 赛
(南京理工大学 理学院, 江苏 南京 210094)
基于PFC3D的浅圆仓偏心卸料离散元研究
程奇鹏, 孙巍巍, 卢 赛
(南京理工大学 理学院, 江苏 南京 210094)
在筒仓试验的基础上建立浅圆仓的PFC3D离散元模型,比较了满仓状态下仓壁侧压力的模型计算值、试验值、规范计算值,模型拟合效果良好,证明了PFC3D能较准确的模拟仓壁侧压力,模型参数选择合理。从颗粒速度场、力场两个角度分析了高径比0.75的浅圆仓偏心率为0.3的偏心卸料过程,发现浅圆仓内贮料不同于深仓中的整体流动特征,呈现的是漏斗状的偏心卸料模式。偏心卸料过程中,仓壁会出现超压现象,超压系数最大值达到1.25。仓壁侧压力参数分析结果表明,仓壁同一位置超压系数随着卸料速度的增大而增大,随着偏心率的增大而增大。在小偏心和低卸料速度的前提下,浅圆仓仓壁设计可不考虑超压现象。结论可供工程设计和以后的研究参考。
浅圆仓; PFC3D; 离散元; 偏心卸料; 侧压力; 参数分析
偏心卸料很早就存在于筒仓的设计、建造和使用中,近年来其重要性和对结构的危害逐渐被人们所认识,也得到各国规范不同程度的重视[1~3]。随着计算机技术的不断发展,研究者们更青睐于采用数值模拟分析方法,目前的数值模拟方法主要有有限单元法[4,5]和离散单元法两种。由于筒仓贮料为散体,其物理性质介于固体和液体之间,用ANSYS等有限元软件很难分析散体的具体颗粒问题,而采用三维颗粒流程序PFC3D能更好的分析颗粒流态、力场、速度场以及偏心卸料超压等问题[6]。
本文以高径比为0.75试验筒仓模型为原型,采用PFC3D中的线性接触刚度模型[7,8]对筒仓的偏心卸料过程进行模拟,大致分为两步:首先对所建立的PFC3D模型进行校核,比较满仓状态下仓壁侧压力模型计算值、试验值和规范值,基本吻合后进行后续动态卸料模拟,监测卸料过程中颗粒的运动、仓壁的受力状态,并进行相关参数分析。
1 模型的建立
在建模之前,先进行了筒仓缩尺试验,筒仓仓壁选用有机玻璃,贮料采用了石英砂,筒仓及贮料相关参数如表1、2所示,试验模型如图1所示。试验通过在筒仓内壁上布置传感器(每列7个)来测取侧压力。本文参照筒仓缩尺试验,利用PFC3D建立了对应的离散元模型。

表1 筒仓模型几何参数

表2 贮料材料特性

图1 试验模型
为了提取不同位置的模拟结果,本文在仓壁环向方向建立20面监测墙,竖向方向建立10面监测墙,共计200个监测点,筒仓模型如图2。

图2 筒仓墙体模型
在PFC3D建模中,遇到的最主要问题是筒仓仓壁和颗粒刚度的取值以及颗粒粒径和级配的选择。本文做法是先根据计算机运行能力和计算精度要求,选择合适的仓壁和颗粒刚度,再对颗粒粒径和数量进行探索,实践过程中发现,刚度的数量级基本要保持在104~105之间。文献[9,10]表明:颗粒的法向刚度大于切向刚度,且处于同一数量级上,一般情况下,颗粒的法向和切向刚度之比在2~6之间,本文将此比值定为2,墙体刚度与颗粒刚度之比一般在1~5左右。不断的计算调试后,确定颗粒和仓壁刚度如表3所示。由于颗粒尺寸大小及颗粒级配决定了侧压力模拟的精度,颗粒直径越小,模拟得到的仓壁侧压力就越精确,但是会极大地增加计算时间;颗粒直径越大,则仓壁侧压力值离散性较大。如果按照试验得到的石英砂粒径,计算达到收敛的时间可能达到数百小时甚至更长时间。经过反复尝试,贮料颗粒半径大小为10~12 mm,颗粒的空隙率设为0.3,将计算时间控制在可接受范围之内。

表3 仓壁、颗粒刚度 N/m
2 满仓静态数值模拟分析
模型生成颗粒之后,对颗粒系统赋予重力加速度,再给定足够多的循环步数,让颗粒系统完全达到稳定状态。在对整个装料模拟过程中,通过观察颗粒系统不平衡力以及仓壁监测墙侧压力变化曲线来判断系统是否达到平衡状态。
图3展示的是满仓状态下离散元模型模拟的筒仓仓壁侧压力值与试验值以及规范[1]计算值的对比图,可以看出,离散元模拟的仓壁侧压力在筒仓底部与试验数据更加接近,在筒仓上部和中部,模拟值与试验数据有点偏差。总的来说,模型拟合效果还是不错的,这表明PFC3D能较好的模拟仓壁侧压力,模型选取的参数是合理的。

图3 满仓下筒仓仓壁侧压力对比
3 偏心卸料数值模拟分析
3.1 贮料流态
筒仓贮料流态一直是大家关心的问题,筒仓卸料的流动形态一般是以下四种中的一种或几种:整体流动、漏斗型流动、管状流动、扩散流动[11]。利用PFC3D进行筒仓卸料的数值模拟,可以很直观、清楚地观测到仓内贮料的流动状态和卸料完成后仓内贮料的堆积状态。
图4展示的是筒仓偏心卸料过程中贮料速度矢量图,卸料初期,颗粒的速度场区域只局限于卸料口附近范围内,随着卸料的不断进行,颗粒速度场通道是顺着卸料口方向向上延伸至贮料顶部,流动通道由管状形态转变为漏斗状形态,颗粒流动速率逐渐变小,颗粒沿着卸料孔上方的这个管状通道向下快速流动,部分存在于筒仓底部区域的颗粒很难流出仓内,该部分颗粒俗称死料。比较图4a~j中不同颜色颗粒消失顺序,可以将浅圆仓偏心卸料模式概括为:卸料口处颗粒最先卸出,贮料上表面下降,仓顶颗粒最先流入卸料通道并流出卸料口外。
图5展示的是卸料过程中离散元模拟的贮料形态与试验观察形态对比图。模拟结果与试验结果吻合较好。卸料过程中,仓顶颗粒不断地向卸料口流动,呈现漏斗状的偏心卸料模式,仓底部分贮料是基本不动的,这与深仓卸料过程中贮料的整体流动特征是不同的。

图4 偏心卸料过程中贮料速度矢量

图5 颗粒流态的数值模拟与试验观测结果对比
3.2 颗粒力场
图6展示的是浅圆仓在偏心卸料过程中颗粒之间接触力场变化示意图,打开卸料口时,位于卸料口上方的颗粒之间接触力明显减小,随着卸料的进行,靠近卸料口的仓壁右侧接触力场减小比较明显。对比图4和图6可以看出,流速大的区域(卸料通道区域)对应的接触力线稀疏,流速小的区域对应的接触力线密集。浅圆仓内颗粒接触力场不同于深仓,在卸料口上方不存在压力拱,更没有压力拱被破坏。
3.3 仓壁侧压力
为了研究方便,下文从各列监测墙中选取6个监测点数据进行后续的数据处理。
图7展示的是A列(靠近卸料口)不同高度监测墙动态侧压力曲线,刚开始有一段比较平稳的直线,表明筒仓内颗粒系统此时已经达到满载平衡状态。卸料初期,筒仓中下部测点侧压力迅速下降,随后监测墙的侧压力上下波动明显,筒仓上部测点侧压力在卸料口打开瞬间出现短暂的超压现象,随后迅速下降,超压原因可能是:离散元模型选取的颗粒直径比试验贮料直径大,卸料口打开瞬间仓内颗粒流向卸料口时,颗粒对上部近侧仓壁的挤压以及冲击比较明显。图8展示的是B列(与A列呈30°夹角)不同高度监测墙动态侧压力曲线,卸料口打开瞬间,仓壁侧压力迅速降低,但很快呈现出仓壁侧压力慢慢增大现象,随着卸料的进行,仓顶贮料面不断降低,仓壁侧压力缓慢减小,侧压力波动不明显,各位置侧压力峰值出现的时间是不同的。超压系数最大值为1.25,超压测点位于仓壁中上部。

图7 A列不同高度监测墙动态侧压力曲线

图8 B列不同高度监测墙动态侧压力曲线
将A、B两列监测墙在卸料过程中的侧压力超压系数绘成图9。B列监测墙超压区域多于A列,超压位置均位于筒仓中上段,越往上超压越明显。

图9 不同高度监测墙超压系数
3.4 仓壁侧压力参数分析
为了研究卸料速度对筒仓仓壁侧压力超压系数的影响,保持偏心率0.3不变,通过改变卸料口大小来调整卸料速度,使卸料口半径r分别达到0.05,0.10,0.15,0.20 m。图10展示的是不同卸料口大小对应的A列和B列各位置的侧压力超压系数。当卸料口较小时,超压不明显,随着卸料口半径的增大,即贮料卸料速度的增大,各监测墙位置超压系数都在增大,仓壁中下部基本不产生超压现象。对比两图发现,B列监测墙比A列监测墙超压区域更大,最大超压系数达到1.31,A列监测墙超压系数波动比较明显,可能是因为A列距卸料口更近,贮料颗粒冲击效果更明显。

图10 不同卸料口大小对应的A、B两列监测墙侧压力超压系数
为了研究偏心率e/d对筒仓仓壁侧压力超压系数的影响,卸料口大小保持不变,模拟了六种不同偏心率的卸料过程。图11展示的是不同偏心率卸料过程中A、B两列监测墙侧压力超压系数。偏心率较小时,基本不会出现超压现象,随着偏心率的增大,超压系数都是增大的,B列监测墙比A列更容易产生超压现象,超压位置基本都在仓壁中上部。图11a中,当偏心率达到0.25时筒仓开始出现超压现象,最大超压位置位于筒仓上部,超压系数为1.04。图11b中,当偏心率达到0.20时开始出现超压现象,最大超压位置也是在筒仓上部,超压系数为1.07。
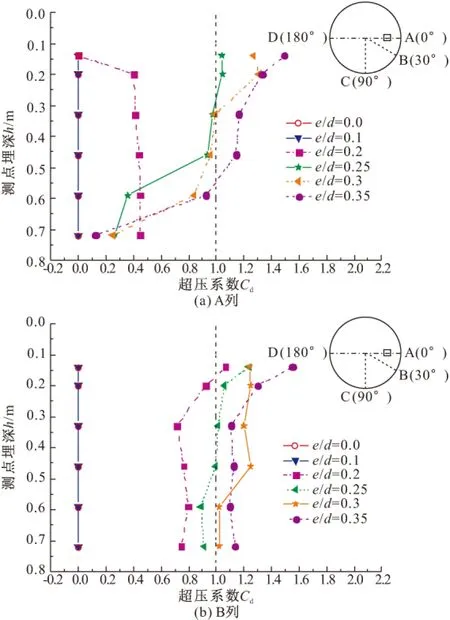
图11 不同偏心率对应的A、B两列监测墙侧压力超压系数
4 结论
(1)满仓状态下,浅圆仓侧压力离散元模拟值与试验值以及规范值较为吻合,说明PFC3D模型所选取的参数是合适的。从颗粒速度场、力场两个角度对浅圆仓偏心卸料过程的分析表明,浅圆仓贮料呈现漏斗状的偏心卸料模式,区别于深仓贮料整体流动特征。
(2)偏心卸料下,动态侧压力峰值出现在卸料初始阶段,超压位置基本只在筒仓中上部,最大
超压系数达到1.25,靠近卸料口的A列侧压力的大幅度波动可能是大颗粒贮料对仓壁的撞击造成的。
(3)参数分析表明,偏心卸料下,随着卸料口半径的减小,即贮料卸料速度的降低,同一监测点侧压力超压系数在减小;随着偏心率的增大,同一监测点超压系数也在增大。而实际工程中,浅圆仓卸料速度很低,小偏心卸料浅圆仓仓壁设计时可以不考虑超压现象。
[1] GB 50077-2003, 钢筋混凝土筒仓设计规范[S].
[2] DIN EN 1991-4(2006-12), Eurocode 1: Actions on Structures-Part 4: Silos and Tanks[S].
[3] AS 3774-1996, Loads on Bulk Solids Containers[S].
[4] 林 红, 魏文晖, 胡智斌, 等. 钢筋混凝土筒仓库侧卸料静动态压力分布研究[J]. 土木工程与管理学报, 2014, 31(2): 29-33.
[5] Ding S, Li H, Ooi J Y, et al. Prediction of flow patterns during silo discharges using a finite element approach and its preliminary experimental verification[J]. Particuology, 2015, 18(1): 42-49.
[6] Djordjevic N, Shi F N, Morrison R. Determination of lifter design, speed and filling effects in AG mills by 3D DEM[J]. Minerals Engineering, 2004, 17(11): 1135-1142.
[7] 王婷婷. 离心模型筒仓内散体物料压力的数值模拟研究[D]. 郑州: 河南工业大学, 2005.
[8] 焦红光, 李靖如, 赵继芬, 等. 关于离散元法计算参数的探讨[J]. 河南理工大学学报(自然科学版), 2007, 26(1): 88-93.
[9] 邢纪波, 俞良群, 张瑞丰, 等. 离散单元法的计算参数和求解方法选择[J]. 计算力学学报, 1999, 16(1): 47-51.
[10]吴爱祥, 孙业志, 刘湘平. 散体动力学理论及其应用[M]. 北京: 冶金工业出版社, 2002.
[11]丁盛威. 基于PFC3D的筒仓贮料侧压力离散元分析[D]. 武汉: 武汉理工大学, 2014.
Discrete Element Analysis of Squat Silo Under Eccentric Discharge by PFC3D
CHENGQi-peng,SUNWei-wei,LUSai
(School of Science, Nanjing University of Science and Technology, Nanjing 210094, China)
Based on silo experiment, a discrete element model of squat silo was made by PFC3D. The comparison about lateral pressure among model, experiment and standard in full load condition shows a good simulated effect in the model, which proves that lateral pressure can be simulated by PFC3D accurately and parameter choose of the model is reasonable. From the analysis about squat silo with 0.75 height-to-diameter ratio and 0.3 eccentricity under eccentric discharge on velocity field and stress field, eccentric discharge model of funnel shape about stored material is found in squat silo, which is different from bulk flow characteristic in deep silo. Over-pressure phenomenon is found on the silo wall during the process of eccentric discharge and the maximum of over-pressure coefficient is 1.25. The results of parameter analysis about the lateral pressure show that the over-pressure coefficient will increase with the increase of the eccentric discharge speed and the eccentricity. In premises of small eccentricity and low discharge speed, over-pressure phenomenon can be ignored about the design of squat silo wall.The conclusion can be reference for the engineering design and the future research.
squat silo; PFC3D; discrete element; eccentric discharge; lateral pressure; parameter analysis
2016-03-27
2016-05-31
程奇鹏(1992-),男,安徽安庆人,硕士研究生,研究方向为筒仓结构工程(Email:2715480212@qq.com)
孙巍巍(1979-),男,江苏淮安人,副教授,博士,研究方向为结构工程(Email:sww717@163.com)
国家自然科学基金(51308297);江苏省普通高校学术学位研究生创新计划项目(KYLX15_0408)
TU359
A
2095-0985(2016)06-0043-05

