转子偏心下环模制粒机的振动分析与结构优化

沈江飞， 武 凯， 崔先岸， 孙 宇

(南京理工大学 机械工程学院，南京 210094)

转子偏心下环模制粒机的振动分析与结构优化

沈江飞， 武 凯， 崔先岸， 孙 宇

(南京理工大学 机械工程学院，南京 210094)

环模制粒机因其高效率、低能耗等优点广泛应用于饲料、生物质能源等领域，而目前的环模制粒机振动剧烈，尤其是有转子偏心时环模会受到强烈的振动冲击，严重减小环模的使用寿命。因此对转子偏心下环模制粒机的振动特性进行了分析并对其主要结构进行优化。基于粉体挤压成型规律以及环模与压辊挤压成型规律，建立了考虑压辊表面正向静摩擦力作用下的环模与压辊之间准确的相互作用力模型，并对压辊与环模有相对位移时其相互作用力的变化规律进行建模和分析。基于多体动力学软件建立了转子偏心下环模制粒机的动力学仿真模型，分析转轴、主轴以及挤压力的振动特性，并对主轴、支撑架以及转轴轴承的结构或位置参数进行分析和优化。研究结果表明：压辊与环模之间相互作用力与相对位移之间近似成线性关系；主轴上转轴支撑段直径应大于直径；主轴直径增大有利于转轴振动幅值减小但是会增大挤压力幅值，将压辊底座通过柔性杆与主轴连接可在减小转轴振动的同时大幅减小挤压力的振动；支撑架的径向刚度应大于1×107N/m,弯矩刚度应大于1×105N·m/deg；转轴轴承间距存在与轴承刚度相关的最优值，且最优轴承间距会随着轴承刚度增大而减小。

环模制粒机；转子偏心；动力学仿真；粉体挤压；振动

环模制粒机是一种高效的粉体挤压制粒成型装备，具有制粒过程稳定，生产效率高、能耗低等优点。在饲料加工领域，环模制粒机是饲料机械的四大主机之一，具有成型率高、提高动物生长性能等一系列优点[1]。目前环模制粒机的设计大部分还是依靠经验数据，而国外制粒机发展历史久，设计经验丰富，因而国内制粒机的设计一直处于劣势。随着目前国内制粒机向着大功率、精细化的方向发展，对其动态特性的要求也越来越高。环模制粒机由于其独特的悬臂支撑的结构特点，支撑刚度低，定、转子之间定位精度差，因而当转子偏心时制粒机会发生剧烈振动。环模制粒机使用过程中转子组件中的环模因其易损性需经常更换，而其安装精度很难保证，因而建立准确的环模制粒机负载力学模型以及其系统动力学模型，对其结构参数进行优化，减小因转子偏心造成的振动危害是环模制粒机在设计时急需解决的问题。

目前国内外对环模制粒机研究主要集中于其静力学特性的研究[2-7]，颗粒质量[8-9]，加工工艺参数[10-11]以及核心部件磨损[12-13]的研究；对其动态特性的研究较少，其中彭建云[14]对环模制粒机转轴零件的瞬态响应过程进行了分析，武凯等[15]对环模制粒机在空载情况下的环模制粒机振动进行了实验分析。在粉体旋转挤压力学模型方面，武凯等[2]对环模的扭矩进行了理论和实验分析，建立了变形压紧区和挤出区的挤压力模型；HOLM等[7]研究了环模挤压木屑过程的挤压力和扭矩模型；但上述分析都未考虑压辊表面的正向摩擦力作用以及粉体挤压力与相对密度之间关系规律曲线。在粉体压缩力学模型方面，BINDHUMADHAVAN等[16]对双滚轮挤压粉体成型进行了实验分析，得到滚轮表面压力的对数值与粉末的相对密度的对数值成线性关系;STEFANIE等[17]在分析药物助型剂挤压成型时用指数模型拟合挤压力与密度的关系；吴劲峰等[18]对苜蓿草粉制粒密度与挤出力的关系进行了仿真实验得到挤压力与密度近似为指数关系。以上研究对于探究环模制粒机的振动特征具有重要意义，但目前国内外还未见关于环模制粒机转子偏心下振动的研究。

本文以双压辊带式环模制粒机为对象，对其在转子偏心下的振动情况进行研究，分析环模制粒机重要结构参数对振动的影响规律。

1 环模与压辊之间相互作用力模型

挤压力波动是转子偏心下环模制粒机振动的主要原因，因此建立准确的环模与压辊挤压区的相互作用力模型是分析其振动特性的关键。如图1所示，环模制粒机是靠环模与压辊之间啮合转动，将环模的转动扭矩转变为挤压力将物料挤压成型。环模与压辊之间的挤压区可分为攫取区、压实区和挤出区，物料在攫取区被攫入模辊间隙，经过压紧区压实至挤出密度，物料在挤出区被挤入环模模孔中成型后挤出，经割刀割断后成柱状颗粒。

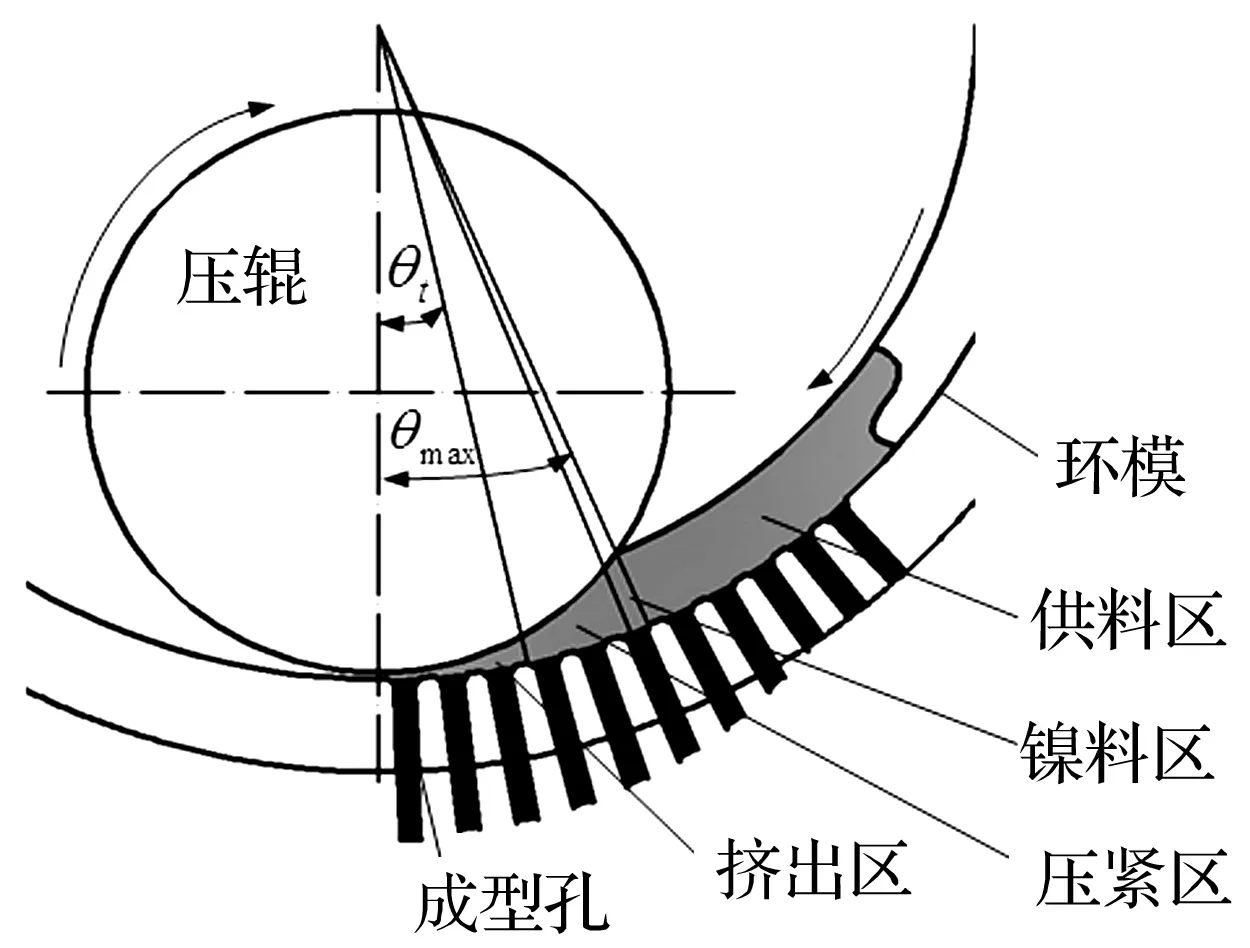
注：θt为挤出区角度，θmax为整个挤压区角度图1 环模制粒机成型过程示意图Fig.1 Molding process sketch map of ring die pellet mill

挤压力波动是转子偏心下环模制粒机振动的主要原因，因此建立准确的环模与压辊挤压区的相互作用力模型是分析其振动特性的关键。环模制粒机是靠环模与压辊之间相向转动，将环模内表面的物料挤进模孔后经短暂保压后挤出成为柱状长条，然后经割刀割断形成柱状短颗粒。环模与压辊之间的挤压区可分为攫取区、压实区和挤出区，物料在攫取区被攫入模辊间隙，经过压紧区压实至挤出密度，物料在挤出区被挤入环模模孔中成型后挤出。在压紧区环模内表面所受物料压紧力随着物料密度增大而不断增加，在达到挤出压力Pt后进入挤出区，此时物料密度和压紧力都不再继续上升。

挤压制粒过程中，物料在压辊的攫取作用下进入挤压区，因而压辊表面会受到物料的负摩擦力作用；但是由于压辊的转动并没有主动驱动装置，压辊实际是在挤压区物料和环模的正向摩擦力作用下发生转动，因而压辊表面同时作用有两个方向的摩擦力。而目前学者分析研究挤压区受力模型时都未考虑压辊表面的正向摩擦力作用。

环模与压辊挤压区中最小间隙处粉料密度最大，此处环模与压辊之间接触刚度大，正常工作时环模与压辊之间静摩擦力很大，足以阻止压辊与环模之间的相对滑动趋势，因而压辊转动线速度与环模转动线速度大小相同。环模内部挤压区物料沿压辊切线方向速度则小于压辊转速，因此物料有相对于压辊向后运动趋势，因此可知压辊表面受到物料的摩擦力方向与转动方向相反，为负摩擦力。而压辊与环模最小间隙处的摩擦力驱动压辊发生转动，摩擦力方向与压辊转动方向一致，为正向摩擦力。若不计物料惯性力，假设环模与压辊近似为刚性体，可将环模的受力移至环模中心得到受力分析图见图2。其中，Fcy为环模表面所受物料压力y向分量，Fcz为环模表面所受物料压力z向分量,fy为环模表面所受物料摩擦力y向分量，fz为环模表面所受物料摩擦力z向分量,Mf为物料对环模的摩擦力扭矩，Ff为压辊驱动力的反作用力，e为压辊与环模中心距离，rh为环模内径，rr为压辊外径，d为缓冲层物料厚度，h为供料区物料厚度。

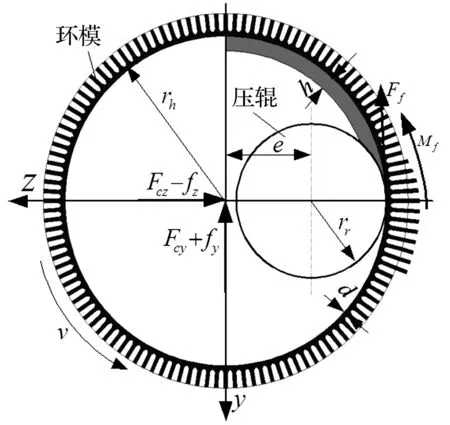
图2 环模受力分析图Fig.2 Analytical graph of the interaction force of ring die

压辊受力应与环模上作用力大小相同，方向相反，且稳定运行时压辊转速稳定，因而压辊所受扭矩总和应为零，即有：

(1)

式中环模所受物料的摩擦力矩Mf的计算方法目前主要是有限元法[20-22]、片体分析法[23-24]和离散单元法(DEM)[25-26]，这三种方法分析过程复杂，计算困难，也有使用摩擦因数法的摩擦力矩计算[2-7,14-15]，但摩擦阻力实际为静摩擦力，其摩擦因数的确定困难。实际运行时的挤压区很小，因而挤压区摩擦力的z向分力fz相比y向分力fy以及压力Fcz可忽略不计，环模所受非最小间隙处粉料的摩擦扭矩可近似表示为Mf≈fy·rh。则压辊与环模之间总的相互作用力可表示为作用于压辊中心的两个正交分量Fy和Fz：

Fy=Fcy+fy+Ff=Fcy+

Fz=Fcz

(2)

粉体物料在受滚轮挤压时，压紧区物料主要发生体积塑性应变[20-24]，因而压紧区各位置处物料密度与压辊和环模之间的间隙沿环模内表面法向的高度值成反比。为减小压辊以及环模的磨损与冲击，压辊安装时会在压辊与环模之间留有间隙，因此环模与压辊挤压物料时，一部分物料会滞留在环模内表面而形成保护环模免受冲击磨损的缓冲层。缓冲层的物料密度为挤出密度，挤压时其密度不再增加，因而物料的压缩仅限于发生在缓冲层之上。则根据图2可计算的压紧区中缓冲层之上的物料密度与初始密度的比值γ(θ)与环模圆心角θ的关系如式(3)所示。

(3)

众多压缩实验[17-26]表明粉体物料在挤压成型时其挤压力与物料密度有着稳定的函数关系，因此可以利用粉体物料这种独特的性质，根据压辊表面物料的相对密度来估计相应位置处的挤压力大小，从而简单有效的计算出环模和压辊的受力状态。挤压力与物料密度的关系函数此处采用应用范围广泛的指数模型，即有：

P(γ)=λek(γ-1)

(4)

式中，λ和k为常数。

因此可根据式(3)、式(4)得到缓冲层内表面压紧区压应力与环模圆心角的函数关系为：

P(θ)=λek[γ(θ)-1]

(5)

考虑到缓冲层内外表面大小不同，因此若需环模内表面压力到达挤出力Pt，缓冲层内表面挤出区的法向压力值需达到的压力值应大于挤出力，其值需按式(6)计算。

(6)

攫取区中压辊主要受物料惯性力作用，其作用力很小，分析时忽略其影响。则式(2)中环模与压辊的相互作用力分量Fcy和Fcz可通过对环模内表面缓冲层上压紧区和挤出区的压力在y轴和z轴向的分量进行积分得到，其积分表达式如式7所示。

(7)

根据图2可得式(7)中挤压区最大圆心角θmax的计算公式为：

(8)

同理可得挤出区圆心角θt的计算公式为：

(9)

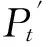
(10)

上述方法虽然使得压辊与环模的相互作用力大小能够通过较为简单的理论计算得到，但是若需要进行动力学分析，其计算量依然十分巨大，无法直接使用进行动力学分析。环模制粒机使用前需对压辊进行调心，将压辊与环模之间的间隙调整至合适值，因此当转子偏心转动时，压辊组件中心与转子转动中心不重合，压辊与环模之间会发生相对位移。当压辊与环模有相对运动位移dy和dz时，压辊与环模之间的动态偏心距值可表示为：

(11)

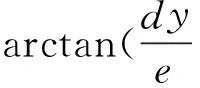
图3 不同dy下的Fy与Fz及拟合函数Fig.3 Value of Fy and Fz under different dy, and the force-displacement fitting functions

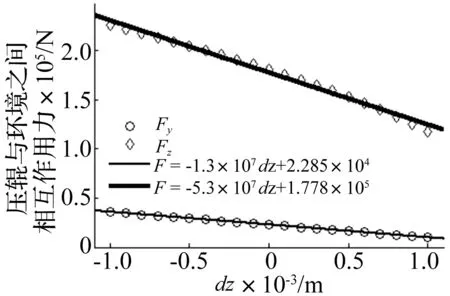
图4 不同dz下的Fy与Fz及拟合函数Fig.4 Value of Fy and Fz under different dz, and the force-displacement fitting functions

由图3和图4可见当压辊与环模有y和z轴向相对位移且位移较小时，压辊与环模之间的相互作用力与y和z轴向的相对位移之间近似为线性关系。而当压辊与环模之间有x向相对小位移时，由于环模宽度大于压辊，因此挤压力不受影响，且当压辊倾斜时产生的x轴分力也会被压辊与环模之间轴向摩擦力平衡。因而根据上述分析在相对位移较小时可将压辊与环模之间相互作用力与相对位移的关系等效为如式(12)所示的等效线性化关系模型。

(12)

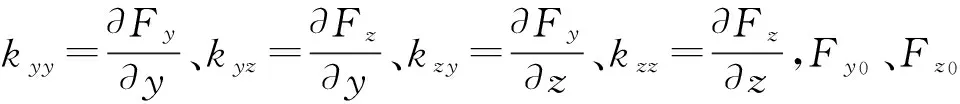
2 环模制粒机动力学仿真模型

图5为带式环模制粒机结构示意图，环模制粒机主要包括转子组件、定子组件、支撑组件以及动力系统[27]；转子组件主要包含转轴、带轮、环模、落料环等，定子组件主要包括主轴、压辊组件等，支撑组件包括支撑架，动力组件包括电机和传动系统。

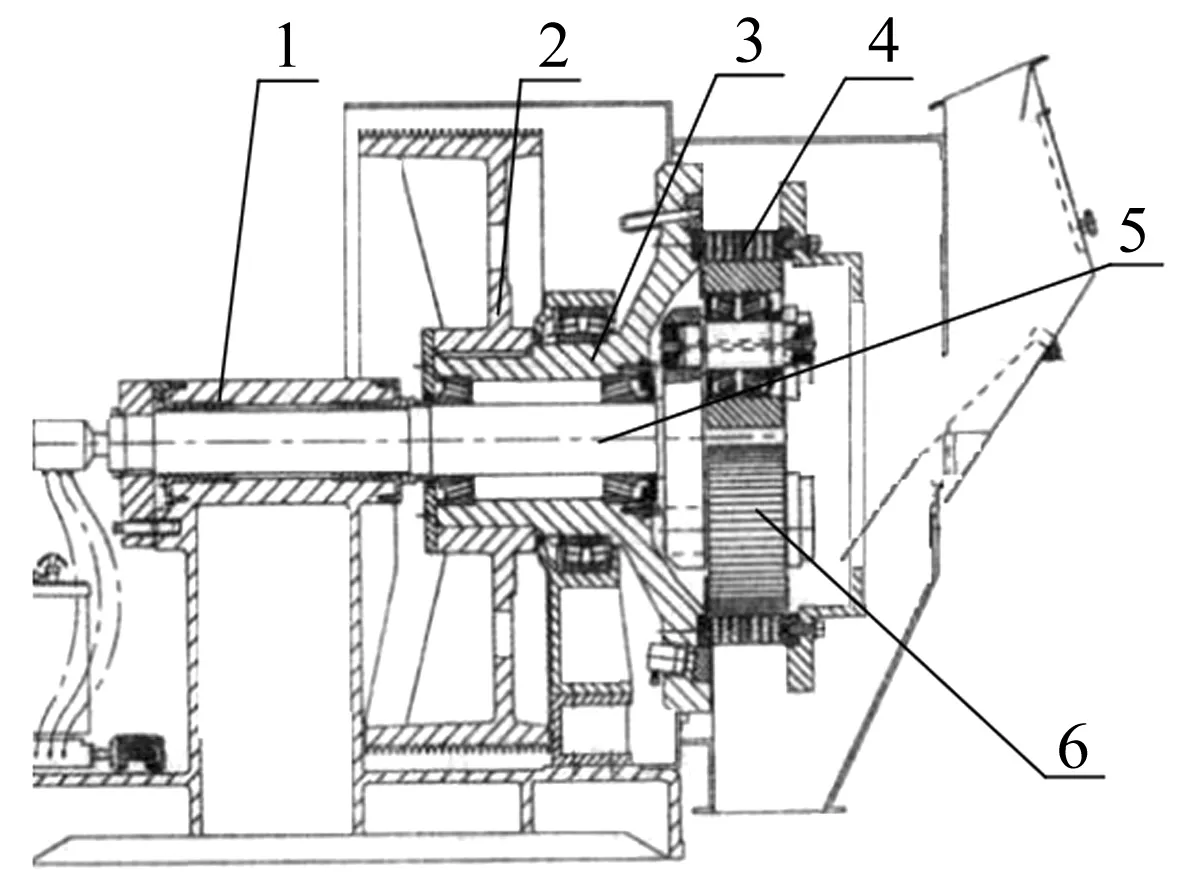
1.支撑架2. 带轮 3. 转轴 4. 环模 5.主轴6. 压辊 图5 带式环模制粒机结构示意图Fig.5 Schematic diagram of draper-type ring die pellet mill

环模制粒机的主轴为悬臂支撑轴，振动时会产生较大弹性变形，而目前针对弹性悬臂梁支撑的定转子相互作用下的动力学理论分析模型[28]计算复杂，且需对实际结构做大幅理想化处理。环模制粒机的转轴支撑轴承跨距大，主轴弹性变形大，部件众多且部件之间接触关系复杂，手工推导动力学模型需要大量复杂的代数计算和微分运算，因此采用多体系统动力学方法解决复杂系统的动力学问题成为一种必然的选择[29]。

为得到与实际情况相匹配的结论，根据图5中环模制粒机的结构特点，运用多体动力学软件adams建立更为准确实用的环模制粒机动力学仿真模型。目前带式环模制粒机的支撑架种类多样，有焊接钢架、铸件、黏土类支架等，为研究各个部件特性对系统振动的影响规律，模型中用轴套力代表支撑架的支撑作用；主轴的弹性变形环模制粒机振动的主要形式，为便于模型的参数化以及分析方便，用等效的多段梁表示主轴的弹性支撑作用[30]；其他部件因变形微小，视为刚性体；为减小计算量，将众多微小零件视为主体部件的几何特征；主要零件的连接根据实际情况使用相应柔性约束，轴承使用柔性轴承，带为刚性带，材料，接触，阻尼以及其他刚性约束等参数根据环模制粒机实际结构确定；环模与压辊之间的相互作用力负载通过两个一般力矢量表达，力矢量的受力物体设为环模，则环模上的受力位置为浮动点，这与实际挤压情况相符，各分力的表达式如式(12)。

转轴组件中的转轴、带轮等组件在环模制粒机的使用中无需调整，因而其偏心可以通过提高制造和安装精度减小到合理范围，但环模的安装偏心则难以控制，因而环模制粒机的转子偏心主要表现为环模的安装偏心。短锥面接触安装因其安装可靠、经济性好等原因，是目前环模安装固定的主流方式，但其安装过程要求严格，若环模安装过程中上下螺栓拧紧方式不正确，极易产生环模安装位置偏心和倾斜。在adams仿真模型中可通过修改模型中环模与压辊上作用力标记点以及环模质心标记点的坐标以表示安装偏心时其对系统振动的影响。

3 动力学仿真分析

取环模安装误差为c=0.001 m，α=10；积分求解器为HHT积分器，积分误差设为1.00×10-6，转轴转动频率为8 Hz，运行时间5 s，在后处理模块观察制粒机模型各零件的振动情况。

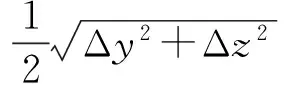
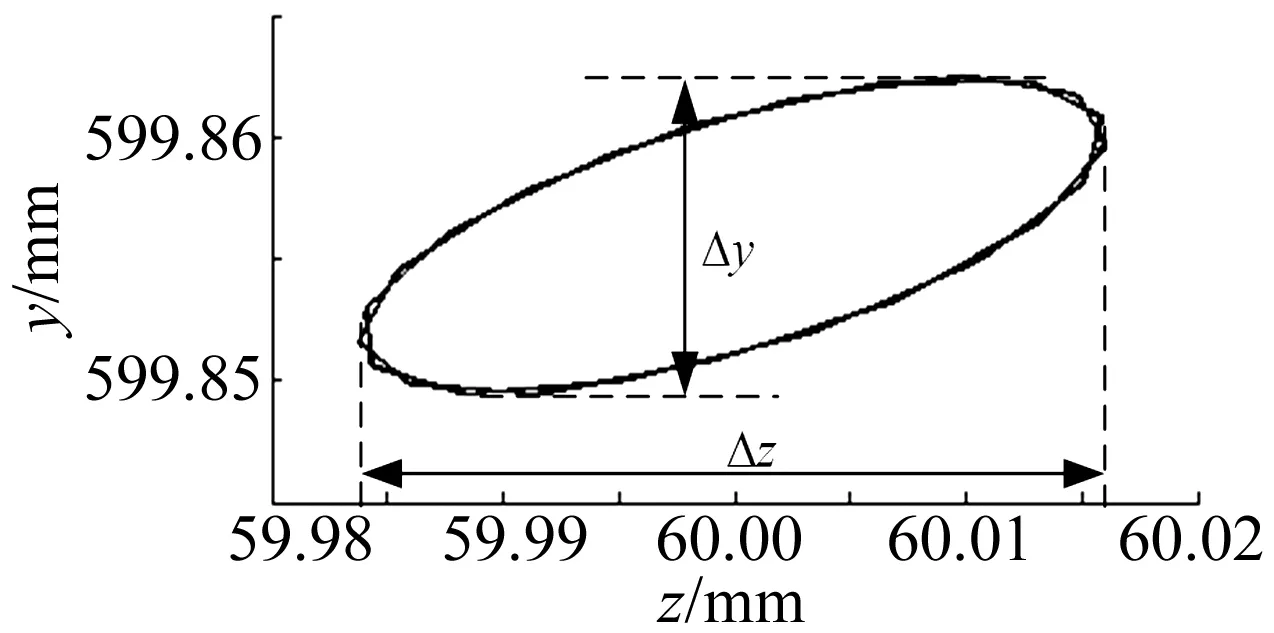
图6 转轴右侧面中心振动轨迹Fig.6 Vibration track of the right side center point of revolving shaft

图7 挤压力振动曲线Fig.7 Vibration curve of compaction forces

图8为主轴从支撑端至压辊安装位置，梁1～7的弯矩振动情况；如图所示，从No.3到No.7，梁的振动幅值快速增大。因而可知主轴支撑端弯矩幅值较小，而从转轴支撑位置开始弯矩迅速增大；这也解释了目前国外机型设计中主轴的末端直径大而支撑端直径较小的原因。

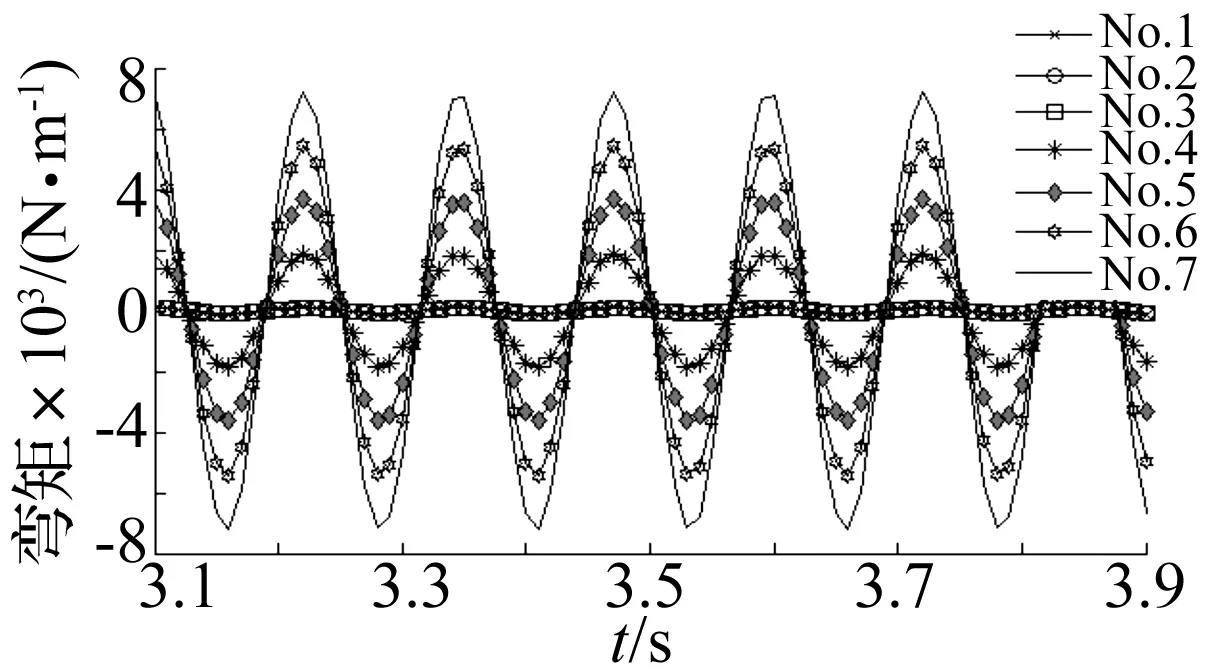
图8 主轴各段梁弯矩Fig.8 Bending moments of each beam in dead axle

3.1 结构参数对振动的影响规律及结构优化

环模是制粒机上最重要的易损件，而转轴以及挤压力的振动会直接加速环模的疲劳磨损和冲击破坏，因而环模制粒机在动态设计时须针对转轴以及挤压力的振动幅值进行结构参数优化。

图9为主轴直径变化时挤压力以及转轴振动幅值的变化情况，由图可见随着主轴直径的增大，虽然转轴振动幅值迅速减小，但是挤压力的振动幅值也会剧烈增加。

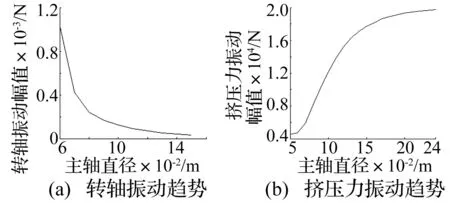
图9 主轴直径对环模制粒机振动影响Fig.9 Effect of dead axle diameter on the vibration of ring die pellet mill

为解决主轴直径增大时转轴振动幅值与挤压力振动幅值呈相反趋势的矛盾，如图10将主轴主体右端缩短至转轴的右支撑位置，将压辊底座通过一个较细的柔性杆固定在主轴右端。

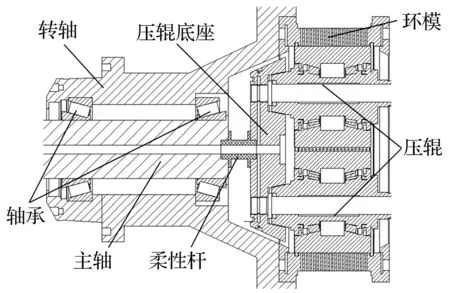
图10 压辊底座支撑结构优化Fig.10 Optimization of the support structure of roller base

图11为优化后转轴的振动以及挤压力振动与优化前的对比，由图可见优化后挤压力振动幅值明显减小，转轴振动也得到一定程度改善。通过对图中轨迹进行测量可发现优化后的转轴振动椭圆轨迹的长轴长度减小了约30%，而挤压力振动幅值则从约40 kN左右降至10 kN左右，减小到优化前的1/4。

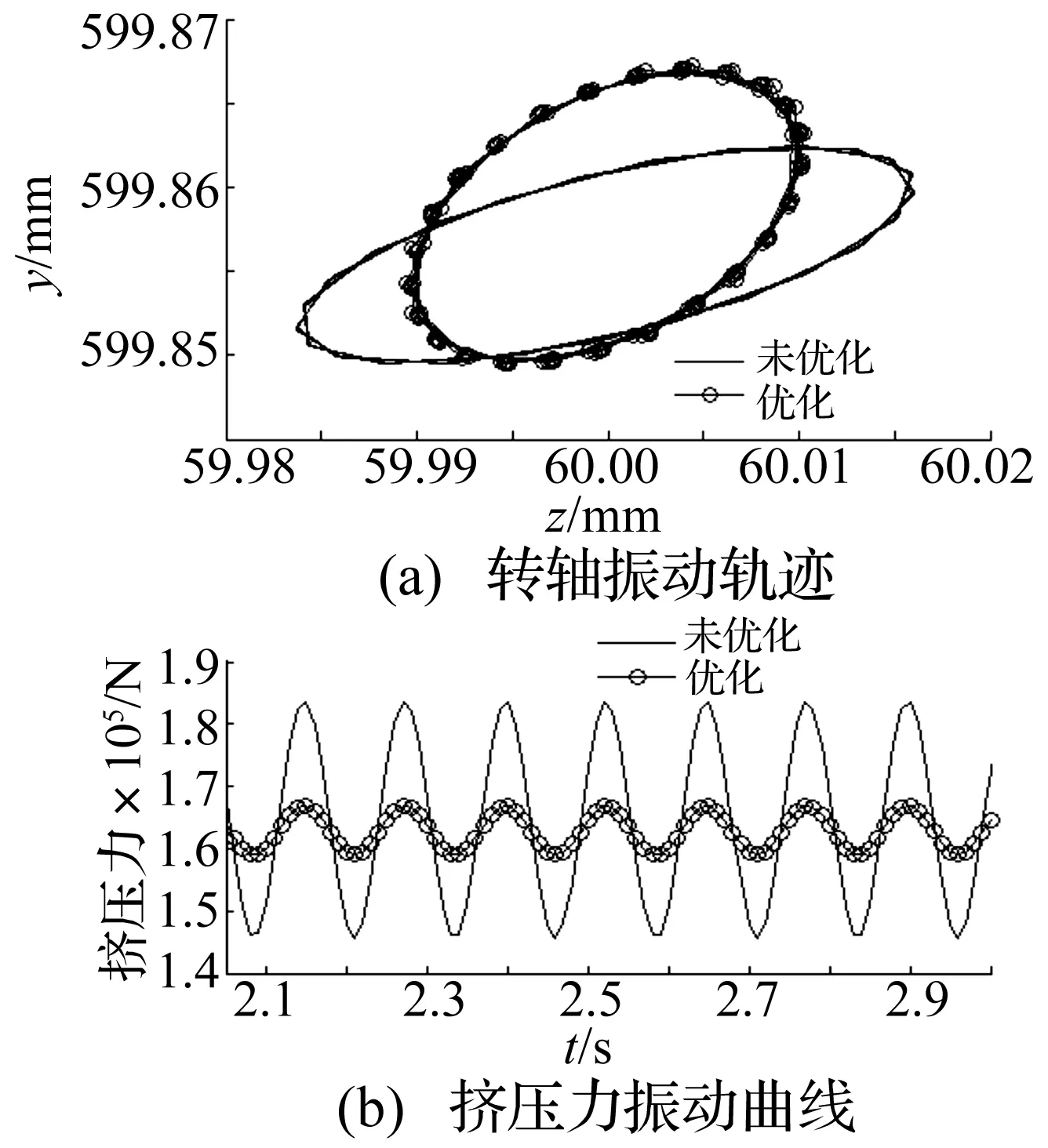
注： 主轴外径0.18 m，柔性杆外径0.04 m图11 优化前后振动对比Fig.11 comparison of vibrations before and after optimization

根据图5的环模制粒机结构简图，由于环模与压辊之间通过主轴相互固定，而支撑架支撑主轴，因而支撑架刚度的变化对环模与压辊之间作用力几乎没有影响，主要影响转轴的振动幅值。图12为支撑架刚度变化时的转轴振动幅值的变化情况，可见随着支撑架弯曲刚度和径向刚度的增加，转轴振动幅值先增大后减小。在支撑架弯曲刚度为1×104或者径向刚度为2×106附近时环模制粒机系统第一阶固有频率靠近转子转动频率，因而转轴振动幅值剧烈增加。根据图12(a)和图12(b)可知为了减小环模制粒机转子偏心时振动危害，支撑架的径向刚度应大于1×107N/m,弯矩刚度应大于1×105N·m/deg。

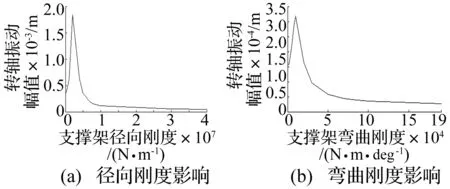
图12 支撑架刚度对转轴振动影响Fig.12 Effect of frame supportting stiffness on the vibration of revolving shaft

转轴的长度是环模制粒机设计时重要的结构参数，其取值主要与转轴支撑轴承的间距有关。图13为不同轴承刚度下转轴轴承间距对转轴振动的影响规律曲线，由图可知在任一轴承刚度下，随着转轴轴承间距的增大，转轴振动幅值都有着先减小后增大的趋势；转轴振动幅值的极小值会随着轴承刚度增大而减小，且转轴振动幅值取极小值时转轴轴承间距的值也随着轴承刚度增大而减小。因而设计时可根据所选用的转轴轴承的刚度，对照图13选择最优的轴承间距，减小转轴的振动幅值。

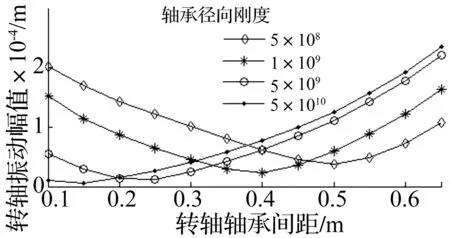
图13 不同轴承刚度下转轴轴承间距对转轴振动影响Fig.13 Effect of bearing spacing on the vibration of revolving shaft in different bearing radial stiffness

4 结 论

为解决转子偏心下环模制粒机的剧烈振动问题，本文建立了环模与压辊之间的相互作用力模型以及动力学模型，并依据模型对环模制粒机的主要结构参数进行了分析，得出以下结论：

(1)环模与压辊之间的相互作用力与相对振动位移之间近似为线性关系。

(2)主轴从转轴左支撑点位置至压辊安装位置弯矩幅值逐渐增大，转轴支撑段弯矩幅值远大于支撑架支撑位置弯矩幅值，主轴上转轴支撑段直径应大于支撑架支撑位置直径。

(3)随着主轴直径增大，转轴振动幅值减小而挤压力幅值增大；将压辊底座的安装方式优化为通过柔性杆与主轴连接可以减小转轴振动幅值的同时大幅减小挤压力的振动幅值。

(4)为减小转轴振动幅值，支撑架径向刚度应大于1×107N/m,弯矩刚度应大于1×105N·m/deg。

(5)随着转轴轴承间距的增大，转轴振动幅值会先减小后增大，转轴振动幅值极小值处的轴承间距为相应轴承刚度下的最优轴承间距；且转轴振动幅值的极小值以及最优轴承间距会随着轴承刚度增大而减小。

[1] BEHNK K C. The art(science) of pelleting[C]// Presented onbehalf of the American Soybean Association. Malaysia & Vietnam, 2005.

[2] 武凯，孙宇，彭斌彬，等. 环模制粒粉体挤压成型扭矩模型构建及实验[J].农业工程学报，2013, 29 (24)：33-38. WU Kai，SUN Yu, PENG Binbin, et al. Modeling and experiment on rotary extrusion torque in ring-die pelleting process[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29 (24): 33-38.

[3] 武凯，施水娟，孙宇，等. 环模制粒挤压过程力学建模及影响因素分析[J].农业工程学报，2010, 26 (12)：142-147. WU Kai，SHI Shuijuan, SUN Yu, et al. Modeling and analysis on extruding force in pelleting process[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(12): 142-147.

[4] 丛宏斌, 赵立欣，孟海波，等. 生物质环模制粒机产能与能耗分析[J].农业机械学报，2013, 44 (11)：144-149. CONG Hongbin, ZHAO Lixin, MENG Haibo, et al. Analysis on capacity and energy consumption of biomass circular mould granulator[J]. Transaction of Chinese Society for Agricultural Machinery, 2013, 44(11): 144-149.

[5] 王春华，宋超，朱天龙，等. 环模秸秆成型机压辊半径的优选与试验[J].农业工程学报，2013, 29 (15)：26-32. WANG Chunhua，SONG Chao, ZHU Tianlong， et al. Optimization and test of roller radius of ring die straw forming machine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(15): 26-32.

[6] 丛宏斌，赵立欣，孟海波，等. 立式环模秸秆压块机成型过程建模与参数优化[J].农业机械学报，2014, 45 (10)：187-192. CONG Hongbin, ZHAO Lixin, MENG Haibo, et al. Process modeling and parameter optimization of straw briquetting machine with vertical circular moul[J]. Transaction of Chinese Society for Agricultural Machinery, 2014, 45(10): 187-192.

[7] HOLM J K, HENRIKSEN U B, WAND K, et al. Experimental verification of novel pellet model using a single pelleter unit[J]. Energy & Fuels, 2007, 21:2446-2449.

[8] ARSHADI M, GREF R, GELADI P, et al. The influence of raw material characteristics on the industrial pelletizing process and pellet quality[J].Fuel Processing Technology,2008, 89(12): 1442-1447.

[9] GARCIA-MARAVER A, POPOV V, ZAMORANO M. A review of European standards for pellet quality[J]. Renewable Energy, 2011, 36(12): 3537-3540.

[10] 陈树人，段建，姚勇，等. 环模式成型机压缩水稻秆成型工艺参数优化[J]. 农业工程学报，2013, 29 (22)：32-41. CHEN Shuren, DUAN Jian, YAO Yong, et al. Optimization of technique parameters of annular mould briquetting machine for straw briquette compressing[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013 29(22): 32-41.

[11] 庞利沙，孟海波，赵立欣，等. 立式环模秸秆压块成型机作业参数优化[J]. 农业工程学报，2013, 29 (23)：166-172. PANG Lisha, MENG Haibo, ZHAO Lixin, et al. Optimization of operating parameters for vertical ring mold straw briquetting machine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29 (23)：166-172.

[12] 夏先飞，孙宇，武凯，等. 秸秆压块机组合环模的磨损机理[J]. 农业工程学报，2014，30(4)：32-39. XIA Xianfei, SUN Yu, WU Kai, et al. Wear mechanism of ring die for straw briquetting machine[J]. Ransactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(4): 32-39.

[13] 蒋清海，武凯，孙宇，等. 生物质制粒机环模的磨损机理分析[J]. 农业工程学报，2013 29(22)：42-49. JIANG Qinghai, WU Kai, SUN Yu, et al. Wear mechanism analysis of ring die of pellet mill[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(22): 42-49.

[14] 彭建云. 高效、节能挤压制粒成型技术研究[D]. 南京：南京理工大学，2013.

[15] 武凯，孙宇. 环模制粒成型技术与装备[M]. 北京：科学出版社, 2013.

[16] BINDUMADHAVAN G, SEVILLE J P K, ADAMS M J, et al. Roll compaction of a pharmaceutical excipient: experimental validation of rolling theory for granular solids[J]. Chemical Engineering Science, 2005,60:3891-3897.

[17] STEFANIE P, LAMMENS R F, STEFFENS K J. Roller compaction/dry granulation: use of the thin layer model for predicting densities and forces during roller compaction[J]. Powder Technology, 2010,199:165-175.

[18] 吴劲锋，黄建龙. 苜蓿草粉制粒密度与挤出力模拟试验[J]. 农业机械学报，2007, 38 (1)：68-71. WU Jinfeng, HUANG Jianlong. Simulated experiment and model of pelletizing density and extruding force for alfalfa powder[J]. Transaction of Chinese Society for Agricultural Machinery, 2007, 38(1): 68-71.

[19] 彭建军. 秸秆颗粒燃料冷态压缩成型实验研究及数值模拟[D]. 大连：大连理工大学，2008.

[20] DIARRA H, MAZEL V, BOILLON A, et al. Finite element method (FEM) modeling of the powder compaction of cosmetic products: comparison between simulated and experimental results[J]. Powder Technology, 2012, 224: 233-240.

[21] SINHA T, BHARADWAJ R, CURTIS J S, et al. Finite element annalysis of pharmaceutical tablet compaction using a density dependent material plasticity model[J]. Powder Technology, 2010, 202: 46-54.

[22] HAN L H, ELLIOTT J A, BENTHAM A C, et al. A modified drucker-prager cap model for die compaction simulation of pharmaceutical powders[J]. International Journal of Solids and Structures, 2008,45: 3088-3106.

[23] DEC R T, ZAVALIANGOS A, CUNNINGHAM J C. Comparison of various modeling methods for analysis of powder compaction in roller press[J]. Powder Technology, 2003,130:265-271.

[24] KUMAR D, DIXIT U S. A slab method study of strain hardening and friction effects in cold foil rolling process[J]. Journal of Materials Processing Technology, 2006,171: 331-340.

[25] LI F, PAN J, SINKA I C. Contact laws between solid particles[J]. Journal of the Mechanics and Physics of Solids,2009,57: 1194-1208.

[26] WU C Y, COCKS A C F. Numerical and experimental investigations of the flow of powder into a confined space[J]. Mechanics of Materials, 2006,38: 304-324.

[27] 曹康，金征宇. 现代饲料加工技术[M]. 上海：上海科学技术文献出版社, 2003.

[28] 高永毅, 焦群英, 唐果，等. 等截面梁纯弯曲振动的几何非线性分析[J].振动与冲击，2003, 22(1)：72-74. WU Yongyi，JIAO Qunying, TANG Guo, et al. Nonlinear bending vibration analysis of uniform beam[J]. Journal of Vibration and Shock, 2003, 22(1): 72-74.

[29] 崔圣爱，祝兵. 客运专线大跨连续梁桥车桥耦合振动仿真分析[J].西南交通大学学报，2009, 44 (1)：66-71. CUI Sheng’ai，ZHU Bing. Modeling and analysis on extruding force in pelleting process[J]. Journal of Southwest Jiaotong University, 2009, 44(1): 66-71.

[30] 陈明，马吉胜，高岩. 有限段法在自动武器多体动力学分析中的应用[J]. 振动与冲击，2008,27(7)：158-160. CHEN Ming, MA Jisheng, GAO Yan. Application of finite segment method in the mutil-body dynamics of automatic weapon[J].Journal of Vibration and Shock, 2008, 27(7): 158-160.

Vibration analysis and structural optimization of a ring die pellet mill with rotor eccentricity

SHEN Jiangfei, WU Kai, CUI Xian’an, SUN Yu

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Ring die pellet mills have been widely used in the biomass-energy, feed industry, chemical industry because ring die pellet mills have a series of advantages, such as a high forming rate, lower pollution, energy-efficient and etc. However, the existing ring die pellet mills have serious vibration issue, especially for the pellet mills with rotor eccentricity. The vibration of ring dies severely shortens the ring die life. According to the powder pressure-density relationship and the pressure distribution in deformation area, the accurate interaction force between rollers and ring dies was figured out with considering the positive static frictional force on the roller surface. The change law of the interaction force between the roller and the ring die with relative displacement was also discussed. A dynamic simulation model of ring die pellet mills with rotor eccentricity was set up by using the multi-body software. Dynamic simulations were performed to study the vibration of revolving shaft, dead axle, and compaction force. The results reveal that the interaction force between the roller and the ring die varies linearly with the relative displacement between the roller and the ring die. The revolving shaft support segment of the dead axle should be stouter than the frame support segment. Increasing the dead axle diameter will lead to reduced vibration of the revolving shaft but increased compaction force. A flexible bar was used to fix rollers to the dead axle to solve the problem. The simulation shows that the optimization can dramatically reduce the vibration of the compaction force. The radial stiffness of frames should be kept above 1×107N/m. The bending rigidity of frames should be kept above 1×105N·m/deg. There is an optimum value for the bearing spacing parameter at different stiffness of bearings of the revolving shaft.

ring die pellet mill; rotor eccentricity; dynamic simulation; powder compaction; vibration

江苏省自然科学基金项目(BK2011706)；江苏省产学研联合创新资金-前瞻性联合研究项目(BY2012023)

2015-04-29 修改稿收到日期：2015-10-13

沈江飞 男，硕士生，1991年7月生

武凯 男，博士，教授，1972年8月生

TH113

A

10.13465/j.cnki.jvs.2016.24.010