基于自由振动衰减响应的硬涂层材料力学特性参数辨识

孙 伟， 王 茁

(东北大学 机械工程与自动化学院，沈阳 110819)

基于自由振动衰减响应的硬涂层材料力学特性参数辨识

孙 伟， 王 茁

(东北大学 机械工程与自动化学院，沈阳 110819)

获得硬涂层材料的储能模量和损耗因子等力学特性参数是硬涂层复合结构建模及减振优化设计的基础。现有的关于硬涂层材料参数辨识研究通常是基于梁形试件和复杂的实验过程。而这里面向悬臂板结构，提出一种仅需测得涂层前后悬臂板的时域共振自由振动衰减响应，来辨识硬涂层材料力学特性参数的方法。首先，确定了由自由振动衰减响应辨识硬涂层储能模量及损耗因子的原理。进一步，给出了获得上述硬涂层材料参数所需的关键参数(包括响应包络线、即时共振频率和阻尼)的辨识方法。再则，描述了硬涂层板有限元建模以及共振频率、模态应变能和参考应变的求解方法。最后以涂敷NiCoCrAlY+YSZ硬涂层的悬臂薄板为例进行了实例研究，获得了该混合涂层的储能模量及损耗因子。进一步，将获得的硬涂层材料参数代入到有限元分析模型，通过对比试验与有限元计算获得的硬涂层板前6阶共振频率，证明了所辨识的材料参数的合理性。经比较发现，辨识获得的硬涂层储能模量及损耗因子随参考应变的变化规律同其他文献基本一致，但该结果可直接用于硬涂层板形结构的建模。

自由振动衰减响应；硬涂层；力学特性参数；参数辨识

硬涂层是指由金属基、陶瓷基或两者的混合制成的涂层材料，目前主要用于热障、抗摩擦和抗腐蚀。近年来的研究发现，硬涂层可以在高温、高腐蚀环境下降低薄壳构件的振动应力，因而硬涂层阻尼减振研究受到了越来越广泛关注[1-3]。进一步的研究发现，硬涂层之所以能减振是源于硬涂层颗粒之间的内摩擦，TASSINI[4]，TORVIK[5],AL-RUB[6]等分别创建了微观材料学表征模型来解释硬涂层的减振机理。为了更好地实施硬涂层阻尼减振，还需要创建宏观的硬涂层复合结构的动力学分析模型，基于该分析模型来实现对硬涂层减振性能的有效预估与设计。而创建这样的模型的关键是获得硬涂层材料，诸如储能模量(杨氏模量)、损耗因子等力学特性参数。

大量的研究[7-9]已经发现硬涂层材料具有应变依赖性。所谓的应变依赖性实质上是一种对强迫振动响应幅度的依赖性，用于表征结构响应幅度的可以是振动位移、振动速度、振动加速度，当然也包括应变响应幅度，且目前已经习惯于用应变响应幅度来表征。在应变依赖性的影响下，硬涂层的储能模量、损耗因子会随着复合结构的应变响应幅度发生改变。硬涂层材料的应变依赖特性，也会使涂敷硬涂层的复合结构表现出变刚度、变阻尼的非线性振动特性。此外，硬涂层材料还具有受涂敷工艺影响明显的特点，即同一种硬涂层材料，在不同制备工艺下，会表现出不同的力学特性参数。例如，PATSIAS等[10]分别测试了由等离子喷涂(APS)和电子束物理气相沉积(EBPVD) 制备的同一种涂层的力学特性参数，结果发现两者有很大的不同。可见，硬涂层材料的上述特点致使辨识硬涂层材料力学特性参数具有很大的挑战性和迫切性。

针对硬涂层材料力学特性参数辨识需求，目前学者已提出多种方法，总体上可分为三种，分别为压痕法[11]、弯曲测试法[12]、振动测试法[7-9,13]等。由于仪器设备简单、操作方便，基于振动测试的辨识方法得到了广泛的应用。在振动测试法中，应用较为广泛的是基于Oberst beam理论的辨识技术，美国材料协会(American Society of Testing Materials，ASTM)[13]已将此项技术作为辨识涂层材料参数的一项基本技术。PATSIAS等[7]采用了Oberst beam 法进行了辨识硬涂层材料力学特性参数的实践，通过测试悬臂梁试件的涂层前后的振动特性参数，获得了硬涂层具有幅度依赖性的储能模量和损耗因子。另一种基于振动法的测试技术其辨识原理同样来自于梁理论，TORVIK[9]分别推导了涂层前后悬臂梁的储能和耗能规律，并将具有应变依赖性的涂层参数用多项式表达，进而实现了考虑应变依赖性的硬涂层力学特性参数的辨识。

上述针对硬涂层材料参数的辨识主要针对涂层梁结构，为了获得硬涂层材料参数，需要测试不同激励幅度下涂层前后梁的振动特性参数，实验工作量大且引入测试误差的环节增多。由于处于共振状态结构的自由振动衰减响应包含了即时响应、即时共振频率、阻尼等大量信息。因而本文面向悬臂板结构，提出一种仅需测得涂层前后悬臂板的共振时域自由振动衰减响应，来辨识硬涂层材料力学特性参数的方法。首先确定了由自由振动衰减响应辨识硬涂层储能模量及损耗因子的原理；进一步给出了获得硬涂层材料参数所需的关键参数(例如响应包络线、即时共振频率、阻尼等)的辨识方法；再则描述了硬涂层板有限元建模以及共振频率、模态应变能和参考应变的求解方法；最后以涂敷NiCoCrAlY+YSZ硬涂层的悬臂薄板为例进行了实例研究，获得了该混合涂层的储能模量及损耗因子，并简要证明了所辨识的硬涂层材料参数的合理性。

1 辨识原理

具有应变依赖性的硬涂层材料参数可定义为

(1)

如果将硬涂层涂敷在已知材料参数的金属基体上，当切断处于共振状态复合结构的激励源时，可测试结构件上某点的自由振动衰减响应。该自由振动衰减响应中含有大量的信息，具体包括：①从自由振动衰减响应中可获得包络线，描述的是不同的位移响应幅度；②从自由振动衰减响应中可获得随时间变化的结构的即时共振频率(或者称之为时变共振频率)；③从自由振动衰减响应中可获得复合结构的阻尼，而且是一个时变的阻尼。这些信息通过恰当的处理则可以描述硬涂层材料的应变依赖性。以下说明硬涂层储能模量及损耗因子的辨识原理。

1.1 硬涂层储能模量的辨识原理

在薄板由共振状态开始的自由振动衰减过程中，随着响应幅度的减少，硬涂层的储能模量会发生改变。进一步，硬涂层材料储能模量的改变也会使整个复合板共振频率发生变化。如果可以通过分析模型来捕捉该频率的变化，并将分析结果与实测值进行比对，则可反推出随应变变化的储能模量值。相应的，面向薄板自由振动衰减响应的硬涂层储能模量的辨识流程可用图1来描述。

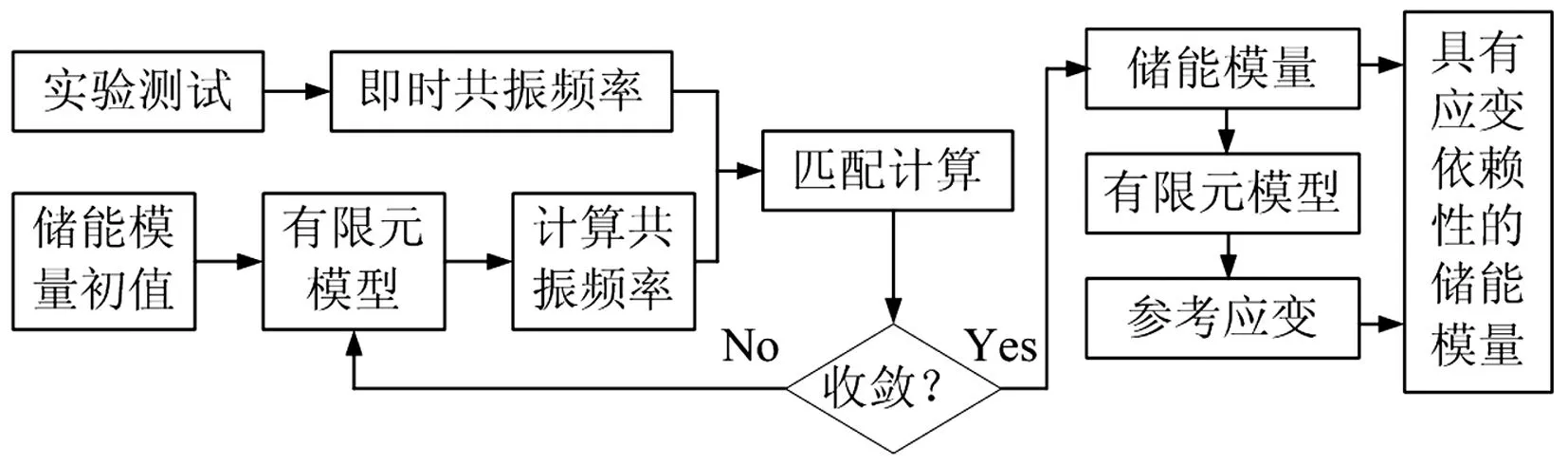
图1 硬涂层储能模量的辨识流程Fig.1 The procedure of identifying storage modulus of hard coating

图1所示的是基于反推法辨识硬涂层储能模量的流程。其基本思想是不断地修正储能模量值以使计算获得的共振频率与实测的即时共振频率相一致，进而反推出硬涂层材料的储能模量。由自由振动衰减数据获得的即时共振频率是一系列的离散点值，可选择其中一部分将用于辨识硬涂层的储能模量，关于即时共振频率的辨识详见第2部分。这里用有限元法作为工具计算硬涂层复合结构的共振频率及用于表征应变依赖性的参考应变，详见第3部分。

基于反推法辨识的核心是匹配计算，需要涉及模型修正技术[14]使理论分析的结果快速收敛于实验值，进而反推出所辨识的硬涂层材料参数。基于模型修正技术的匹配计算原理如下：

设硬涂层的储能模量EcR为模型修正技术中的设计变量。硬涂层复合板的第n阶特征值λn对该设计变量的灵敏度SE,n，可表示为

(2)

式中，灵敏度采用差分法获得，其设计变量变化量即步长ΔEcR设为10-4×EcR。φn为复合板的第n阶模态振型，K和M分别为复合板的刚度及质量矩阵。

而特征值与共振频率的关系，可表示为

λn=(2πfn)2

(3)

式中：fn为复合板的第n阶即时共振频率，单位为Hz。

模型修正技术的目标函数可按如下最小二乘原理来定义，即

Δλn=SE,nΔEcR

(4)

式中:Δλn为第n阶特征值变化量，ΔEcR为储能模量的变化量。在保证即时共振频率得到修正的同时，要求设计变量的变化量尽可能的小，则最终的目标函数可描述为

(5)

相应的迭代公式为

(6)

式中:WE为储能模量的修正加权系数。WE取0～0.3，设计变量不灵敏时需取高值，同时高的WE也意味着迭代次数需增加。由于振动衰减仅针对某一阶次，可设置较高的精度。后续实例设收敛条件为修正后的计算共振频率与相应的实验值偏差在0.001%，经过若干次迭代，则可获得对应于某一应变响应幅度下的储能模量。

1.2 硬涂层的损耗因子辨识原理

硬涂层的损耗因子同样具有应变依赖性，即在薄板由共振状态开始的自由振动衰减过程中，硬涂层的损耗因子也会随着响应幅度的减少而发生改变。基于自由振动衰减响应辨识硬涂层损耗因子的流程可用图2来描述。

图2 硬涂层损耗因子的辨识流程Fig.2 The procedure of identifying loss factor of hard coating

同样，关于由自由振动衰减响应辨识涂层前后薄板损耗因子的方法参见第2部分，而关于基于有限元模型求解应变能和参考应变详见第3部分。

在图2所示的流程中，硬涂层损耗因子辨识计算公式是基于对涂层复合结构的储能及耗能分析获得的[15]，具体为

(7)

式中：η为涂层后薄板的损耗因子，ηs为涂层前板的损耗因子，RSE为硬涂层与基体的应变能比。可见，将不同响应幅度下涂层前/后损耗因子和对应的模态应变能比代入式(7)，进一步获取对应的参考应变，则可求得具有应变依赖性的硬涂层损耗因子。

2 基于自由振动衰减响应的时变参数辨识

为了获取硬涂层的力学特性参数，需要由硬涂层复合结构的自由振动衰减响应中获取包络线、即时共振频率、阻尼等。以下详细说明上述参数的提取方法。通常，结构的时域自由振动衰减响应中包含有大量的噪音，在上述参数辨识之前，还需进行降噪处理。这里采用十阶巴特沃斯(Butterworth)带通滤波器对时域振动衰减响应进行降噪处理。

2.1 提取包络线

获得的包络线是后续阻尼辨识以及参考应变计算的重要依据。由于硬涂层复合板的自由振动衰减响应是一个非线性时变信号，这里采用分段处理。将原始信号分成若干时间段Δt，每段可近似为线性信号，并采用希尔伯特(Hilbert)变换来提取每个时间段对应的自由振动衰减响应的包络线。

设对应于每个时间段，降噪后的衰减信号可表示为

(8)

式中：A为初始位移，ζn和ωn分别为第n阶即时模态阻尼比和即时共振圆频率。

对信号进行希尔伯特变换处理，有

(9)

(10)

2.2 即时共振频率辨识

由希尔伯特变换所获得的分析信号，可得到自由衰减信号的即时相位φ(t)，求解式为

(11)

进一步，由即时相位就可获得硬涂层板的即时共振频率ωn(t)，求解式为

(12)

需要说明的是上述即时共振频率的求解同样也是针对各时间段内的数据而进行的。最终经差分处理，则可获得每个时间段Δt内近似为常值的共振频率。

2.3 阻尼辨识

由图2所示的辨识流程可知，阻尼辨识需同时针对同一阶次的涂层前后薄板共振状态的自由振动衰减数据，但两者在辨识方法上是一致的。这里利用获得的包络线数据来辨识薄板系统的阻尼(用模态损耗因子来描述)。考虑到损耗因子的时变性，对应于每个时间段的数据采用如下公式进行辨识

(13)

(14)式中：X1，X2为包络线上时间间隔为Δt两点处的响应值。这样处理后对应每个时间段的损耗因子也为常值。

这种针对时域自由振动衰减响应分段处理的参数辨识方法，即可以很好地描述硬涂层材料的应变依赖特性，又可以最大限度的减少噪音对辨识结果的干扰。通过以上处理就获得了各时间段Δt对应的包络线、即时共振频率、阻尼等参数。每个时间段Δt对应的数据可作为具有应依赖性的硬涂层材料参数辨识的一个数据点。

3 薄板固有特性及参考应变计算

这里，选用ANSYS软件，按照有限元法对涂层薄板结构进行动力学建模及分析。参照图1和图2所示的流程可知，有限元计算的内容包括共振频率计算、模态应变能计算和参考应变计算。计算的结果用于辨识具有应变依赖性的硬涂层材料参数，计算的次数与所选用的时间段数量相等。另外，上述计算的顺序也不能改变，因为后一个计算要基于前一个计算的结果。以下简要说明相关计算方法。

共振频率的计算主要用于辨识硬涂层的储能模量，为了考虑阻尼的影响，做了如下修正

(15)

式中：fupdated和fFEM分别为修正的共振频率和有限元模态计算获得的共振频率，ζn通常为模态损耗因子的1/2。参照后续的实验结果可知涂敷硬涂层后复合板的模态损耗因子小于0.01，因而实际上fupdated和fFEM的结果相差不大。

按照设定的优化模型，需要进行一系列的迭代计算使计算获得的共振频率与试验中每个时间段确定的即时共振频率差值最小，从而反推出储能模量值。

参照式(7)可知，模态应变能的计算主要用于获得硬涂层及基体的应变能比RSE，相应的计算式为

(16)

式中：Kc，Ks分别为涂层与基体的刚度矩阵。在ANSYS中，可以直接在后处理中提取上述应变能。同样针对每一个储能模量值，都要进行一次模态应变能计算，相关结果用于硬涂层损耗因子的辨识。

在复合结构的某一响应幅度下，通常选择硬涂层和基体结合面处的最大应变来作为参考应变描述硬涂层能材料的应变依赖特性。由于本文的研究对象为薄板结构，单独选择任意方向的应变作为参考应变是不科学的，需要选择等效应变来作为描述硬涂层应变依赖性的参考应变。薄板结构等效参考应变εe可按照应变能密度相等的原则来定义，具体为

σeεe=σxεx+σyεy+τxyγxy

(17)

式中:σx,σy和εx,εy分别为x及y方向的正应力及正应变，τxy和γxy分别为xy平面内的剪应力和剪应变，σe为等效应力。参考应变的计算仍旧与各时间段的辨识或分析数据相对应，具体方法可描述为：将辨识获得的储能模量及复合结构损耗因子代入有限元模型；施加激励并调整激励幅度值直到分析与实测的自由振动衰减响应幅度近似一致为止；参见模态振型，获得最大应变的位置；提取该最大应变处的等效应变即为该自由振动衰减响应幅度对应的参考应变。

4 研究实例

这里以涂敷NiCoCrAlY+YSZ硬涂层的悬臂薄板为例来演示本文所研发的算法。

4.1 测试试验件及实验系统

涂敷NiCoCrAlY+YSZ硬涂层前后的钛板见图3。该薄板的长、宽分别为153.1 mm，109.6 mm，钛板基体的厚度为1.44 m。在薄板的一侧涂敷硬涂层，涂层厚度为0.3 mm。薄板夹持区长度为20 mm。钛板的材料参数是已知的，具体为：储能模量110.32 GPa，密度4 420 kg/m3，损耗因子0.000 7。硬涂层的密度可由实测获得具体为5 600 kg/m3，硬涂层及钛板的泊松比均取0.3，硬涂层的其他材料参数，包括储能模量和损耗因子则需要辨识获得。

图3 钛板实验件Fig.3 Titanium test pieces

这里采用振动台基础激励，在获得涂层前后薄板共振点的前提下，用共振频率激励来获得涂层前后薄板的自由振动衰减响应。实验现场见图4，所涉及的仪器设备见表1。用激光测振仪拾振，参见图4中的坐标，拾振点为x=29 mm，y=41 mm。表1中的PCB模态力锤主要用于测试涂层板前6阶共振频率，相应的结果用于后续校验所辨识的硬涂层材料参数的合理性。

图4 硬涂层板基础激励测试Fig.4 The test of hard-coating plate under base excitation

序号名称1LMS16通道便携式数据采集前端控制器2PolytecPDV-100激光多普勒测振仪3LMS.Testlab笔记本工作站4KINGDESIGNEM-1000F振动台5PCB8206-00154627模态力锤

4.2 硬涂层力学特性参数辨识

这里以涂层前后悬臂板的第6阶为对象，由第6阶共振自由振动衰减响应辨识具有应变依赖性硬涂层的力学特性辨识。在4 g激励幅度下，首先由扫频三维瀑布图获得涂层前后薄板的共振频率分别为，1 297 Hz(涂层前)，1 259.13 Hz(涂层后)。进一步分别用共振频率激励涂层前后的薄板，待响应稳定后停止激励，进而就可以获得涂层前后薄板的时域共振衰减响应。

以下仅以涂层后的薄板为例，说明数据处理过程。选用十阶巴特沃斯带通滤波器，频率范围设置为1 259.5～1 261.5 Hz对自由振动衰减信号进行降噪处理，并用希尔伯特变换提取包络线，降噪信号及包络线见图5。为了有效辨识，这里选择0～0.1 s的数据，每间隔0.05 s非连续地取出10个时间段用来进行即时共振频率及损耗因子的辨识。需要说明的是在本实例中，包络线辨识所选用的时间段数量远大于上述值，覆盖了整个自由振动衰减的时间范围(见图5)。接下来，针对每个时间段的数据，用差分法求得的即时频率，按式(13)和式(14)求得损耗因子。最终，对应各时间段，经上述操作获得了用于辨识硬涂层材料力学特性参数所需的所有参数。相关结果均列在表2中，具体包括涂层板的即时共振频率、位移响应、损耗因子以及未涂层板的损耗因子。此外还需说明的是由于实测的是速度响应v，这里利用v/ωn将其转化为位移响应。

创建硬涂层板的有限元模型，见图6。在该有限元模型中，基体及涂层板均采用SHELL281单元，在整个模型中共有800个单元， 2 562个节点。基于这个有限元模型进行匹配迭代计算，就可以获得对应上述10个时间段的硬涂层储能模量。接着，将获得的硬涂层储能模量重新输入有限元模型中，按式(16)获得硬涂层及基体的模态应变能比。进一步分别将上述应变能比以及表2中涂层前后损耗因子代入式(7)，则可获得对应上述各时间段的硬涂层的损耗因子。最后，分别将获得的储能模量及复合板损耗因子输入有限元模型，参照各时间段的位移响应，按第3部分所描述的方法就可以确定对应各位移响应的参考应变。上述所有辨识结果均列在表3中。由表3可知，这里获得的硬涂层材料参数的应变依赖性不强，这是由于激励能量(或者激励幅度)较小所造成的。

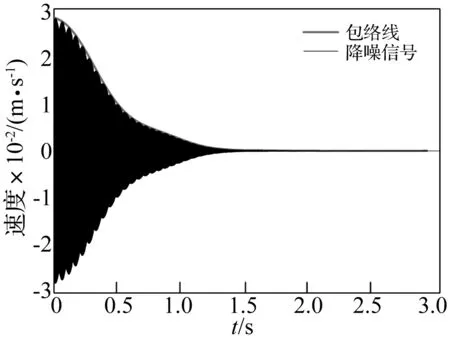
图5 涂层板第6阶共振自由振动衰减信号及包络线Fig.5 Free decay signal and envelop of coated plate for the 6th order resonance

参照表3，以参考应变为横轴，分别以硬涂层储能模量及损耗因子为纵轴，则可以确定具有应变依赖性的力学特性参数，相关结果见图7。由图7可知，辨识获得的硬涂层储能模量随参考应变的增大而减小，而损耗因子则随参考应变先增大再减小，上述变化规律同其他文献结果基本一致。只是本文是针对硬涂层悬臂板结构，而其他文献均是针对梁型试件。考虑到硬涂层力学特性参数随工艺变化明显这一特点，如果需针对硬涂层板形结构进行建模，本文所辨识的结果可以被直接应用。

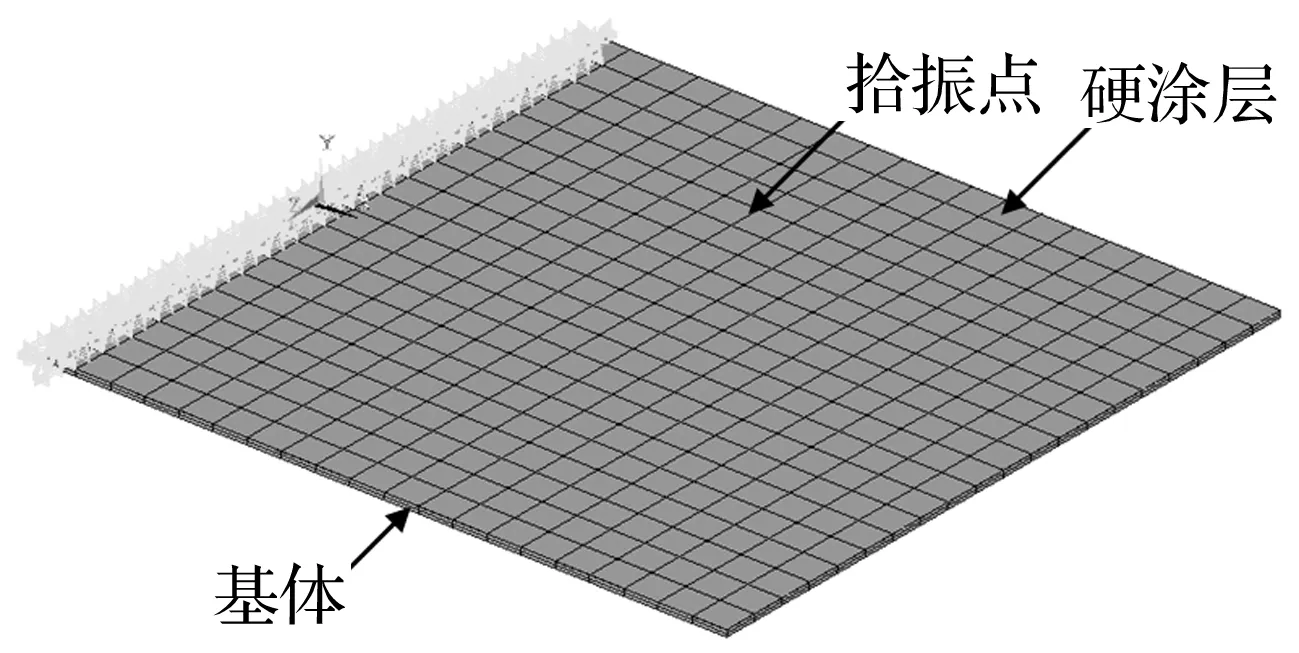
图6 硬涂层悬臂板有限元模型Fig.6 FE model of hard-coating cantilever plate

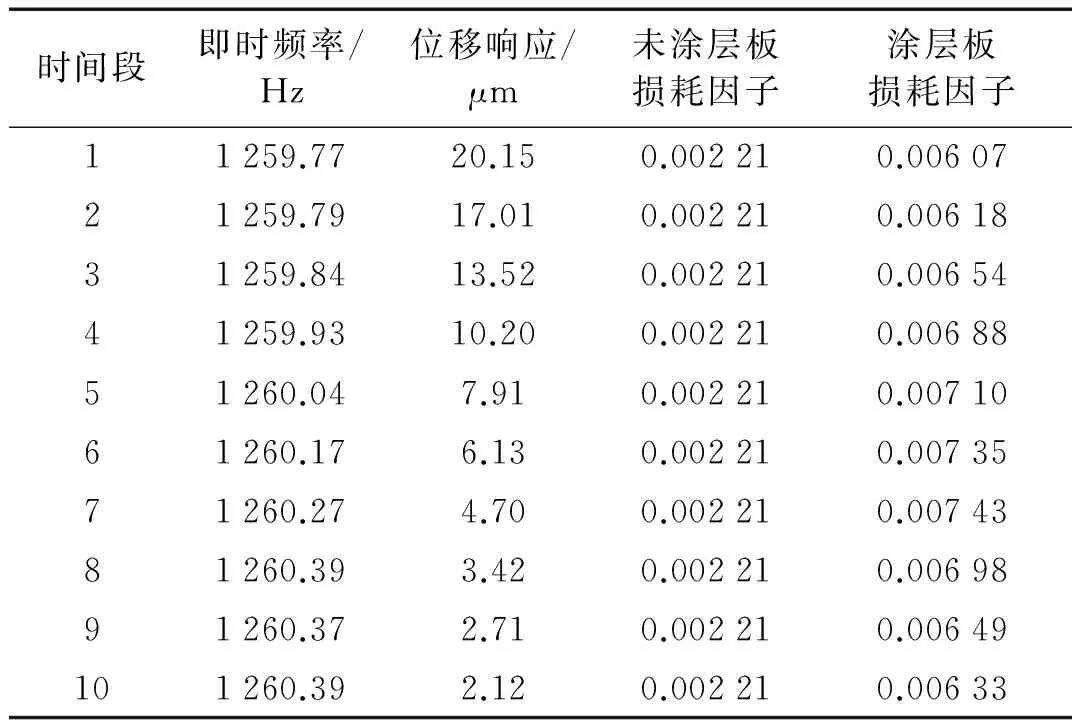
时间段即时频率/Hz位移响应/μm未涂层板损耗因子涂层板损耗因子11259.7720.150.002210.0060721259.7917.010.002210.0061831259.8413.520.002210.0065441259.9310.200.002210.0068851260.047.910.002210.0071061260.176.130.002210.0073571260.274.700.002210.0074381260.393.420.002210.0069891260.372.710.002210.00649101260.392.120.002210.00633

表3 硬涂层力学特性参数辨识结果Tab.3 Identification results of mechanical parameters of hard coating

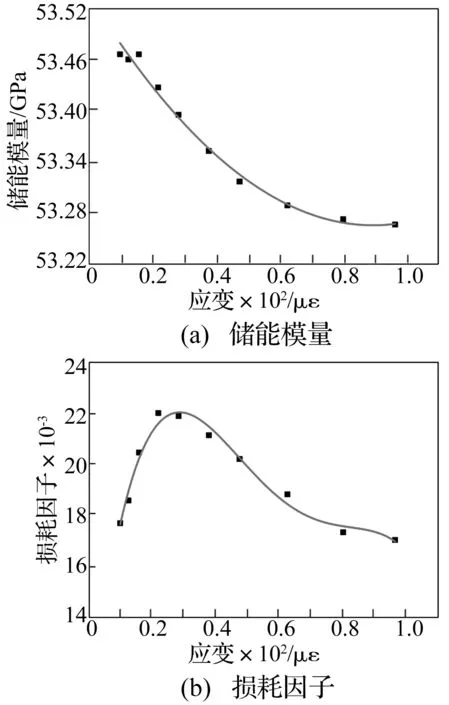
图7 硬涂层力学特性参数的应变依赖性表征Fig.7 Characterization of hard-coating mechanical parameters with strain dependent characteristics

4.3 辨识的硬涂层参数合理性验证

为了证明所辨识的硬涂层参数的合理性，以下将辨识的硬涂层材料参数代入到所创建的硬涂层板有限元模型中，计算前6阶共振频率。同时利用锤击法测试涂层板的前6阶共振频率，在锤击测试中拾振点与图4一致，敲击位置在薄板的右侧边缘。计算结果、测试的结果以及两者的比较均列在表4中。需要说明的是考虑到所辨识的硬涂层材料参数应变依赖性不强，因而这里仅取时间段1对应的材料数据，进行有限元计算，因而这是一种粗略的计算。由表4可知，用针对第6阶共振自由振动衰减响应辨识得到硬涂层材料参数计算获得的硬涂层板前6阶共振频率与锤击法实测的结果基本一致，因而可以说明这里所辨识的硬涂层材料参数具有合理性。

5 结 论

获得硬涂层材料的储能模量和损耗因子等力学特性参数，对于硬涂层复合结构建模及阻尼减振优化设计都有重要的意义。本文研发了从涂层前后薄板结构共振状态下的自由振动衰减响应来辨识上述硬涂层材料力学特性参数的方法，得出以下结论。

(1)研究的实践表明，基于涂层前后薄板共振状态下的自由振动衰减响应，采用反推法并利用匹配计算可获得硬涂层的储能模量，利用涂层前后结构件的储能及耗能规律公式，可确定硬涂层的损耗因子。

(2)相对于现有的、需要多个激励幅度测试的硬涂层材料力学特性参数的辨识方法，本文所研发的方法实验量较少。只需测得某一激励幅度下涂层前后薄板同一阶次的共振状态自由振动衰减响应就可实现硬涂层参数的有效辨识。

(3)本文提出对时域自由振动衰减响应分段处理的参数辨识方法。这样做的好处是一方面可以很好地描述硬涂层材料的应变依赖特性，另一方面可以最大限度的减少噪音对辨识结果的干扰。

(4)将获得的硬涂层材料参数代入到有限元分析模型，通过对比试验与有限元计算获得的硬涂层板前6阶共振频率，发现两者结果基本一致。此外，发现本文辨识获得的硬涂层储能模量及损耗因子随参考应变幅度变化的规律同其他相关文献结果也是基本一致。从而证明了本文所辨识的硬涂层材料参数的合理性。这里针对的是硬涂层悬臂板结构，而其他文献均是针对梁形试件。考虑到硬涂层力学特性参数随工艺变化明显这一特点，如果需针对硬涂层板形结构进行建模，本文所辨识的结果可以被更加直接地应用。

[1] BLACKWELL C, PALAZOTTO A, GEORGE T J, et al. The evaluation of the damping characteristics of a hard coating on titanium[J]. Shock and Vibration, 2007,14(1): 37-51.

[2] IVANCIC F, PALAZOTTO A. Experimental considerations for determining the damping coefficients of hard coatings[J]. Journal of Aerospace Engineering,2005,18(1):8-17.

[3] 孙伟，齐飞 ，韩清凯. 基于自由振动衰减信号包络线法辨识硬涂层复合结构的阻尼特性[J]. 振动与冲击，2013,32(12)：50-54. SUN Wei, QI Fei, HAN Qingkai. Estimating system damping for a hard coating composite structure based on envelope of a free damped vibration signal[J]. Journal of Vibration and Shock, 2013,32(12)：50-54.

[4] TASSINI N, PATSIAS S, LAMBRINOU K. Ceramic coatings: a phenomenological modeling for damping behavior related to microstructural features[J]. Materials Science and Engineering: A, 2006, 442(1): 509-513.

[5] TORVIK P J. A slip damping model for plasma sprayed ceramics[J]. Journal of Applied Mechanics, 2009, 76(6): 061018.

[6] AL-RUB R K A, PALAZOTTO A N. Micromechanical theoretical and computational modeling of energy dissipation due to nonlinear vibration of hard ceramic coatings with microstructural recursive faults[J]. International Journal of Solids and Structures, 2010, 47(16): 2131-2142.

[7] PATSIAS S, SAXTON C, SHIPTON M. Hard damping coatings: an experimental procedure for extraction of damping characteristics and modulus of elasticity[J]. Materials Science and Engineering: A, 2004, 370(1): 412-416.

[8] TASSINI N, LAMBRINOU K, MIRCEA I, et al. Study of the amplitude-dependent mechanical behaviour of yttria-stabilised zirconia thermal barrier coatings[J]. Journal of the European Ceramic Society, 2007, 27(2): 1487-1491.

[9] TORVIK P J. Determination of mechanical properties of non-linear coatings from measurements with coated beams[J]. International Journal of Solids and Structures, 2009, 46(5): 1066-1077.

[10] PATSIAS S, TASSINI N, LAMBRINOU K. Ceramic coatings: effect of deposition method on damping and modulus of elasticity for yttria-stabilized zirconia[J]. Materials Science and Engineering: A, 2006, 442(1): 504-508.

[11] WEI P J, LIN J F. A new method developed to evaluate both the hardness and elastic modulus of a coating-substrate system [J]. Surface & Coatings Technology, 2005, 200(7): 2489-2496.

[12] KIM H J, KWEON Y G. Elastic modulus of plasma-sprayed coatings determined by indentation and bend tests [J]. Thin Solid Films,1999, 342(1/2):201-206.

[13] ASTM International. ASTME756-04 standard test method for measuring vibration-damping properties of materials[S]. 2005.

[14] MOTTERSHEAD J E, LINK M, FRISWELL M I. The sensitivity method in finite element model updating: a tutorial[J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2275-2296.

[15] 孙伟，贾师，刘营. 硬涂层悬臂梁减振机理分析模型的建立[J]. 东北大学学报(自然科学版)，2015, 36(5): 695-698. SUN Wei, JIA Shi, LIU Ying. Establishment of model of damping mechanism for the hard-coating cantilever beam[J]. Journal of Northeastern University(Natural Science), 2015, 36(5): 695-698.

Identification of the mechanical parameters of hard coating based on free vibration decay response

SUN Wei, WANG Zhuo

(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)

Obtaining the mechanical parameters of hard coating is the premise of modeling and damping design of a hard-coating composite structure. Most studies about identifying the mechanical parameters of hard coating are based on beam specimen and a complex test procedure. Here, a cantilever thin plate structure was considered. A new identification method was presented, which only needed to test the free vibration decay responses from resonance status for the uncoated and coated plate. Firstly, based on the free vibration decay responses, the principles of identifying storage modulus and loss factor of hard coating were proposed. Then, to effectively obtain the mechanical parameters of hard coating, the method of identifying some key parameters (such as envelop of response, instant resonance frequency and damping) was given. Next, the FEM modeling of hard-coating plate and solution of resonance frequency, modal strain energy and reference strain were described. Finally, the cantilever thin plate coated NiCoCrAlY+YSZ hard coating was chosen to demonstrate the proposed method. The storage and loss factor of this mixing coating were identified. Furthermore, the obtained material parameters were inputted into the created FEM model and the rationality of identified parameters was proved by comparing the first 6 orders resonance frequency obtained by measurement and FEM calculation respectively. The identification results show the change rules of storage modulus and loss factor of hard coating with the strain amplitude are consistent with the results listed in other similar references. However, the results herein can more directly serve for the dynamic modeling of hard-coating plate-shape composite structures.

free vibration decay response; hard coating; mechanical parameters; identification of parameters

国家自然科学基金资助项目(51375079)

2015-07-02 修改稿收到日期：2015-11-16

孙伟 男，博士，副教授，1975年生

TB535

A

10.13465/j.cnki.jvs.2016.24.024