基于准瞬态发动机模型的车辆传动系统特性分析

吴虎威， 吴光强,2

(1.同济大学 汽车学院，上海 201804； 2.东京大学 生产技术研究所，东京 153-8505)

基于准瞬态发动机模型的车辆传动系统特性分析

吴虎威1， 吴光强1,2

(1.同济大学 汽车学院，上海 201804； 2.东京大学 生产技术研究所，东京 153-8505)

研究了怠速工况下车辆传动系统动力学特性和机械变速器齿轮敲击建模方法，并通过实车实验验证了研究方法的有效性。首先，利用实车装备的直列四缸四冲程发动机特性参数，建立了考虑动态摩擦扭矩特性的准瞬态发动机模型；其次，利用集中质量建模方法，建立怠速工况下车辆动力传动系统动力学模型，模型中详细建立机械变速器空套齿轮阻滞力矩模型，仿真分析了传动系统各部件的运动特性和齿轮对敲击强度。最后，利用实车怠速工况下的实验结果，验证了准瞬态发动机模型和车辆动力传动系统仿真模型的有效性，研究成果可进一步用于车辆动力传动系统设计开发和变速器齿轮敲击产生机理研究。

齿轮敲击；准瞬态发动机模型；阻滞力矩模型；实车实验

汽车动力传动系统振动噪声作为车辆振动噪声的重要来源，其品质直接影响车辆乘坐舒适性。随着车用发动机向小型化、低转速方向发展，发动机产生的较大扭矩波动会激起动力传动系统较剧烈的扭转振动，尤其是对于装备机械式手动变速器的车辆，容易引起变速器齿轮敲击现象。齿轮敲击噪声因其特殊的宽频噪声特性而区别于其他噪声，易使乘员感到烦躁不安以及误以为变速器出现系统故障，从而引起的顾客抱怨越来越多。因此，针对车辆动力传动系统动力学特性研究和变速器齿轮敲击建模方法研究显得尤为重要。

目前针对车辆动力传动系统特性研究和变速器齿轮敲击建模方法的研究已有很多。TSUJIUCHI等[1]建立了怠速工况下车辆动力传动系统模型，探究了离合器扭转减振器第一级迟滞扭矩对齿轮对敲击特性的影响规律。BILE等[2]针对怠速工况下的某款五挡手动变速器建模，仿真分析了不同敲击被动齿轮转动惯量、齿侧间隙和啮合刚度对于敲击强度的影响规律，但模型中简化认为敲击被动齿轮阻滞力矩为零，这与实际情况差别较大。项小雷等[3]针对某款双中间轴式手动变速器，细化变速器内每对齿轮模型，将动力传动系统扭振运动作为非承载齿轮敲击模型的激励，再现发生敲击现象时各挡位齿轮的敲击形式，但非承载齿轮敲击模型中只是单一引入一定的黏性阻尼而考虑阻滞力矩。ROBINETTE等[4]利用基于集中质量的建模方法，针对某款五挡手动变速器建模，模型中对于敲击被动齿轮阻滞力矩进行详细建模，并且利用试验验证了阻滞力矩模型的工程实用性[5]，可借鉴用于本论文的建模研究，但传动系统模型中的动力扭矩输入认为是随时间等幅值增加的，这与发动机模型不符。发动机激励是作为动力传动系统的输入，其有效建模是研究的重要环节。发动机扭矩包括指示扭矩(包括质量扭矩和气体扭矩)和摩擦扭矩，其中指示扭矩建模已经成熟，部分简化模型中认为发动机扭转周期内摩擦为恒定值，与实际相比误差较大，摩擦扭矩建模一直是发动机建模的研究热点。RAKOPOULOS等[6]较早认识到发动机动态摩擦模型在发动机建模中的重要性，模型中考虑活塞与气缸体摩擦、活塞裙部摩擦和曲轴主轴承摩擦模型等，并利用试验进行了验证，成果可用于建立有效的动态发动机模型。

本文综合国内外研究成果和不足，考虑发动机动态扭矩输入，建立考虑摩擦扭矩特性的准瞬态发动机模型。利用集中质量建模方法，建立怠速工况下车辆动力传动系统动力学模型，仿真分析了传动系统各部件运动特性和变速器齿轮敲击强度。利用对应的实车实验结果验证了准瞬态发动机模型和车辆动力传动系统扭转振动模型的有效性。

1 准瞬态发动机模型

发动机模型，根据能否反映720°曲轴转角内运动状态及输出力矩的波动情况，分为稳态模型和瞬态模型。在发动机瞬态模型建模中，直接以发动机燃烧过程产生的缸内压力示功图作为输入的得到的发动机模型，称为准瞬态发动机模型。准瞬态发动机模型，包括指示扭矩模型和动态摩擦模型。

1.1 单缸发动机指示扭矩模型

针对单缸四冲程发动机进行指示扭矩建模，指示扭矩包括气体扭矩和往复质量惯性扭矩。

1.1.1 曲柄连杆机构运动学分析

曲柄连杆结构的运动学关系如图1所示，根据图中的运动学关系求得曲轴转角α与活塞位移sk的关系:

(1)

λp=r/l

(2)

式中，r为曲柄半径；l为连杆长度；

假定此时曲轴角速度ω为常值，即：

α=ωt

(3)

(4)

(5)

图1 曲柄连杆机构运动学关系图Fig.1 Kinematic diagram of the crank and connecting rod mechanism

1.1.2 曲柄连杆机构受力及力矩分析

曲柄连杆机构的受力关系如图2所示，其中对于图中受力Fε，有：

图2 曲柄连杆机构受力分析图Fig.2 Stress analysis diagram of the crank and connecting rod mechanism

(6)

(7)

(8)

式中，Fg为气体压强作用活塞力；Pg为气缸内气体燃烧压力；dp为活塞直径；FI为活塞、活塞环、活塞销及部分连杆的等效质量往复惯性力；mp为活塞、活塞环、活塞销及部分连杆的等效质量。

对应作用在曲柄上的扭矩大小为

(9)

(10)

式中，Tg为单缸四冲程发动机气体扭矩；TI为往复质量惯性力矩。

实验测得发动机怠速工况下的缸内气体压强随曲轴转角α变化曲线如图3所示，对应的Tg、TI和指示扭矩Tg+TI随曲轴转角变化关系如图4所示。由图4可知，在发动机处于怠速工况下，转速很低，在曲轴转过720°过程中，往复质量惯性力矩作用相对于气体扭矩作用小，指示扭矩与气体扭矩大小基本保持一致。

图3 怠速工况下气缸内气体压力图Fig.3 Cylinder gas pressure diagram in idle speed

图4 气体扭矩、惯性扭矩和指示扭矩变化图Fig.4 Gas torque, inertia torque and indicated torque changing diagram

1.2 单缸发动机摩擦模型

在发动机低负荷运行过程中，机械摩擦损耗相对于输出扭矩而言不能忽略，准确描述发动机的摩擦特性对瞬态发动机建模的至关重要。本文采用应用最为广泛的RH摩擦模型，RH摩擦模型将发动机摩擦扭矩分为活塞环黏性摩擦力矩Tf1、活塞环混合摩擦力矩Tf2、活塞裙部摩擦力矩Tf3、气门组摩擦力矩Tf4、附件摩擦力矩Tf5和主轴承摩擦力矩Tf6，各摩擦力矩分别定义为[7]

(11)

(12)

(13)

(14)

Tf5=c5μω

(15)

(16)

(17)

式中，ci(i=1,2,…,6)为发动机各摩擦扭矩拟合系数；μ为润滑油动力黏度；Pr为活塞环与缸壁接触压力；wo为油环厚度；d为气缸内壁直径；no为油环个数；nc为气环个数；wc为气环厚度；ho为润滑油膜厚度；Ls为活塞裙部长度；nv为单气缸内气门个数；Fs为气门弹簧力；rjb为轴颈轴承平均半径。

发动机总摩擦扭矩Tf大小为

Tf=Tf1+Tf2+Tf3+Tf4+Tf5+Tf6

(18)

当发动机处于怠速工况，利用720°曲轴转角周期内的瞬态测量结果进行辨识各摩擦扭矩拟合系数ci(i=1,2,…,6)，得到的单缸四冲程发动机在怠速工况下的发动机摩擦扭矩如图5所示(与图3对应)。

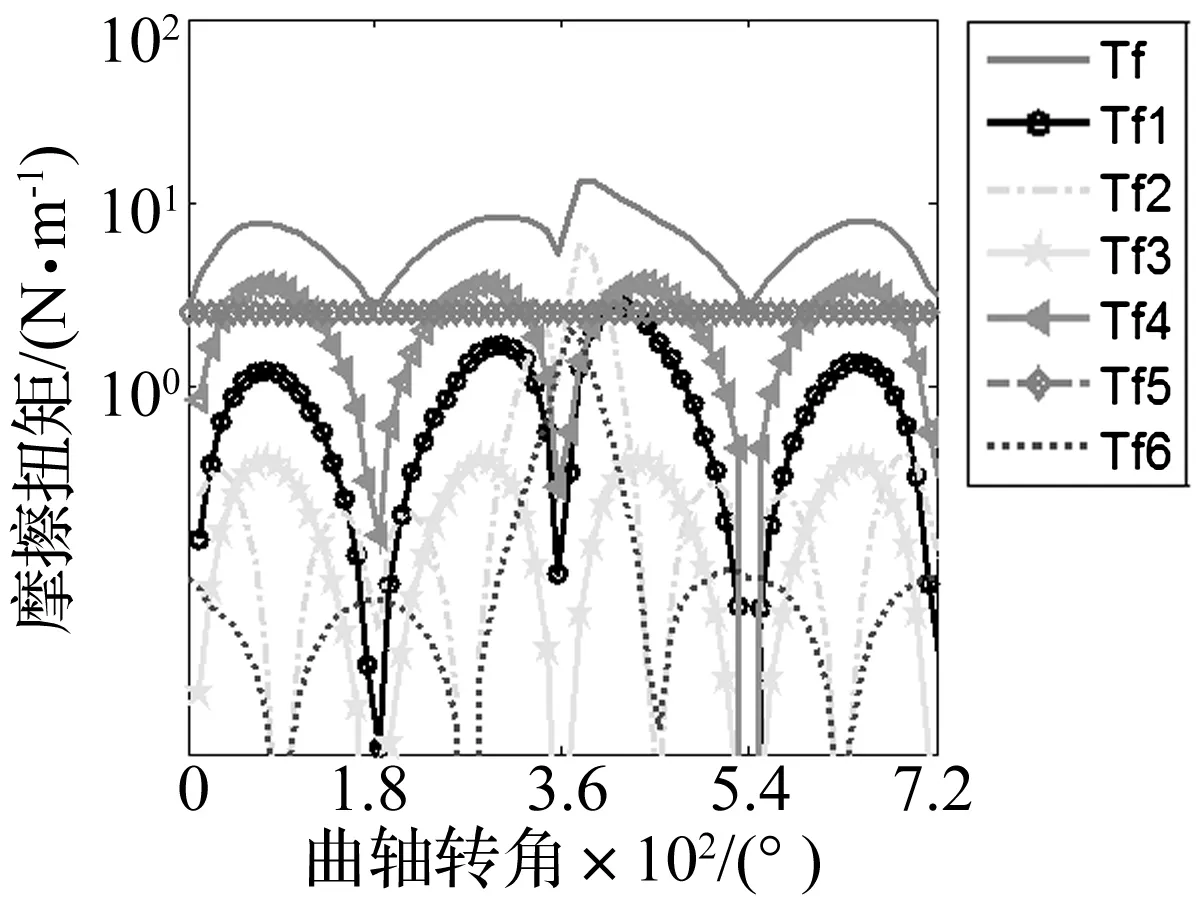
图5 基于RH摩擦模型的各摩擦扭矩图Fig.5 Frictional torque based on RH frictional model

1.3 四缸四冲程发动机有效输出力矩

发动机在运转过程中受到气体力矩、往复质量惯性力矩和摩擦力矩综合作用。考虑到直列四缸四冲程发动机四缸之间的相位角关系，发动机有效输出力矩Te大小为

(19)

该直列四缸四冲程发动机模型参数如表1中所示，此时得到该发动机怠速工况下的有效输出扭矩、指示扭矩和摩擦扭矩如图6所示(与图3对应)。

图6 四缸四冲程发动机输出力矩Fig.6 Output torque of a four-cylinder and four-stroke engine

参数数值参数数值r/m0.04d/m0.084l/m0.14ho/mm0.002dp/m0.08Ls/m0.15wo/m0.006rjb/m0.058wc/m0.004Pr/kPa20Fs/N300no2mp/kg0.4nc3μ/(kg·ms-1)0.015nv2c121c20.16c30.04c41.5c51.8c60.06

2 汽车怠速工况动力传动系统建模

2.1 车辆动力传动系统建模

实车装备的五挡手动变速器，其结构如图7所示。当发动机处于怠速工况时，离合器处于接合状态，变速器置于空挡，车辆和变速器输出轴静止不动，一挡、二挡输入轴齿轮带动相应输出轴空套齿轮一起转动，而变速器其他挡位齿轮出于静止状态。

当发动机处于怠速工况时，离合器扭转减振器工作于第一级刚度范围内。利用集中质量建模方法，等效的车辆动力传动系统动力学模型如图8所示(模型中忽略倒挡齿轮特性影响)。

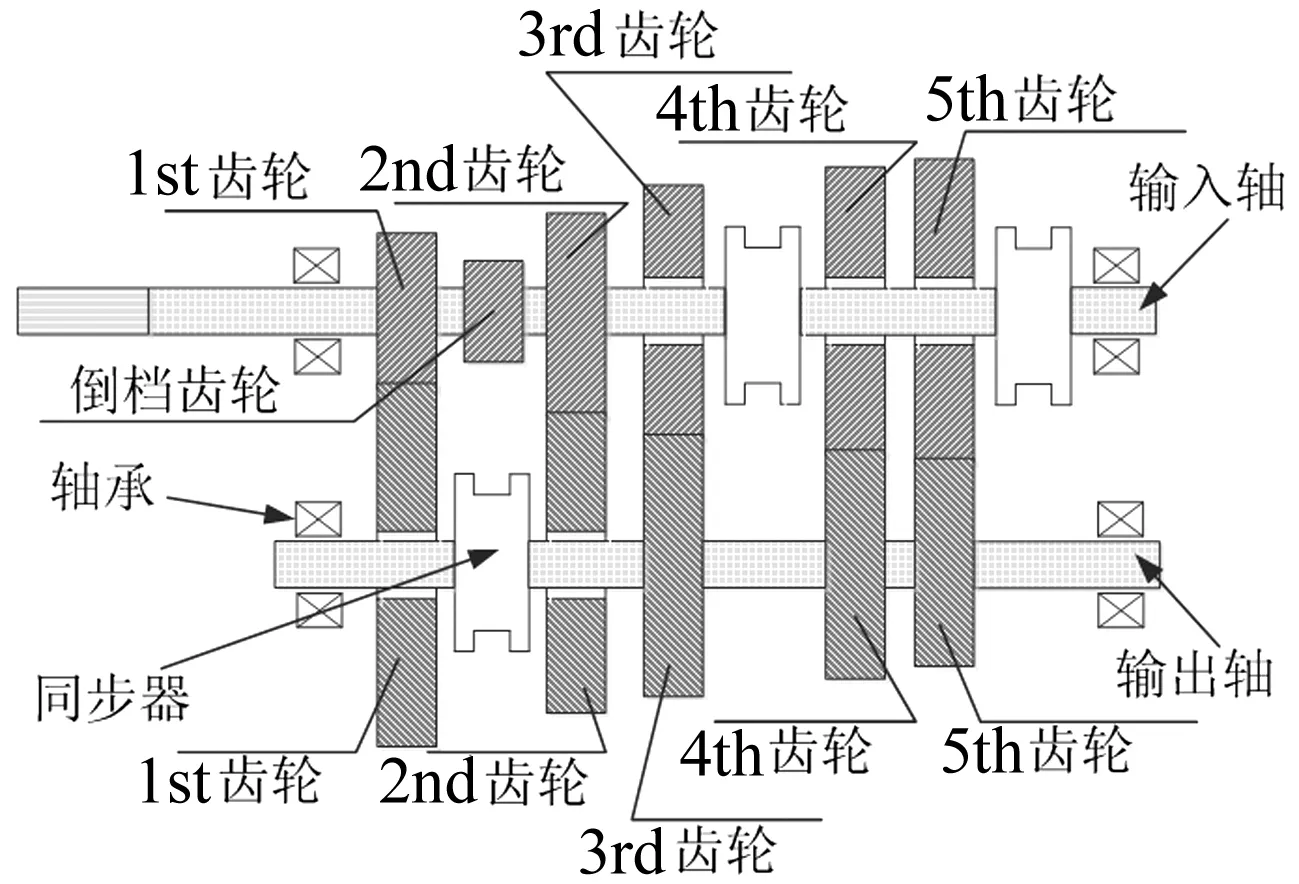
图7 五挡变速器结构简图Fig.7 5-speed transmission mechanism structure

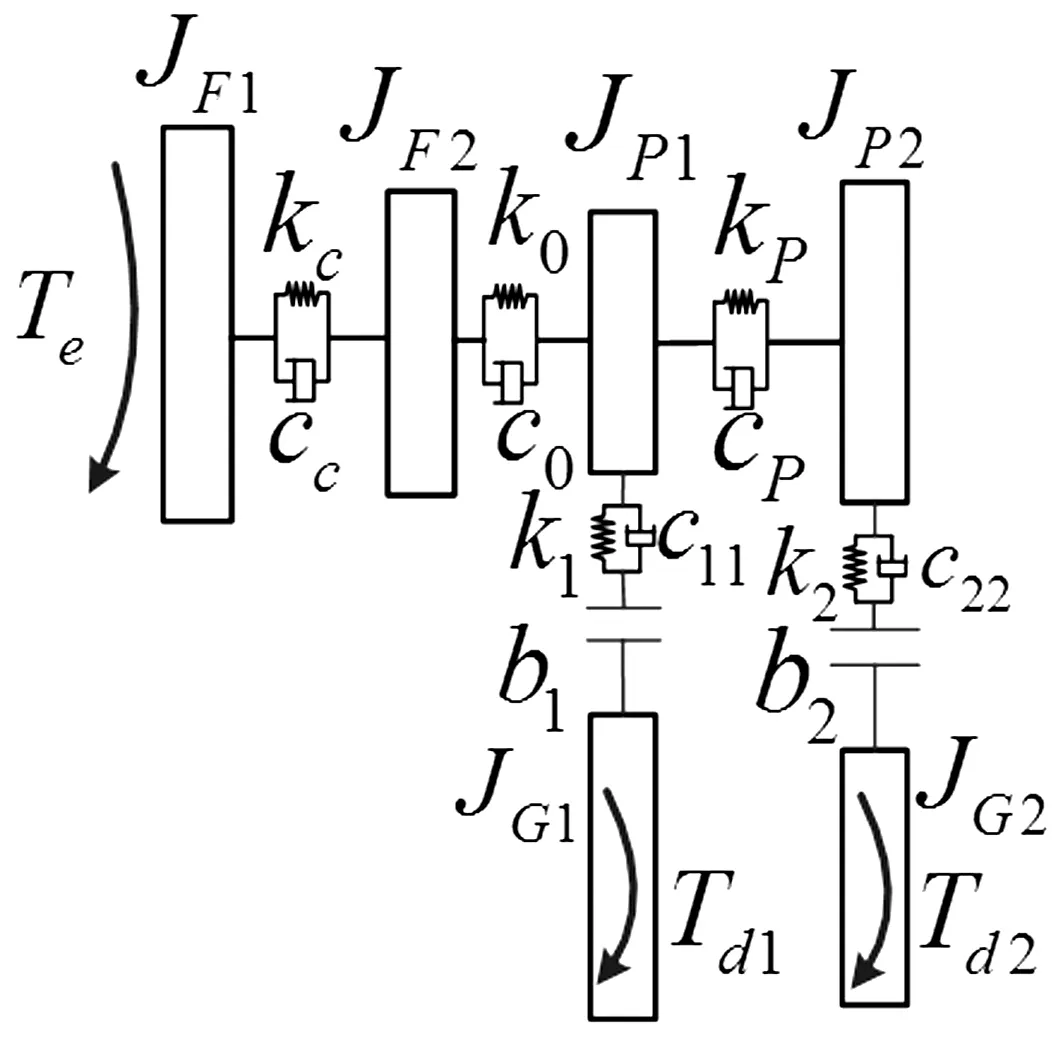
图8 怠速工况下的动力传动系统动力学模型Fig.8 Equivalent dynamic model of vehicle powertrain system on idle condition

根据牛顿第二定律，得到车辆动力传动系统扭转振动微分方程组为

(20)

式中，

J=[JF1JF2JP1JP2JG1JG2]T

θ=[θF1θF2θP1θP2θG1θG2]T

T=[Te0 0 0 -Td1-Td2]T

Tb=[0 0Tb1Tb3Tb2Tb4]T

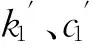
其中，Tbi(i=1,2,3,4) 为作用于各挡位齿轮的回复力矩(Restoring Torque)[8]，该回复力矩是由于考虑各挡位齿侧间隙大小而产生的非线性敲击力(矩)，各回复力矩大小分别为

(21)

(23)

X1=θP1RP1-θG1RG1

(25)

X2=θP2RP2-θG2RG2

(26)

式中，b1为一挡齿轮对齿侧间隙大小；b2为二挡齿轮对齿侧间隙大小。

该怠速工况下的车辆动力传动系统动力学模型中，各参数大小如表2中所示。

2.2 空套齿轮阻滞力矩建模

空套齿轮阻滞力矩模型参考文献[4-5]中的研究成果。当变速器处于空挡时，一、二挡输出轴空套齿轮受到轴承摩擦损失力矩Trb和轮齿搅油损失力矩Tch同时作用。

表2 车辆动力传动系统模型参数列表Tab.2 Parameters list of the vehicle powertrain system model

滚子轴承摩擦力矩Trb计算公式为

(27)

(28)

式中，N为轴承内、外圈相对转速；dm为轴承内、外圈平均直径；f0为润滑因子；ν为润滑油运动黏度。

齿轮搅油损失力矩Tch计算公式为

(29)

式中，ρ为润滑油密度；ωg为齿轮旋转角速度；Sm为齿轮浸油面积；R为齿轮节圆半径；Cm为搅油损失力矩系数。

一挡、二挡输出轴空套齿轮所受阻滞力矩大小分别为

Td1=Trb1+Tch1

(30)

Td2=Trb2+Tch2

(31)

2.3 齿轮对敲击力计算

齿轮对在齿侧间隙内产生敲击振动，而激起轮齿之间的敲击力。一挡、二挡齿轮对敲击力大小计算公式为

(32)

(33)

(34)

(35)

3 仿真结果分析

针对如图8所示的基于集中质量的动力传动系统动力学模型，进行车辆怠速工况下各部件运动仿真，结果如图9中所示。

由图9(a)可知，发动机转速在830 r/min上下波动，振动幅值大约为60 r/min；由图9(b)～图9(d)中结果可知，从动盘毂、输入轴一挡齿轮和输入轴二挡齿轮转速时域内变化基本保持一致，均在830 r/min上下波动，振幅大约为20 r/min；由图9(e)和图9(f)可知，输出轴一挡齿轮和输出轴二挡齿轮分别在240 r/min和425 r/min上下波动，时域内转速均存在突变，分别对比图9(g)和图9(h)中敲击力发生时刻，可知在转速突变处各齿轮对均发生了敲击现象；由图9(g)和图9(h)可知，一挡、二挡齿轮对在怠速工况下均发生轮齿敲击现象，各挡齿轮发生敲击的时刻不同，峰值均在200 N以内。

图9 时域内仿真结果Fig.9 Time-domain simulation results

为了验证离合器扭转减振器在动力传动系统中减振作用，需进一步分析发动机和从动盘毂转速时、频域结果。在时域内，发动机转速和从动盘毂转速对比结果如图10所示，发动机和从动盘毂均在830 r/min上下波动，从动盘毂转速振动幅值相对发动机转速振动幅值减小大约40 r/min。在频域内，由图11发动机转速频谱图可知，发动机转速在27.34 Hz、55.47 Hz、82.81 Hz和110.2 Hz(分别对应于发动机转频的2倍频、4倍频、6倍频和8倍频)处存在较大的峰值，并且幅值大小依次降低；由图12输入轴一挡齿轮转速频谱图可知，从动盘毂转速相对于发动机转速在27.34 Hz和55.47 Hz处幅值分别降低了20.58 r/min和4.28 r/min，而在82.81 Hz和110.2 Hz处幅值降至几乎为零。可见，在怠速工况下，离合器扭转减振器减振作用明显，尤其是降低发动机转频的偶数倍频处幅值大小。

图10 发动机和从动盘毂转速对比Fig.10 Comparison between engine speed and clutch hub speed

图11 发动机转速频谱图Fig.11 Engine speed spectrum

图12 从动盘毂转速频谱图Fig.12 Clutch hub speed spectrum

4 怠速工况实验研究

为了验证仿真模型的准确性，进行了装有如图7所示的五挡手动变速器的实车怠速工况实验。限于当前实验条件和转速传感器布置空间限制，目前只测量发动机转速和输入轴一挡齿轮转速，布置的两个转速传感器分别用于测量对应于图8模型中转动惯量JF1(发动机)与转动惯量JP1(输入轴一挡齿轮)的转速信号。

在车辆热车状态下，完全释放离合器踏板、油门踏板，当发动机转速稳定后开始采集数据，采集多组实验数据后并选取信噪比最高的一组数据，此时得到的发动机转速和输入轴一挡齿轮转速如图13所示。由图13可知，得到的转速信号中仍存在较强的干扰信号，有必要对于原始数据进行降噪处理。利用小波变换对于原始信号进行降噪处理，得到的结果如图14所示。由图14可知，发动机在830 r/min上下波动，振动幅值大约为60 r/min；输入轴一挡齿轮同样在830 r/min上下波动，振动幅值大约为20 r/min。可知，以上结果与文中建模仿真得到的结果(如图10所示)保持一致，而且图14(b)和图9中发动机转速和输入轴一挡齿轮转速在时域内运动规律一致。

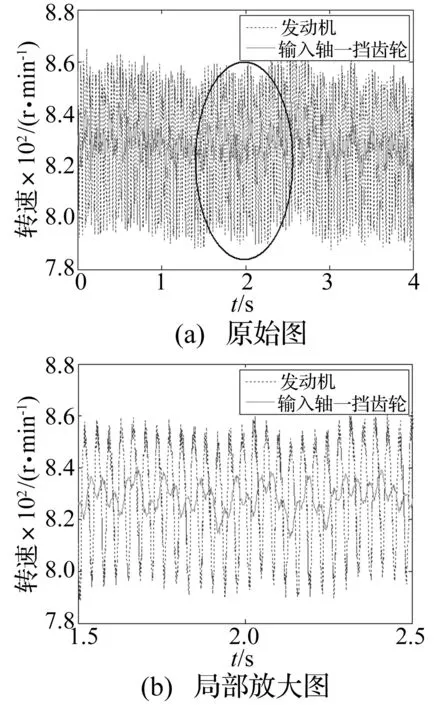
图13 试验测得原始数据Fig.13 Original experimental data

图14 小波变换降噪处理后试验数据Fig.14 Experimental data after noise reduction of wavelet transform

与建模仿真对应，通过实验验证离合器扭转减振器在动力传动系统中的减振作用。由图9仿真结果已知，从动盘毂和输入轴一挡齿轮在时域内的转速变化基本保持一致，因此只需分析发动机转速和输入轴一挡齿轮转速信号即可验证减振器作用。由图15发动机转速频谱图可知，在27.54 Hz、55.27 Hz、82.81 Hz和110.5 Hz处存在峰值，并且幅值大小依次降低，频率与幅值大小与图11中通过仿真得到的结果基本一致，峰值处对应的频率大小误差最大值为0.7%，因此仿真与试验结果误差均在合理范围内。由图16输入轴一挡齿轮转速频谱图可知，经过离合器扭转减振器减振作用后，一挡齿轮转速在27.54 Hz和55.27 Hz处的幅值相对于发动机转速对应频率处的幅值分别减小了19.93 r/min和5.35 r/min；经过减振作用后，输入轴一挡齿轮转速在82.81 Hz和110.5 Hz处幅值降至几乎为零，该结果与图12通过仿真得到的结果保持一致，峰值处对应的频率大小误差最大值为0.7%，因此仿真与试验结果误差均在合理范围内。经过实验结果可知，在怠速工况下，离合器扭转减振器对于降低发动机转速偶数倍频处幅值明显。

图15 发动机转速频谱图Fig.15 Engine speed spectrum

图16 输入轴一挡齿轮转速频谱图Fig.16 Input shaft 1st gear speed spectrum

5 结 论

(1)建立的更加准确、完善的准瞬态发动机模型，包括对发动机指示扭矩和动态摩擦扭矩的建模，本文利用建模仿真得到的发动机怠速工况下的传动系统各部件运动特性的时、频域结果，与实车实验结果具有很高的一致性。因此，基于准瞬态发动机模型得到的有效扭矩作为动力源，可提高汽车动力传动系统动力学模型的精确度和动态品质。

(2)详细考虑变速器空套齿轮阻滞力矩模型，包括

轴承摩擦损失力矩和齿轮搅油损失力矩，仿真结果可有效反映空套齿轮发生敲击作用时的运动形态，文中结果有待于进一步通过完善实验方案进行验证(如增加布置采集空套齿轮转速信号的传感器等)。

(3)本文针对车辆动力传动系统的研究方法和成果，可进一步用于车辆动力传动系统设计开发和变速器齿轮敲击产生机理研究。

[1] TSUJIUCHI N, KOIZUMI T, HARA N, et al. The effects of clutch damper in idling driveline rattle[M]//Topics in Nonlinear Dynamics, New York: Springer,2013: 259-267.

[2] BILE Y, GONDHALEKAR A, KUMBHAR M. Studies on neutral gear rattle in early stage design[C]// SAE Technical Paper, 2013.

[3] 项小雷, 陈德鑫, 李松松. 双中间轴式手动变速器齿轮敲击噪声理论及试验研究[J]. 汽车技术, 2014(11): 1-6. XIANG Xiaolei, CHEN Dexin, LI Songsong. Theoretical & experimental research of gear rattle noise of a double intermediate shaft manual transmission [J]. Automobile Science and Technology, 2014(11): 1-6.

[4] ROBINETTE D, BEIKMANN R S, PIORKOWSKI P, et al. Characterizing the onset of manual transmission gear rattle part II: analytical results[C]// SAE Technical Paper, 2009.

[5] ROBINETTE D, BEIKMANN R S, PIORKOWSHI P, et al. Characterizing the onset of manual transmission gear rattle part I: experimental results[C]// SAE Technical Paper, 2009.

[6] RAKOPOULOS C D, HOUNTALAS D T, KOUTROUBOUSIS A P, et al. Application and evaluation of a detailed friction model on a DI diesel engine with extremely high peak combustion pressures[C]// SAE Technical Paper, 2002.

[7] REZEKA S F, HENEIN N A. A new approach to evaluate instantaneous friction and its components in internal combustion engines[C]// SAE Technical Paper, 1984.

[8] WU G, LUAN W. The impact of gear meshing nonlinearities on the vehicle launch shudder[J]. SAE International Journal of Commercial Vehicles, 2015,8(1): 1-12.

Dynamic characteristics analysis of vehicle powertrain systems based on a quasi-transient engine model

WU Huwei1, WU Guangqiang1,2

(1. College of Automotive Studies, Tongji University, Shanghai 201804, China;2. Institute of Industrial Science, The University of Tokyo, Tokyo 153-8505, Japan)

Dynamic characteristics of vehicle powertrain systems and modeling methods of manual transmission gear rattle were studied under idle condition, which was then validated by vehicle experiment. Firstly, for an inline four-cylinder and four-stroke engine, a quasi-transient engine model considering dynamic friction property was built. Secondly, by the lumped mass modeling method, a dynamic model of the vehicle powertrain system on idle condition was established, taking into account loose gear drag torque. The model represented dynamic characteristics of powertrain systems and gear rattle phenomenon of manual transmission. Finally, effectiveness of the quasi-transient engine model and the vehicle powertrain system model was validated by vehicle experiment results on idle condition. The research achievements will contribute to vehicle powertrain system design and mechanism analysis of manual transmission gear rattle phenomenon.

gear rattle; quasi-transient engine model; drag torque model; vehicle experiment

国家自然科学基金(51175379)

2015-07-21 修改稿收到日期：2015-10-22

吴虎威 男，博士生，1987年生

吴光强 男，教授，博士生导师，1965年生

U463.2

A

10.13465/j.cnki.jvs.2016.24.028