有效渗透数学思想,提升学生思维能力
江苏省淮安市深圳路小学 王晶晶
有效渗透数学思想,提升学生思维能力
江苏省淮安市深圳路小学 王晶晶
数学思想是数学知识的核心和精髓,让学生掌握数学,可以帮助学生实现可持续发展。因此,在数学课堂中,教师不能单单传授给学生知识,还应该向学生逐步渗透知识背后的数学思想,掌握数学知识的本质,提升学生的数学素养,促进学生更好地发展。然而,学生对数学思想的领悟,并不是一朝一夕便能成功的,需要一个长期的、循序渐进的过程。所以在课堂教学过程中,教师应考虑小学生知识经验的局限性和数学思想的复杂性,有意识、有计划地渗透数学思想,让学生潜移默化地受到熏陶,提升思维能力,领略数学的魅力和神奇。
一、渗透转化思想,提升学生思维
转化,是数学的基本思想,在数学知识中有着很强的广泛性,向学生渗透数学思想无疑显得非常重要。加之,数学知识的系统性、逻辑性很强,前后的知识点有着非常密切的联系,借助于转化思想的应用,可以帮助学生突破新知学习,内化新知。所以,在数学课堂教学中,教师应注重渗透转化思想,帮助实现新知向旧知的迁移,帮助学生完成知识建构。
在教学平行四边形的面积时,教师首先借助方格图,在上面画了一个平行四边形,然后问学生这个平行四边形的面积是多少平方厘米(假定1格是1平方厘米)?学生运用数方格的方法,很快得出了方格图中平行四边形的面积。教师此时,像变魔术似的,隐去了方格图,出示了一个新的平行四边形,让学生猜一猜这个平行四边形的面积是多少平方厘米呢?学生以刚才那个平行四边形的面积为参照,有的说比刚才的平行四边形面积要大一些,也有的说比刚才的平行四边形的面积要小一些,而且两种意见争执不下,怎么解决呢?很快有学生提议,求出它的面积,问题便会迎刃而解。怎么求呢?教师让学生思考,能否借助以往学的知识解决这个问题呢?教师让学生拿出课前准备的平行四边形进行探究,学生们进行探索、讨论、交流,想到运用下面的方法去求平行四边形的面积,方法一:将平行四边形分成一个三角形和一个梯形,然后拼成长方形进行计算。方法二:将平行四边形分成两个梯形,然后拼成长方形。教师追问:这两种计算方法有什么共同点呢?学生们很快说出,都是将平行四边形转化成了长方形。教师进一步追问:“所拼长方形的长与宽,与原来平行四边形的底和高有什么关系呢?面积呢”学生们进入了新的探索中……
学生数学能力的提升需要我们教师在平时的教学中,不断引导,巧于点拨,转化思想,对于培养学生触类旁通,有效迁移的能力异常重要。上述案例,教师联系学生已有的知识基础,巧妙设疑,让学生主动迁移,将新知转化成了旧知,激发了学生的转化意识,提升了学生思维的灵活性。
二、渗透类比思想,深化学生思维
数学家波利亚说∶“类比是一个伟大的引路人。”其实,类比也是一种重要的数学思想,是在学习的过程中,引导学生把具有相似特点的知识点放在一起,进而让学生进行比较,得出异同点,掌握知识的本质特征。类比思想在数学课堂中的有效渗透,可以深化理解,把握本质,还可以培养学生的逻辑推理能力。
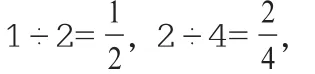
①分数的分子相当于除法运算中的什么?分数的分母相当于除法运算中的什么?
②能否用商不变规律,猜想一下分数有什么性质?
③想一想,分数的分子和分母可以同时乘或者除以0吗?为什么?
……
在课堂教学中,教师通过运用类比思想,让学生借助商不变规律,总结出了分数的基本性质,加深了学生对所学知识的理解。
学生只有学会比较发现,善于类比,才能在不同的知识点上找出相互之间的异同,从而经过积极思考,深化对知识的理解。上述案例,教师通过一道填空题,作为类比的引入点,通过问题层层铺垫,步步深入,让学生在类比中,加强了相关知识的联系,提升了课堂学习效果。
三、渗透数形结合思想,发展学生思维
数学知识抽象复杂,但学生由于认知能力的限制,遇到很多难度大一些的题目,往往不能准确理解题意,把握要领。这时,教师就可以引导学生将题目中抽象的数量关系,转变成直观、形象的图形,通过数形结合,降低学生解题时的难度,达到化繁为简、化难为易的目的。
在教学比例时,教师出示了这样一道题目:客车、货车的速度比是5:3,两车同时从A、B两地相对开出,在离中点120千米处两车相遇,货车行了多少千米?这道题目,如果让学生阅读文字后,就能列式解答,很有难度,而且解答的正确率也不会高。因为很多学生在做这道题目时,都会陷入这样的陷阱,认为客车比货车只多行了120千米,而画出线段图后,学生很容易理清数量关系,找到正确的解题方法:

线段图的直观性,使学生很快知道客车比货车只多行了2个120千米,这是解决问题的关键,下面列式解答就迎刃而解了。
数形结合的思想是学生数学学习中一种非常重要的思想,对于学生理解数学新知,提升数学素养具有重要意义,在小学阶段培养学生的数形结合思想,更对学生今后的数学学习奠定了良好的基础。上述案例,教师通过渗透数形结合的思想,将文字转化为图形,有效地化解了解题的难点,深化了学生的思维。
总之,数学知识是抽象的、系统的,而数学思想浓缩着数学知识的精华,蕴含着大智慧,应该让学生从小就开始接触、掌握数学思想。所以在课堂教学过程中,教师要注重渗透数学思想,更好地完善学生的认知结构,拓展学生的思维,彰显课堂教学的精彩。

