Banach格上Dunford-pettis算子的AM紧性研究

西藏大学理学院 孙文涛

Banach格上Dunford-pettis算子的AM紧性研究

西藏大学理学院 孙文涛

在Banach格上研究Dunford-pettis算子的AM紧性，对Dunford-pettis算子为AM紧性的一些条件进行探究，在现有的基础上已经得到了一些不错的成果。

Banach格；Dunford-Pettis算子；AM-紧性

一、引言

设定E与F属于Banach格，T：E→F属于有界线性算子，如果T把E当中的弱收敛于零集映为F中的相对紧集，那么T叫做Dunford-Pettis算子；如果T将E中序区间映为F中的相对紧集，那么T属于AM-紧算子；有关Dunford-Pettis算子和 AM-紧算子的性质和与其他特殊算子的联系，已经有了很深的探究。本文主要讨论了Banach格上Dunford-pettis算子的AM紧性研究。

二、Dunford-pettis算子的AM紧性

引理1.1 设定E属于Archimedean Riesz空间而且。V在E中序稠只有当对于随意u∈E＋，存在。当A输运E的理想时，A在E中稠只有当E属于A生成的带。

引理1.2 设定E，F属于Riesz空间并且F属于Dedekind完备。D属于Lb(e，f)的非空向上指标集。那么supD存在只有当随意集合有上界，那么成立：。

通过定理1.3 得知

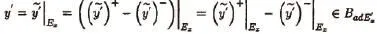
得证。

下列属于AM-空间，它的闭单位球是[-|x|，|x|]。

以下是Dunford-Pettis算子属于AM-紧算子的几个充分条件。

定 理1.5 设 定E、F属 于Banach格，T：E→F属 于Dunford-Pettis算子，那么以下条件之一成立时T属于AM-紧算子：（1）E拥有序连续范数；（2）对于随意，Ex离散；（3）E'离散；（4）F属于有限维空间。

证明：（1）E拥有序连续范数，那么E中任意区间都属于弱紧的，T是Dunford-Pettis算子，把任意有界集映为相对范数紧集，所以T属于AM-紧算子。

（2）T属于AM-紧算子只有当任意是紧算子。以下证明对于每个属于紧算子。事实上，对于属于AL空间，因此Ex拥有序连续范数。但是Ex离散，因此可得属于紧算子。

（4）由于T属于紧算子，所以属于AM-紧算子。

P.G.Dodds、D.H.Fremlin和J.Bourgain证明AL空间上的Dunford-Pettis算子构成一个带。Aliprantis和Burkinshaw做出以下推广：

定理1.6E属于Banach格并且有序连续范数，F属于AL空间，T： E →F属于正则算子，那么：

（1）T属于Dunford-Pettis算子只有当T属于AM-紧算子；

（2）Lb(E，F)中的Dunford-Pettis算子全体构成带。

以下为该定理成立的另一个条件：

定理1.7 设定E'属于离散的Banach格，F属于AL-空间。T：E→F为正则算子。那么

（1）T属于Dunford-Pettis算子只有当T属于AM-紧算子；

（2）Lb(E，F)中的Dunford-Pettis算子全体构成带。

证明：（1）必要性：根据定理1.6可得：

重复性：设定T把E中的序区间映成F中的范紧集，当E中弱收敛于零的序列{xn}，那么在弱拓朴σ（F，）下|Txn|→0。设定属于的单位元，那么，所以T属于Dunford-Pettis算子。

如果Banach格E中每个序列（xn)在弱拓朴σ（E，）下收敛于零可得序列（|xn|）在弱拓朴σ（E，）下收敛于零，那么叫做E中格运算弱序列连续。

定理1.8 设定E属于拥有单位元的AM-空间而且不离散，F不具有序连续范数，那么有非AM-紧的Dunford-Pettis算子S：E→F。

证明：只要证明S属于Dunford-Pettis算子。事实上，通过E是AM-空间，因此有弱序列连续的格运算。由于0≤S≤T且T属于Dunford-Pettis算子，因此S属于Dunford-Pettis算子，得证。

定理1.9 设定E属于Banach格且格运算弱序列连续，那么以下条件等价：

（1）对于每个Dedekind完备空间F，每个Dunford-Pettis算子T：E→F都是AM-紧算子；

（3）E'离散。

证明：“（1）→（2）”显然：

“（3）→（1）”由定理1.4可得。

三、总结

本文主要讨论了Banach格上Dunford-pettis算子的AM紧性研究，得到了一些有趣的结论，其中几个主要结果如下：

定理1.4：E属于Banach格而且E'离散。对于每个及，那么一定成立。

定理1.5 设定E、F属于Banach格，T：E→F属于Dunford-Pettis算子，那么以下条件之一成立时T属于AM-紧算子：

（1）E拥有序连续范数；（2）对于随意，Ex' 离散；（3）E'离散；（4）F属于有限维空间；

定理1.6E属于Banach格并且有序连续范数，F属于AL空间，T：E→F属于正则算子，那么：

（1）T属于Dunford-Pettis算子只有当T属于AM-紧算子；

（2）Lb(E，F)中的Dunford-Pettis算子全体构成带。

定理1.7 设定E '属于离散的Banach格，F属于AL-空间。T：E→F为正则算子。那么

（1）T属于Dunford-Pettis算子只有当T属于AM-紧算子；

（2）Lb(E，F)中的Dunford-Pettis算子全体构成带。

[1]韩霖，陈滋利，陈金喜. Banach格上O-Dunford-Pettis算子的共轭性质[J]. 西南民族大学学报(自然科学版)，2014（01）：83-86.

【论文受助项目：项目类型：西藏自治区自然基金项目；项目名称：序Dunford—Pettis算子的性质研究；项目编号：2015ZR-13-2】