例谈高中数学教学中学生思维障碍突破的策略
江苏省如皋市第一中学 侯飞建
例谈高中数学教学中学生思维障碍突破的策略
江苏省如皋市第一中学 侯飞建
高中数学对学生的数学思维提出了更高层次的要求,在数学教学中,教师不仅要关注到学生知识的掌握程度,也要帮助学生突破数学学习中常见的思维障碍,引导学生利用数学思维来处理数学问题。
思维障碍;高中数学;教学策略
数学思维障碍是指在数学问题变化中引起数学思维主体内部状态的紊乱和失调,并阻碍数学思维活动正常进行的主观体验。本文以高中数学教学实践为基础,探讨了数学教学中如何克服思维障碍,解决数学问题。
一、重视概念教学,避免数学思维断链
在数学教学中,学生思维障碍产生的很大一部分原因是对于概念的理解存在偏差,在教学中要加强对概念教学的重视,培养学生基本的数学思维形式,避免出现思维断链。如在进行指数函数一课的教学时,教学过程如下:
【概念产生】
情景1:据报告显示,从2000年开始的未来20年内,我国GDP年平均增长率可达到7.3%,x年后我国的GDP可以为2000年的多少倍?
情景2:某细胞分裂时有一定的规律,即每个细胞分裂成原来的两个,试写出分裂次数x和最终的细胞数目y之间的关系。
学生分析:上述情景中分别为y=1.023x(x∈N*,x≤20),y=2x(x∈N*,x>0)
设计目的:在学生学习数学概念的初期,对于概念理解还很陌生,以情景引入的方式将知识要素展现出来能够开拓学生思维。
【概念理解】
教师引导:观察上述两个式子,总结它们的特征。
学生活动:①两个式子都采用幂的形式来表示;②指数是自变量x;③底数大于0。
学生活动:如果a=1,那么该函数就成为一个常函数了;如果a=0,那么0的高次方也没有意义;如果a<0,那么当x为真分数时就不能取到对应的函数值。
设计目的:学生自己总结出指数函数的特征有助于后续理解。指数函数的定义域问题是学生在后续学习中容易产生思维障碍的出错点,在此进行深入探究能够帮助学生强化概念理解。
在概念学习的过程中,以情景引入的方式来弱化学生对于新知识的陌生感,同时强化学生在后续学习中容易出现思维障碍的知识点,以此来提高学生理解力。
二、强化变式思维,克服数学思维定式
学生在解决数学问题的过程中,很容易出现找不到解题思路的现象。教师通过变式例题,引导学生挖掘问题信息,解决数学问题,避免因找不到突破点而影响问题解决的现象。如在进行二次函数教学时,例题设计如下:
学生解决:进行配方后发现,对称轴x0=1在定义域内,最大值为4。
学生解决:该抛物线开口向下,但是由于a不确定,所以对称轴也不确定。当对称轴在定义域内时,函数最大值与对称轴有关;反之,最大值在定义域的边界点。得出结论:当a<-3时,最大值为;当-3≤a≤2时,;当a>2时,。
学生解决:由于a不确定,抛物线的开口不确定,但是对称轴为定值,因此只需要讨论抛物线开口即可。a>0,最大值在对称轴较远端取得为;a<0,最大值在对称轴取得为。
学生思考:在解决此问题时,由于思维定式,学生会按照变式2、3里的解决方法讨论,但是比较复杂。
教师引导:考虑最大值在何处取得。
学生思考:对于二次函数,最大值只能在对称轴或者端点处取得,因此分别考虑在x=-1.5,x=2,x=1/a-2处的函数值即可。
在解决此题的过程中,教师设计了三个变式对二次函数的最值进行探讨,在帮助学生形成数学思维的同时破除思维定势,以点带面使学生认识到问题的本质。
三、加强方法渗透,提高数学思维意识
数学方法的形成是克服思维障碍的有效方法,在教学的开展过程中,教师要注意在习题教学中渗透数学方法,提高学生利用数学思维解决数学问题的能力。如在进行下述题目的教学时:
要点1:两个对数的底不相同,如何进行转换(考查换底公式)。
要点2:如何避开log对参数进行求解(考查等价方程组的转化)。
要点3:如何对上式进行简化运算(考查三角函数的等价代换)。
此题目中虽然是对数函数的题目,但涉及的理论知识有对数换底公式、三角函数计算等,数学思想有等价方程组的代换、三角函数的等价代换、分类讨论等。通过解决此问题,学生的数学思维得到了提升,在面对此类问题时也避免了思维障碍的影响。
四、展现思维过程,促进数学思维形成
数学思维的培养是数学教学的重要目标之一,在教学的开展过程中,教师要注重展现思维的过程,鼓励学生从过程中发现数学规律,体会数学探究的乐趣,以数学思维的不断推进来避免思维障碍的产生。如在进行数列一课的教学时,设计题目如下:
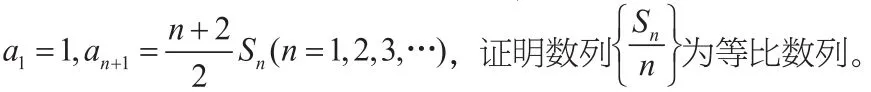
在解题过程中,教师展示了思维过程,培养了学生在解题中利用数学思维的习惯,克服了由于问题分割孤立形成的思维障碍。
数学思维障碍的突破给学生提供了一个新的起点,在开展教学时,教师要注意分析学生思维障碍产生的原因,采用适当的教学策略以突破学生的思维障碍,提高学习成果。

