循序渐进，高效复习相似三角形

江苏省盐城市亭湖新区实验学校 李 静

循序渐进，高效复习相似三角形

江苏省盐城市亭湖新区实验学校 李 静

相似三角形作为初中数学的重要知识点，是每年中考的必考点。相似三角形是全等三角形的拓展，学好相似三角形，不仅有助于对几何知识有更加深刻的认识，也巩固了全等三角形的知识，因此对相似三角形的复习是中考几何复习的重中之重。

初中数学；多元化；课堂教学

在传统的课堂中，教师是课堂的主人，学生只需被动的接受。因此，直接导入教学、教师全程讲解、学生疯狂记笔记等现象司空见惯，这样往往会使复习变得低效。由于相似三角形的知识点较多，且易与其他知识点相结合，常以此来构建压轴题。因此，在课堂教学中要注重循序渐进，促进高效复习。

一、经典例题讲解，发现漏洞

在复习相似三角形前，为了能让学生发现自身的不足，从而为接下来的复习明确目标、提高复习效率，可以讲解一些例题，让学生在做例题、讲例题的过程中，体会到哪些知识点已经遗忘，哪些知识点不熟悉。

一开始，我在屏幕上给出两道例题：

1.如图所示，DE=40cm，EF=20cm，AC=1.5cm，CD=8cm,求树高；

2.如图所示，D、E、F分别是△ABC三边的中点，，BC=a，AC=b，AB=c，△BDG∽△DFG，求证。

当例题给出时，我给学生几分钟的时间思考，然后请两位同学到黑板上尝试着解答此题，并要求其他学生在课堂笔记上试着解答问题。当大部分学生都完成的差不多时，我进行讲解。第一题主要考查的是相似三角形的判定和相似性质。由题干条件的两个垂直和一对公共角，即可得三角形相似，然后运用性质：对应边成比例，即可解出答案。在本题中需要注意的是单位的统一。第二题考查的知识点不仅是相似，还有中位线定理、圆周角定律。由和BD=CD，可得，由D、E、F分别是三边的中点，利用中位线定理可得DE∥AB，由FG=BG-BF得FG=FD，即可得△DFG为等腰三角形。因为△BDG∽△DFG，所以△BDG是等腰三角形，可得CD=BD=DG，由圆周角定律可得B、G、C三点共圆，即得。当例题讲解完后，我给学生5分钟左右的时间，让其寻找自己的薄弱之处。

经过对这些例题的分析和讲解，不仅可以让学生知道如何去解答问题，还可以让老师了解到学生在哪些地方存在漏洞，从而为接下来的知识讲解制定方案，这样可以有效地避免在复习过程中做无用功，提高了复习效率。

二、重难点讲解，修复漏洞

当学生发现自己的不足时，为了修复知识漏洞，让学生对知识体系有更加深刻的理解，应对本章节的重难点进行剖析和讲解。由于本阶段是对理论知识的讲解，为了使课堂气氛不枯燥无味，可以尝试让学生讲解、教师做适当的点拨和补充。

通过上一阶段的学习，学生了解到了一些不足之处，于是我请几位学生说一下他的不足之处有哪些。我总结了学生的不足之处，然后将学生分成几个小组，每个小组一个问题，要求每个小组的成员之间认真讨论如何通过讲解知识点弥补这些漏洞。此时我会做出提示，在讲解要认真分析一下知识点，也要尽量总结出其对应的常出现的题型。当学生讨论好后，我请每个小组派出一位代表进行讲解。在学生讲解时，如若学生讲解出现错误或不完整，我做出适当的点拨和补充。在学生讲解完后，我做出总结：（1）在运用相似三角形的比例性质时，要特别注重对应边，不能找错对应边；（2）要熟记一些相似三角形的基本图，如“A型”、“X型”等；（3）进行相似三角形的判定时，不能只看图，要根据条件进行判定。

学生在经过重难点的讲解后，对知识点有了一个系统的理解，对重难点及易错点也有了一个很好的认知。此外通过让学生分析、讲解和总结知识，让学生做课堂的主人，充分给予其展示的机会，这样不仅可以让学生的学习兴趣得到提高，也极大地调动了学生的主观能动性。

三、经典考题练习，进益求精

学生在经过系统的复习，完善不足之处后，可以布置一些经典的中考题供学生练习，一方面可以让学生体会一下中考题的难度，了解在中考中是如何考查该章节的知识点的，另一方面也有助于学生巩固知识，夯实基础。

由于数学知识点比较抽象，从而导致学生在实际应用中比较困难。通过以习题的方式来展开训练，不仅可以考查到学生的理解和掌握情况，也可以督促学生有针对性的进行归纳和总结。因此，我将布置一些关于相似三角形的经典中考题：

1.如图所示，△ABC∽△ADE，且，下列正确的是（ ）

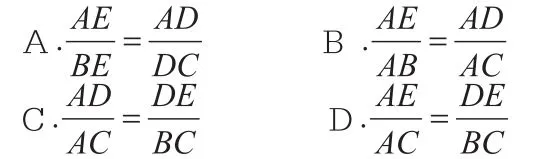
2.如图所示，在平行四边形ABCD中，，。（1）求证△ABE∽△ADF；（2）若AG=AH，求证四边形ABCD为菱形。

3.如图所示，1m长的标杆的影长1.2m，求AB的高度。

通过运用习题训练的方式，使学生对知识点的掌握更加扎实，从而实现对其的灵活运用。

为了能让学生在见识到各式各样的题目后意识到知识点掌握的重要性，从而重视学习知识点，养成努力学习的习惯，需要注意的是，我们在布置题目的时候既要始终贴近重难点，也要保证题目类型的多样化。

综上所述，在复习相似三角形时，要从学生的角度出发，让学生从发现问题到解决问题，最后到精益求精，循序渐进，切不可为了求速度而忽视了学生的实际情况。因此，作为教育工作者，要更加注重对教学方案的设计和教学方式的创新，既要传授知识给学生，也要注重培养其思维的发展和能力的提升，这样不仅可以推进新课改的顺利实施，也可以极大程度地提高课堂教学效率。