“函数的单调性”的教学设计

江苏省南京市六合区程桥高级中学 蔡红艳

“函数的单调性”的教学设计

江苏省南京市六合区程桥高级中学 蔡红艳

教学目的：

1.理解函数单调性概念，掌握判断函数单调性的方法，会证明一些简单函数在某个区间上的单调性，体验用数学语言刻画函数单调性的必要性。

2.经历函数单调性的探究过程，体验数学语言的准确简洁之美。

教学重点：函数单调性的概念与判断及证明。

教学难点：函数单调性概念的形成；运用定义证明函数的单调性。

教学过程：

一、问题情境

问题：观察图像，说出气温在哪些时间段内是升高的？怎样用数学语言刻画“一定时段内，随着时间的推移气温逐步升高”这一特征？

二、学生活动

问题1：画出下列函数的图像，请你说说这些函数的图像有什么变化趋势。

学生通过作图可以观察得到：随着x值的增大，函数图象有的呈逐渐上升的趋势，有的呈逐渐下降的趋势，有的在一个区间内呈上升的趋势，在另一区间内呈逐渐下降的趋势.

师：你能明确说出“图像呈逐渐上升趋势”的意思吗？

生讨论得到：在某一区间内，当x的值增大时，函数值y也逐渐增大⇔图象在该区间内呈上升趋势；当x的值增大时，函数值y反而减小⇔图象在该区间内呈下降趋势。

师总结：上升、下降趋势，其实说的就是函数的单调递增和单调递减。

师：感知图像y=1，它在定义域R上是上升的吗？

生：不是，平行于x轴。

师：那我将函数y=1的图像变成函数y=0.000001x+1的图像，如图所示，它现在还是平行于x轴吗？

生：感觉还是的。

师：实际上，这条直线k=0.000001，必过一、三象限，应该是一条呈上升趋势的直线，眼睛有时会欺骗我们，因此还得学会其他的办法去判断。

三、建构数学

问题3：如何用数学语言来准确地表述函数的单调性呢？

例如：关注函数y=x3的图像在R上随着x的变化，y又是如何变化的呢？

生：画图研究。

师：如何画？

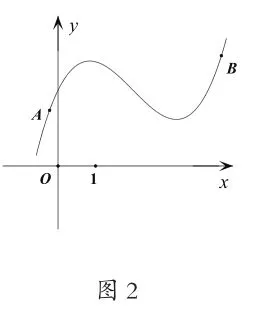
生：1列表；2.平面上绘制点；3.用一条平滑的曲线连接如图所示。

师：从A到B呈上升趋势，那么A、B两点之间如何连接？

生1：在A、B两点之间取更多的点来做试验，然后连接。

生2：补充，就算取再多的点，每两点之间依然还是有A、B之间的问题。

生3：如果能取到足够多的点，使得A、B之间几乎无空隙，那就不存在问题了。

生4：要是能取到所有的点就好了。

师评点：取到所有的点，实际操作不太可能，足够多的点又有可能发生右图的情况。

问题：如何用数学语言精确刻画函数y=f（x）在区间I上y随着x的增大而增大？

我们要有严格的定义，板书：

一般地，设函数的定义域为A，区间,如果对于区间I内的任意两个值x1，x2，当x1＜x2时，都有f（x1）＜f（x2），那么就说函数f（x）在区间I上是单调增函数，I称为y=f（x）的单调增区间。

如果对于区间内的任意两个值x1，x2，当x1＜x2时，都有f（x1）＞f（x2），那么就说y=f（x）在区间I上是单调减函数，I称为y=f（x）的单调减区间。

四、数学应用

例1：判断题。

②定义在R上的函数f（x）满足f（2）＞f（1），则称函数f（x）是R上的增函数；

③函数f（x）是R上的增函数，则必有f（2）＞f（1）；

④定义在R上的函数f（x）满足f（2）＞f（1），则函数f（x）在R上不是减函数；

⑤若定义在R上的函数f（x）在区间(-∞，0]上是单调增函数，在区间[0，+∞)上也是单调增函数，则函数f（x）在R上是单调增函数；

⑥若定义在R上的函数f（x）在区间(-∞，0]上是单调增函数，在区间（0，+∞)上也是单调增函数，则函数f（x）在R上是单调增函数；

解：（1）错；（2）错；（3）对；（4）对；（5）对；（6）错。

例2：作出下列函数的图象，并写出函数的单调区间。

解：（1）函数y=-x2+2的图像如图3所示，单调增区间为(-∞，0]，单调减区间为[0，+∞]。

板书：【小结】证明函数在某个区间上的单调性的步骤：

（1）取值：在给定区间上任取两个值x1，x2且x1＜x2；

（3）定号：判断上式的符号，若不能确定，则分区间讨论；

（4）结论：根据差的符号，得出单调性的结论。

五、回顾小结

本节课主要学习了函数单调性的概念以及判断函数在某个区间上的单调性的方法。

六、课外作业

1.习题2.2.第1题、第2题、第4题、第10题。