分析高中数学三角函数解题常见误区及正确解题方案

江苏省白蒲高级中学 宗位勇

分析高中数学三角函数解题常见误区及正确解题方案

江苏省白蒲高级中学 宗位勇

三角函数是以角度或弧度为自变量，将自变量对应的终边与单位圆交点坐标或者比值为因变量的函数。在高中数学三角形、圆形等几何形状性质的研究中具有重要的作用，同时也是周期性数学现象研究的基础工具。在高中数学考试中，三角函数占有较大的比例，以概念、定义域、三角形内角、值域、向量的变化为基本内容。本文以苏教版高中数学教材为例，重点分析三角函数解题常见的误区，并附正确解题方案，为高中数学三角函数教学提供参考。

高中数学；三角函数；解题误区；正确解题方案

三角函数是高中数学教学中的重点内容，同时也是学生普遍反映难以理解和掌握的知识点。三角函数的灵活运用是学好高中数学的基础，也是研究几何图形性质的重要工具[1]。笔者总结多年的教学经验，发现学生在三角函数解题中主要出错的地方在于对向量公式、原理把握不佳，抽象思维能力较差等，导致求三角函数值、图像平移、单调性等方面较易出错且应用不够灵活。现将高中数学三角函数解题常见误区和正确解题方案进行分析，报告如下。

一、解题过程中粗心大意，忽略三角函数名称

如：已知sinα＞sinβ，且两角在同一象限，则下列命题成立的是：（ ）

A.若两角在第一象限，则cosα＞cosβ

B.若两角在第二象限，则tanα＞tanβ

C.若两角在第三象限，则cosα＞cosβ

D.若两角在第四象限，则tanα＞tanβ

注：若α与β均在第一或第三象限，那么由sinα＞sinβ可知，cosα＜cosβ，因此可将A选项和C选项排除；若α与β均在第二象限，那么由sinα＞sinβ可知tanα＜tanβ，可排除B选项。若两角均在第四象限可知tanα＞tanβ，故而D选项正确。要想正确解答本题，必须熟悉掌握不同象限角正弦函数与余弦函数、正切函数的增减性是否相同。

分析：本题出错的根本原因在于学生对于不同象限不同形式的三角函数增减性掌握效果不理想，第一象限、第三象限中正弦函数与余弦函数增减性刚好相反；第二象限中正弦函数和正切函数增减性也相反；第四象限中正弦函数与正切函数增减性相同。此外，教师可以教会学生在难以熟记不同象限不同三角函数形式增减性的情况下，可以首先学会画函数y=sinx，y=cosx，y=tanx的图像，并以图像分析增减性，避免死记硬背造成知识掌握情况混乱。

二、求解过程中忽略三角函数图像变形

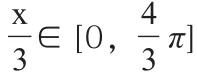
分析：学生本题出错的重点在于对三角函数图像及变化情况、性质掌握情况不佳，教师应当针对此种情况和问题细致分析原因，通过提问学生了解其思维方式和想法，反复向学生讲解正确的解题思路和方法，以加深其对三角函数相关知识的掌握情况和理解程度。

三、三角函数平移概念把握不佳

如：将曲线ycosx+2y=1首先沿着x轴方向向右平移，平移幅度为个单位，然后沿着y轴向下平移，平移幅度为1个单位，可以得到方程（ ）。

A.（1-y）sinx+2y=3 B.（y-1）sinx+2y=3；

C.（y+1）sinx+2y=-1 D.-（y+1）sinx+2y=-1

四、不能熟练应用三角函数特性

如：若sinα+cosα=1，则对于任意实数n，sinnα+cosnα应为（ ）。

注：部分学生在解题过程中不能熟练应用三角函数特性，甚至认为既然题目中提到实数n，结果肯定就会和n有关系，甚至干脆胡乱选一个，但实际上并不理解本题的正确解答方法。以下提供2种解题方法：

方法1：充分利用sin2α+cos2α=1公式，将sinα设为x，将cosα设为y，可知x2+y2=1，联合x+y=1，求解可知x=0，y=1或x=1，y=0，也就是说sinα=0，cosα=1，或sinα=1，cosα=0，即sinnα+cosnα=0n+1n=1，由此可知，本题的正确答案应当选A。

方法2：采用赋值法，令sinα=0，cosα=1，或sinα=1，cosα=0，可得sinnα+cosnα=0n+1n=1，即得正确答案。

分析本题出错的原因主要是学生看到出现实数n一下难以理解，再加上可能基础知识掌握不牢靠，导致对任意选择带有n的选项或者不确定，即C或D，胡乱填写。其实本题出错的根本原因在于忽略了sin2α+cos2α=1公式[3]。因此在高中数学三角函数学习中要求学生必须熟练掌握三角函数特性及相关性质、定理和公式，方能将其充分、灵活应用于解题过程中，提高答题正确率。

总之，高中数学三角函数是教学的重点和难点，为更好地完成教学任务，数学教师应在面临诸多问题的情况下通过不断的探索和总结发现学生的解题误区；对考试热点和难点着重讲解。此外，还需要让学生意识到只有正确熟练掌握三角函数相关的概念、公式、平移特性、角的变化范围及值域变化情况，多做练习并学会自己总结经验，才有可能避免三角函数解题过程中经常出现的错误，取得良好的学习成绩，同时也能促使教师更高质量的完成教学任务。

[1]宋艳丽.略谈高中数学三角函数教学策略[J].才智，2012（25）：122-123.

[2]吴义平.高中数学三角函数教学要点分析[J].学周刊，2016（28）：104-105.

[3]郭新艳.高中数学三角函数教学要点初析[J].品牌，2015（03）：223.