基于磷虾群算法的汽轮机热耗率建模应用

牛培峰， 陈 科， 马云鹏， 赵庆冲， 李国强

(燕山大学 工业计算机控制工程河北省重点实验室，河北秦皇岛 066004)



基于磷虾群算法的汽轮机热耗率建模应用

牛培峰， 陈 科， 马云鹏， 赵庆冲， 李国强

(燕山大学 工业计算机控制工程河北省重点实验室，河北秦皇岛 066004)

为了准确建立汽轮机热耗率预测模型，以某热电厂600 MW超临界汽轮机组为研究对象，采用基于反向学习自适应的磷虾群算法(OAKH)和快速学习网(FLN)进行综合建模，并将该模型的预测结果与基本快速学习网、粒子群算法、生物地理学优化算法和磷虾群算法优化的快速学习网模型的预测结果进行比较.结果表明：OAKH算法能够更好地优化FLN模型参数，使所建立的FLN汽轮机热耗率预测模型具有更高的预测精度和更强的泛化能力，能够准确、有效地预测热电厂的汽轮机热耗率.

汽轮机； 热耗率； 磷虾群算法； 快速学习网； 反向学习算法

汽轮机热耗率是影响热电厂热效率的重要因素之一，实时且精确的热耗率预测是评价汽轮机热经济性能的关键.目前，我国大多数发电机组的负荷率不高，据统计多在65%～75%负荷下运行，这就使得机组的热经济性降低[1].

现场采用质量和能量平衡方程来计算热耗率值，但由于受到机组运行过程中热力参数波动等影响，导致模型所得热耗率值会产生偏差.目前，许多学者采取回归模型的方法来计算汽轮机热耗率值.王惠杰等[2]提出基于v类型支持向量机(v-SVM)的汽轮机热耗率回归预测模型；牛培峰等[3]提出汽轮机热耗率多模型建模方法；朱誉等[4]提出基于BP神经网络的汽轮机热耗率在线计算方法.然而，影响汽轮机组热耗率的因素有很多，且汽轮机组的工作过程具有非线性、时变和多工况的特点，很难用机理模型来描述.为克服该缺点，借助神经网络较强的非线性拟合能力、网络泛化及容错能力，笔者提出了改进的磷虾群算法(即基于反向学习自适应的磷虾群算法，OAKH算法)和快速学习网(FLN)[5]的综合建模方法.

磷虾群(KH)算法是2012年由美国阿克伦大学的Gandomi等[6]提出的一种新的启发式优化算法，由于其搜索多样性强、操作简单和调整参数少而得到广泛应用.然而在处理复杂的优化问题时，KH算法易陷入局部最优且收敛精度低；FLN通过求解线性方程组，将最小二乘范数解作为网络权值，但是FLN模型对初始的权值和阈值过于依赖.为了克服上述缺陷，笔者提出了OAKH算法，利用某热电厂600 MW超临界汽轮机组运行数据建立了FLN汽轮机热耗率预测模型(以下简称FLN模型)，并应用OAKH算法解决了FLN模型的参数优化问题.最后，为了验证模型的准确性和有效性，将该模型与其他几种FLN模型进行了对比研究.

1 磷虾群算法和快速学习网

1.1 磷虾群算法

KH算法是对磷虾觅取食物和增加种群密度行为进行的模拟[7].在KH算法中，每只磷虾位置代表一个可行解.在海洋生活中，磷虾个体的位置会受到以下3个因素影响[8].

(1)种群位置迁移引起的个体游动.

Ni,new=Nmaxαi+ωnNi,old

(1)

式中：αi为移动方向向量，αi=αi,local+αi,target，其中αi,local和αi,target分别为局部邻近个体的感应方向向量和种群最优个体提供的方向向量；Nmax为最大感应速度，取0.01 m/s；ωn为惯性权值，取值范围为[0,1]；Ni,old为上次的位置变化；Ni,new为当前的位置变化.

(2)觅食行为.

Fi=Vfβi+ωfFi,old

(2)

式中：βi为磷虾个体觅食方向向量，βi=βi,food+βi,best，其中βi,food和βi,best分别为食物源和当前最优磷虾位置的方向向量；Vf为觅食的速度，取0.02 m/s；ωf为惯性权值，取值范围为[0,1]；Fi,old为第i个磷虾个体上次觅食运动所产生的位置变化；Fi为当前第i个磷虾个体的位置变化.

(3)磷虾个体的随机扩散.

Di=Dmaxδ

(3)

式中：Dmax为磷虾个体的最大扩散速度；δ为一个随机的扩散方向向量，取值范围为[-1,1]；Di为随机扩散引起的位置变化.

针对不同的磷虾个体，其位置越好，扩散越不明显.以上3个因素将会使磷虾个体朝着适应度值最小的方向改变自身的位置，使可行解朝着最优解方向进化.其中种群位置迁移引起的个体游动和觅食行为都包含了一个全局搜索策略和一个局部搜索策略，这2种策略并行进行，使得该算法成为一种稳定有效的优化算法[9].

综上所述，从t时刻到t+Δt时刻的位置矢量为：

(4)

式中：Δt为时间间隔;ΔT为速度矢量步长调节因子.

1.2 快速学习网

FLN是基于极端学习机思想提出的一种新型双并联前馈神经网络，与极端学习机最大的区别就是在单隐藏层神经网络的基础上增加了输入层与输出层的直接联系[10].因此，FLN可以看成是一种隐藏层到输出层的非线性与输入层到输出层的线性组合模型，其应用前景广泛.FLN的结构如图1所示.

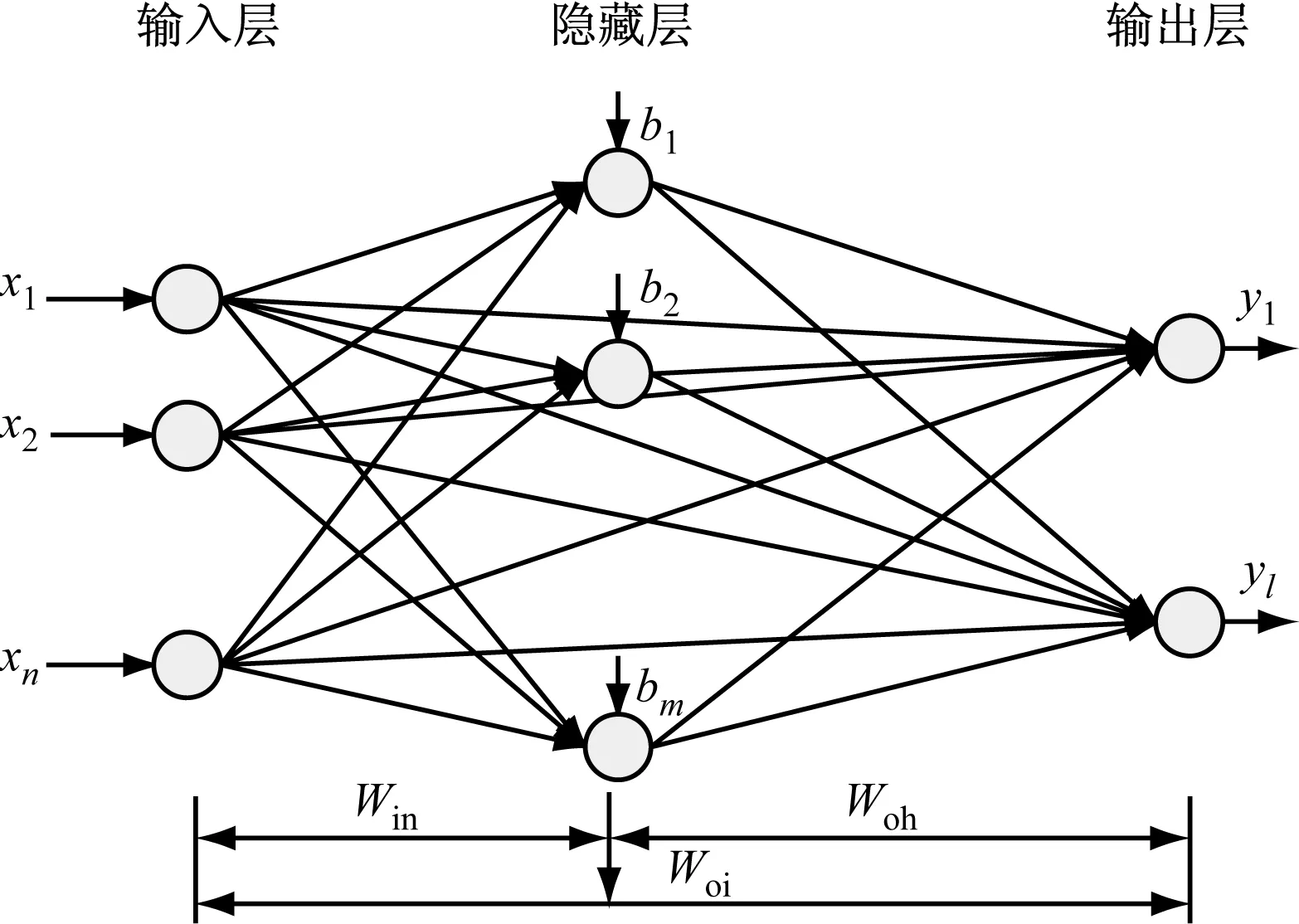
图1 快速学习网结构图

对于任意N个随机样本{(xi,yi)},i=1,2,…,N，其中，xi=[xi1,xi2,…,xin]T∈Rn表示第i个样本的n维特征向量，yi=[yi1,yi2,…,yil]∈Rl表示第i个样本的l维输出向量.令隐藏层神经元数为m个，隐藏层激活函数为g(x)，则数学模型如下：

(5)

式中：i=1,2,…,N；Woi为输入层与输出层之间的连接权值；Wk,in为输入层到第k个隐藏层神经元之间的连接权值；Wk,oh为第k个隐藏层神经元到输出层之间的连接权值；bk为第k个隐藏层神经元的阈值.

式(5)用矩阵形式可表达为：

(6)

(7)

(8)

式中：W为输出权值矩阵；G为隐藏层输出矩阵；Y为期望输出.

式(6)用最小二乘范数求解可得：

(9)

(10)

FLN算法步骤如下：(1)随机生成输入权值矩阵Win和隐藏层阈值矩阵b；(2)通过式(8)计算隐藏层输出矩阵G；(3)通过式(9)计算输出权值矩阵W；(4)通过式(10)将输出权值矩阵W分割为Woi和Woh.

2 改进的磷虾群(OAKH)算法

与其他优化算法相比，KH算法的优势在于其搜索多样性强、操作简单和调节参数少，且其搜索为随机方式，与传统的梯度搜索有很大不同[11].但是，KH算法中的搜索完全依赖随机性，导致该算法收敛精度低，且不易跳出局部最优[12-13].

针对上述KH算法的缺陷，笔者提出了OAKH算法.改进后的算法具有较强的全局搜索能力，同时收敛速度和收敛精度也得到了较大幅度的提高，主要有以下2个改进点.

(1)采用反向学习算法[14]进行种群位置初始化，可以有效提高初始化种群位置的质量.

在OAKH算法中，基于反向学习算法的种群位置初始化过程表述如下(其中NP为可行解的维数，NK为种群数量，C为当前迭代次数)：

①初始化种群位置P(C=0)={xij}，i=1,2,…,NP，j=1,2,…,NK.

(11)

式中：xi,min和xi,max分别为第i维元素的最小值和最大值.

③从组合种群位置{P(C=0)∪P′(C=0)}中选择NK个适应度值较小的位置作为初始种群位置.

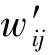
Xi(t+Δt)=Xi(t)wij+

(12)

wij=φ=1/[1+exp(-fj/a)u]

(13)

(14)

式中：a为在第一次迭代中种群位置最优的适应度值；u为当前迭代次数；fj为第j个磷虾的适应度值.

OAKH算法流程如下：(1)初始化参数设定，即种群数量NK、最大迭代次数MI、最大感应速度Nmax、觅食速度Vf和磷虾个体的最大扩散速度Dmax等；(2)在可行域空间内利用反向学习算法初始化磷虾种群的位置；(3)计算每一只磷虾相应的适应度值，并选择NK个适应度值较小的位置作为初始种群位置；(4)根据选定的NK个适应度值较小的位置，计算磷虾个体相应的适应度值；(5)计算由磷虾群位置迁移引起的个体游动、觅食行为和由于随机扩散而产生的磷虾个体位置的变化量；(6)利用改进后的位置矢量更新公式(12)产生下一代的位置；(7)计算新产生位置矢量的适应度值，重复步骤(5)～步骤(7)，直到达到最大迭代次数，该算法结束；(8)输出最优个体，即该算法找到的最优解.

3 OAKH算法性能测试

为了验证OAKH算法的有效性和可行性，采用6个典型的基准测试函数进行仿真分析，并与基本的KH算法、粒子群(PSO)算法和生物地理学优化(BBO)算法进行比较.6个基准测试函数见表1，其中前3个为单峰基准函数，后3个为多峰基准函数.PSO参数设置为学习因子c1=c2=1.5；BBO参数设置为突变概率Mu=0.005，混合迁移算子μ=0.8；OAKH算法参数设置与KH算法相同，最大感应速度Nmax=0.01 m/s，觅食速度Vf=0.02 m/s，磷虾个体最大扩散速度Dmax=0.005 m/s.

表1 6个基准测试函数

为了进行公平性比较，OAKH算法、KH算法、PSO算法和BBO算法4种算法的其他相关参数设置相同，初始化种群数量为40，最大迭代次数为500，运行次数为20，维数设置为10、30和50 3种.对20次寻优的平均值和均方差进行记录，结果见表2.

从表2可以看出，在设定的参数条件下，OAKH算法能够找到f1、f3、f4、f5和f6的理论最优值，或者非常接近，可以近似看成理论最优值，并且随着维数的上升，OAKH算法较其他3种算法更加稳定，搜索的精度也更高.对于f2，虽然OAKH算法精度没有达到理论最优值，但与其他3种算法相比，其搜索的结果也相对准确，特别是在高维搜索中.尽管OAKH算法对f2、f3、f6在10维的搜索精度不如PSO算法，但相比于基本的KH算法其精度提升较大.对于绝大部分的基准测试函数来说，与其他3种算法相比，OAKH算法不仅跳出局部最优的能力更强、搜索的精度更高，而且更适合在高维参数优化中应用.

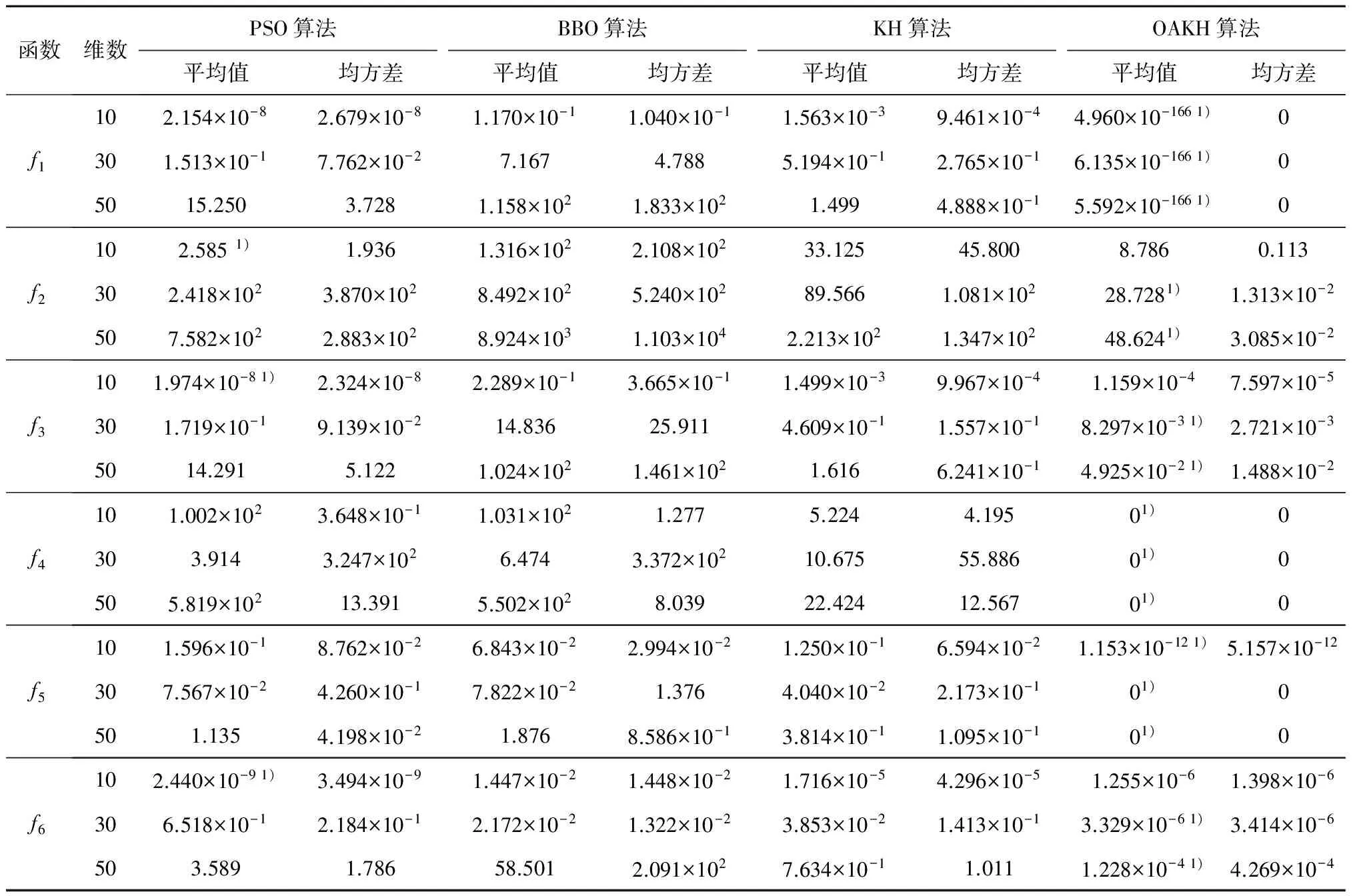
表2 4种算法对基准测试函数的运行结果

注：1)该数字表示最好的结果.

4 汽轮机热耗率建模

汽轮机热耗率是指汽轮发电机组每发1 kW·h电量所消耗的热量，是反映机组能量转换过程中一项重要的经济指标[15].对机组进行热耗率建模，比较热耗率与热力参数之间的关联强度，选择关联度较大的一些参数.根据这个原则并结合相关资料[16]，选择发电负荷、主蒸汽压力、主蒸汽温度、再热器出口蒸汽压力、再热器出口蒸汽温度、再热器入口蒸汽压力、再热器入口蒸汽温度、再热减温水流量、过热减温水流量、汽轮机背压、循环水进水口温度和给水流量共12个参数作为汽轮机热耗率预测模型的输入，热耗率作为输出.热耗率值的计算详见文献[17].

4.1 模型建立及参数优化

以某热电厂600 MW超临界汽轮机组为研究对象，从集散控制系统(DCS)数据库中随机采集10 d正常供热运行数据，其中春、夏、秋、冬4季各采集的天数为2 d、2 d、3 d、3 d，每隔2 h采集一次，每天12组，每组均包含上述12个自变量参数，总共采集了120组多工况运行数据，机组负荷的范围在298.455～563.555 MW内，基本覆盖了机组全天运行的典型工况.应用FLN建立模型，随机选择8 d的96组运行数据作为训练样本，剩下的24组运行数据作为预测样本，预测样本用于验证所建模型的预测精度和泛化能力.

对于随机初始输入权值和隐藏层阈值的FLN，很难确保得到的FLN模型具有较高的预测精度和较好的泛化能力.针对上述不足，利用OAKH算法对FLN模型的输入权值和隐藏层阈值进行优化，以目标函数适应度值最小为原则，通过判断是否达到最大迭代次数为循环终止条件.当循环结束后，将最优模型结构参数作为输入权值和隐藏层阈值代入FLN模型，即可完成OKAH-FLN模型的建立.具体的模型优化过程详见图2.

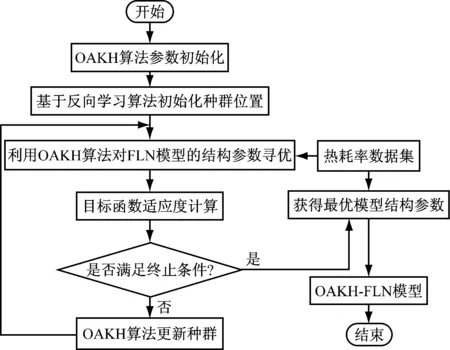
图2 采用OAKH算法优化FLN结构参数的流程图

OAKH算法的参数设置与前面相同.FLN参数设置如下：3层网络结构为12-20-1，隐藏层激活函数为sigmoid，输入权值和隐藏层阈值的寻优范围均为[-1,1]，通过多次仿真实验，确定循环迭代次数为200.

在模型结构参数优化中，目标函数为：

,

i=1,2,…,N

(15)

式中：Yi为模型的训练输出热耗率，kJ/(kW·h)；Yi′为实际热耗率，kJ/(kW·h).

4.2 模型性能分析

在OAKH-FLN模型中，由96组训练样本建立汽轮机热耗率预测模型，并用24组测试样本对模型的预测精度和泛化能力进行验证.仿真结果如图3和图4所示，其中实际值是通过计算所得对应组号的汽轮机热耗率值.

图3 训练样本预测值与实际值的对比

Fig.3 Comparison of training data between predicted results and actual measurements

图4 测试样本预测值与实际值的对比

Fig.4 Comparison of testing data between predicted results and actual measurements

为了更好地体现OAKH-FLN模型的预测效果，同时采用FLN模型、KH-FLN模型、PSO-FLN模型和BBO-FLN模型对汽轮机热耗率进行了预测.为了综合评价5种模型预测值的准确度，这里引入3个性能评价指标：均方根误差(RMSE)、平均绝对百分比误差(MAPE)和平均绝对误差(MAE).5种模型的变量类型、参数设置和数据样本与OAKH-FLN模型相同，各算法参数的设置与上文一致，预测结果如表3和表4所示.

由图3可知，OAKH-FLN模型对训练样本的拟合度和预测精度均较高.如表3所示，对于训练样本，OAKH-FLN模型的RMSE为5.497，MAPE为4.886×10-9，MAE为4.272，3个性能评价指标均小于其他4种模型；与FLN模型相比，OAKH-FLN模型的RMSE降低了18.961，MAPE降低了9.066×10-8，MAE降低了14.271.因此，对于训练样本而言，OAKH-FLN模型比其他4种模型具有较强的辨识能力和较高的拟合精度.

表3 训练样本准确度对比

表4 测试样本准确度对比

由图4可知，OAKH-FLN模型能够对测试样本进行较好的预测，且相比于FLN模型其预测精度提升很大.如表4所示，对于测试样本，OAKH-FLN模型的RMSE为12.158，MAPE为2.071×10-5，MAE为10.098，3个性能评价指标均小于其他4种模型；与FLN模型相比，OAKH-FLN模型的RMSE降低了19.178，MAPE降低了1.101×10-5，MAE降低了14.462.因此，对于测试样本而言，OAKH-FLN模型比其他4种模型具有较强的泛化能力和较高的预测精度.

结合图3、图4、表3和表4，对比拟合情况和各个性能评价指标可知，OAKH-FLN模型比其他4种模型具有较强的辨识能力和预测能力，能够精确地对汽轮机热耗率进行预测.

5种模型对测试样本的预测误差曲线如图5所示.从图5可以看出，OAKH-FLN模型的预测误差比较平稳，主要在0点附近波动，最大预测误差为25.707 kJ/(kW·h)；与其他4种模型的预测误差相比，OAKH-FLN模型的预测误差明显更小，这说明OAKH-FLN模型能够更加准确地预测汽轮机的热耗率.

图5 各模型对测试样本的预测误差曲线

综上所述，对于本文研究对象，OAKH算法能够更好地优化汽轮机的结构参数，所建立的OAKH-FLN模型具有较强的泛化能力和较高的预测精度，非常适合用于工程中预测汽轮机热耗率.

5 结 论

以某热电厂600 MW超临界汽轮机组为研究对象，以现场采集的运行数据为样本，利用基于反向学习自适应的磷虾群算法优化快速学习网的模型参数，建立了OAKH-FLN模型来准确预测汽轮机热耗率，并将该模型的预测结果与FLN模型、KH-FLN模型、PSO-FLN模型和BBO-FLN模型的预测结果进行对比.结果表明：OAKH-FLN模型能够更加准确、有效地预测汽轮机热耗率，为热电厂预测汽轮机热耗率提供了一种新方法.

[1] 张春发, 王惠杰, 宋之平, 等. 火电厂单元机组最优运行初压的定量研究[J]. 中国电机工程学报, 2006, 26(4): 36-40.

ZHANG Chunfa, WANG Huijie, SONG Zhiping,etal. Quantitative research of optimal initial operation pressure for the coal-fired power unit plant[J]. Proceedings of the CSEE, 2006, 26(4): 36-40.

[2] 王惠杰, 陈林霄, 李洋, 等. 基于v-SVM的汽轮机热耗率回归模型研究[J]. 动力工程学报, 2014, 34(8): 606-611, 645.

WANG Huijie, CHEN Linxiao, LI Yang,etal. Study on heat rate regression model of steam turbines based on v-SVM[J]. Journal of Chinese Society of Power Engineering, 2014, 34(8): 606-611, 645.

[3] 牛培峰, 刘超, 李国强, 等. 汽轮机热耗率多模型建模方法研究[J]. 计量学报, 2015, 36(3): 251-255.

NIU Peifeng, LIU Chao, LI Guoqiang,etal. Investigation on multi-model modeling method of steam turbine heat rate[J]. Acta Metrologica Sinica, 2015, 36(3): 251-255.

[4] 朱誉, 冯利法, 徐治皋. 基于BP神经网络的热经济性在线计算模型[J]. 热力发电, 2008, 37(12): 17-19, 30.

ZHU Yu, FENG Lifa, XU Zhigao. An on-line calculation model of thermal economic efficiency based BP neural network[J]. Thermal Power Generation, 2008, 37(12): 17-19, 30.

[5] LI Guoqiang, NIU Peifeng, DUAN Xiaolong,etal. Fast learning network: a novel artificial neural network with a fast learning speed[J]. Neural Computing and Applications, 2014, 24(7/8): 1683-1695.

[6] GANDOMI A H, ALAVI A H. Krill herd: a new bio-inspired optimization algorithm[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(12): 4831-4845.

[7] WANG Gaige, GUO Lihong, WANG Heqi,etal. Incorporating mutation scheme into krill herd algorithm for global numerical optimization[J]. Neural Computing and Applications, 2014, 24(3/4): 853-871.

[8] WANG Gaige, GUO Lihong, GANDOMI A H,etal. Chaotic krill herd algorithm[J]. Information Sciences, 2014, 274: 17-34.

[9] 牛培峰, 杨潇, 马云鹏, 等. 基于改进的磷虾群优化算法的汽轮机初压优化研究[J]. 动力工程学报, 2015, 35(9): 709-714.

NIU Peifeng, YANG Xiao, MA Yunpeng,etal. Optimization on initial pressure of a steam turbine based on improved krill herd algorithm[J]. Journal of Chinese Society of Power Engineering, 2015, 35(9): 709-714.

[10] 李国强. 新型人工智能技术研究及其在锅炉燃烧优化中的应用[D]. 秦皇岛: 燕山大学, 2013.

[11] LI Junpeng, TANG Yinggan, HUA Changchun,etal. An improved krill herd algorithm: krill herd with linear decreasing step[J]. Applied Mathematics and Computation, 2014, 234: 356-367.

[12] WANG G G, GANDOMI A H, ALAVI A H. Stud krill herd algorithm[J]. Neurocomputing, 2014, 128: 363-370.

[13] WANG G G, GANDOMI A H, ALAVI A H. An effective krill herd algorithm with migration operator in biogeography-based optimization[J]. Applied Mathematical Modelling, 2014, 38(9/10): 2454-2462.

[14] RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Opposition-based differential evolution (ODE) with variable jumping rate[C]//IEEE Symposium on Foundations of Computational Intelligence. Honolulu, USA: IEEE, 2007: 81-88.

[15] 刘超, 牛培峰, 游霞. 反向建模方法在汽轮机热耗率建模中的应用[J]. 动力工程学报, 2014, 34(11): 867-872, 902.

LIU Chao, NIU Peifeng, YOU Xia. Application of reversed modeling method in prediction of steam turbine heat rate[J]. Journal of Chinese Society of Power Engineering, 2014, 34(11): 867-872, 902.

[16] 云曦, 阎维平. 火电厂汽轮机组影响热耗率计算的因素[J]. 东北电力技术, 2007, 28(3): 15-18.

YUN Xi, YAN Weiping. Factors effecting heat consumption calculation for steamed turbine of fossil-fired power plant[J]. Northeast Electric Power Technology, 2007, 28(3): 15-18.

[17] 盛德仁, 李蔚, 陈坚红, 等. 汽轮机组热耗率分析及实时计算[J]. 热力发电, 2003, 32(5): 16-18.

SHENG Deren, LI Wei, CHEN Jianhong,etal. Analysis and real-time calculation of specific heat consumption for steam turbine unit[J]. Thermal Power Generation, 2003, 32(5): 16-18.

Modelling of Turbine Heat Rate Based on Krill Herd Algorithm and Its Application

NIUPeifeng,CHENKe,MAYunpeng,ZHAOQingchong，LIGuoqiang

(Key Lab of Industrial Computer Control Engineering of Hebei Province, Yanshan University, Qinhuangdao 066004, Hebei Province, China)

To accurately predict the heat rate of steam turbine, a model was established with the sample data of a 600 MW supercritical steam turbine unit in a thermal power plant using opposition adaptive krill herd algorithm (OAKH) and fast learning network (FLN), of which the prediction results were compared with that of basic FLN model and those FLN models whose parameters were optimized by particle swarm optimization, biogeography-based optimization and krill herd algorithm. Results show that compared with other algorithms and models, the model of turbine heat rate based on OAKH algorithm has a higher accuracy in prediction and stronger capability in parameter optimization and generation, which may help to accurately and effectively predict the heat rate of steam turbines.

steam turbine; heat rate; krill herd algorithm; fast learning network; opposition-based learning algorithm

2016-01-05

2016-01-21

国家自然科学基金资助项目(61573306，61403331)

牛培峰(1958-)，男，吉林舒兰人，教授，博士生导师，研究方向为复杂工业系统的智能建模与智能控制和流程工业综合自动化等.电话(Tel.)：0335-8072979；E-mail：npf882000@163.com.

1674-7607(2016)10-0781-07

TK267

A 学科分类号：470.20