锥壳环向自动铺丝编程方法及铺放工艺性能①

文立伟，黄 威，王显峰，肖 军

(南京航空航天大学 材料科学与技术学院，南京 210016)

锥壳环向自动铺丝编程方法及铺放工艺性能①

文立伟，黄 威，王显峰，肖 军

(南京航空航天大学 材料科学与技术学院，南京 210016)

为解决复合材料锥壳环向自动铺丝编程问题，提出了按圆锥螺距进行锥壳自动铺丝编程的轨迹规划方法。根据圆锥螺旋角与螺距之间的关系式，通过改变螺旋角来保证螺距的恒定，继而实现自动铺丝过程中预浸纱无缝、无重叠、无增减纱。给出了在圆锥锥角较小情况下的一种简易铺丝编程方法。同时，通过计算该编程方法的铺放角与测地线轨迹的铺放角和固定角轨迹的铺放角之间的最大偏角，分析了该方法的铺放工艺性，并对该编程方法铺丝轨迹的最大测地曲率做了估算。最后，采用该方法对某机身尾锥试验件进行实际铺放验证。结果表明，提出的锥壳环向自动铺丝编程方法是合理的、正确的，具有良好的铺放工艺性。

复合材料；自动铺丝；轨迹规划；圆锥；工艺性能

0 引言

先进复合材料具有轻质、高强度、高模量、可设计性强、易于实现自动化整体化制造等特点，已广泛用于工业生产的各个领域，特别是航空航天等尖端技术领域[1-6]。自动铺丝技术可实现大尺寸、复杂形状复合材料构件的精密自动化成型制造，是复合材料低成本自动化成型技术的发展方向[7-11]。复合材料锥壳在航空航天领域应用广泛，如各类运载器与载荷的连接过渡段、火箭发动机喷管、人造卫星的炭纤维缠绕锥壳、飞机雷达罩等[12]。

在实际生产中，常采用固定角度铺层设计，以满足纤维按复合材料强度设计的方向排布；同时，为减小自动铺丝轨迹规划的难度，一般采用几组固定角度的铺层，如0°铺层、±45°铺层和90°铺层[13-14]。由于严格的90°铺层无法保证纤维的连续性，因此实际生产中，一般采用近90°铺层设计完成锥壳等回转体构件的环向铺放，但近90°固定角铺层轨迹设计存在增减纱的问题。传统成型方法对复合材料锥壳多采用纤维缠绕的方式进行成型加工，但缠绕成型无法进行0°铺层的成型，且缠绕成型中纤维张力在圆锥截面直径改变时，难以精确控制。鉴于此，本文对圆锥采用自动铺丝成型技术，由于铺放头压辊对模具的施压方式属于刚性施压，可随时根据圆锥截面直径的变化调整施压方向，保证铺放压力的精确控制。

针对铺放角连续变化的铺层设计方式，荷兰代尔夫特大学的研究人员提出了“变刚度”铺层铺放，他们研究了测地线方式、常曲率方式及角度线性变化方式的轨迹规划算法[15-17]。无论是目前采用传统的固定角度铺层，还是Blom等研究的“变刚度”铺层，都存在共同的缺点，即不可避免地存在间隙和重叠现象。

本文通过分析圆锥螺旋角与螺距的数学关系，提出根据圆锥螺距进行锥壳环向自动铺丝的编程方法，该方法通过适时调整铺放角(本文约定铺放角为圆锥螺旋角)，保持圆锥螺距恒定不变，避开了增减纱处理以及间隙和重叠的现象，提高了锥壳自动铺丝的工艺质量。

1 锥壳环向自动铺丝成型方法

1.1 原理与方法

假定锥面大端位于yoz平面内，大端截面圆圆心位于yoz平面的原点处，圆锥轴线位于x轴上且圆锥顶点位于x轴正方向上，如图1所示。其中，大端直径为2R，小端直径为2r，锥角为2α。

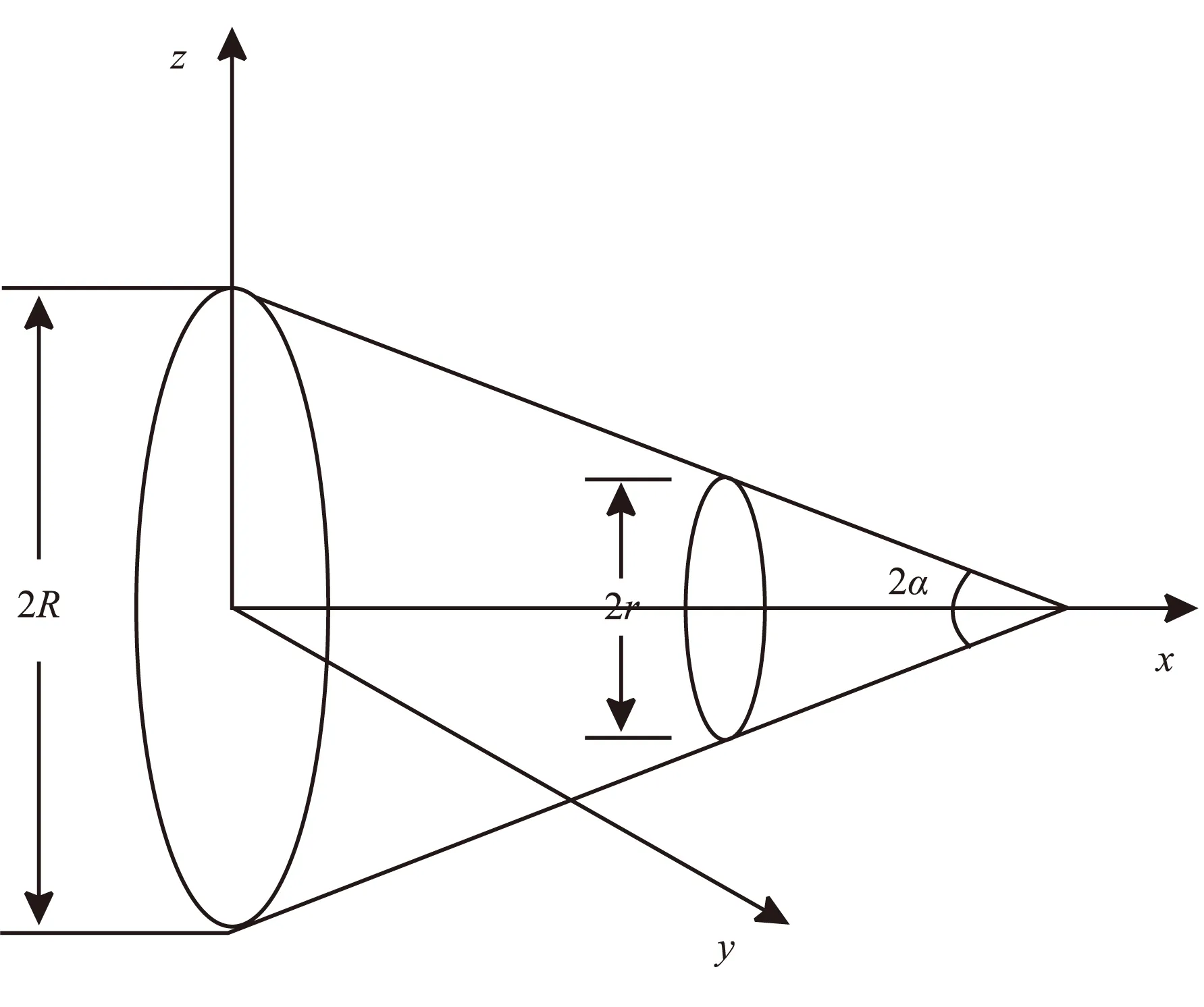
图1 锥壳示意图Fig.1 Diagram of conical shell

根据文献[18]，圆锥螺旋角和螺距之间的关系式为

(1)

式中S为螺旋线从起点上升一周沿母线方向的长度；d为锥壳上任一点处截面圆的直径；β为螺旋角。

对自动铺丝而言，当单丝宽度和丝束个数选定之后，在满足锥面满铺覆条件下，式(1)中S为常数。因此，圆锥螺旋角β仅随着锥壳截面圆直径d的变化而变化。

1.2 自动铺丝实现与编程

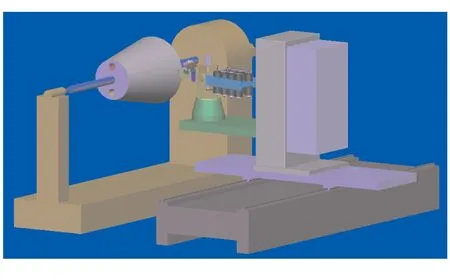
图2 铺丝机构模型图Fig.2 Diagram of model for automated fiber placed machine

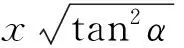
前面已有提到，在丝束满铺覆锥壳表面的条件下，压辊在锥壳表面运动的过程中，铺放角是随着锥壳截面圆直径的变化而变化的。因此，还必须适时调整压辊的前进方向，以保证预浸纱在铺覆锥壳表面的过程中始终沿着压辊的前进方向，从而保证铺放成型的质量。

根据上述分析，式(1)可写成:

于是，铺丝机构沿锥壳轴线方向每次步进长度x时，β的变化值可表示成如式(2)所示：

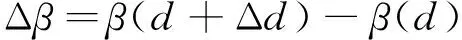
(2)

其中，Δd=-2xtanα。

至此，铺丝机构沿锥壳轴线方向每步进一次，对应的其他各轴的运动量便一一得到求解，根据待铺放锥壳的尺寸大小，借助计算机编程语言，将上述表达式循环一定的次数，即可得到锥壳环向自动铺丝的控制程序。综合上述分析过程，锥壳环向自动铺丝的编程流程如图3所示。

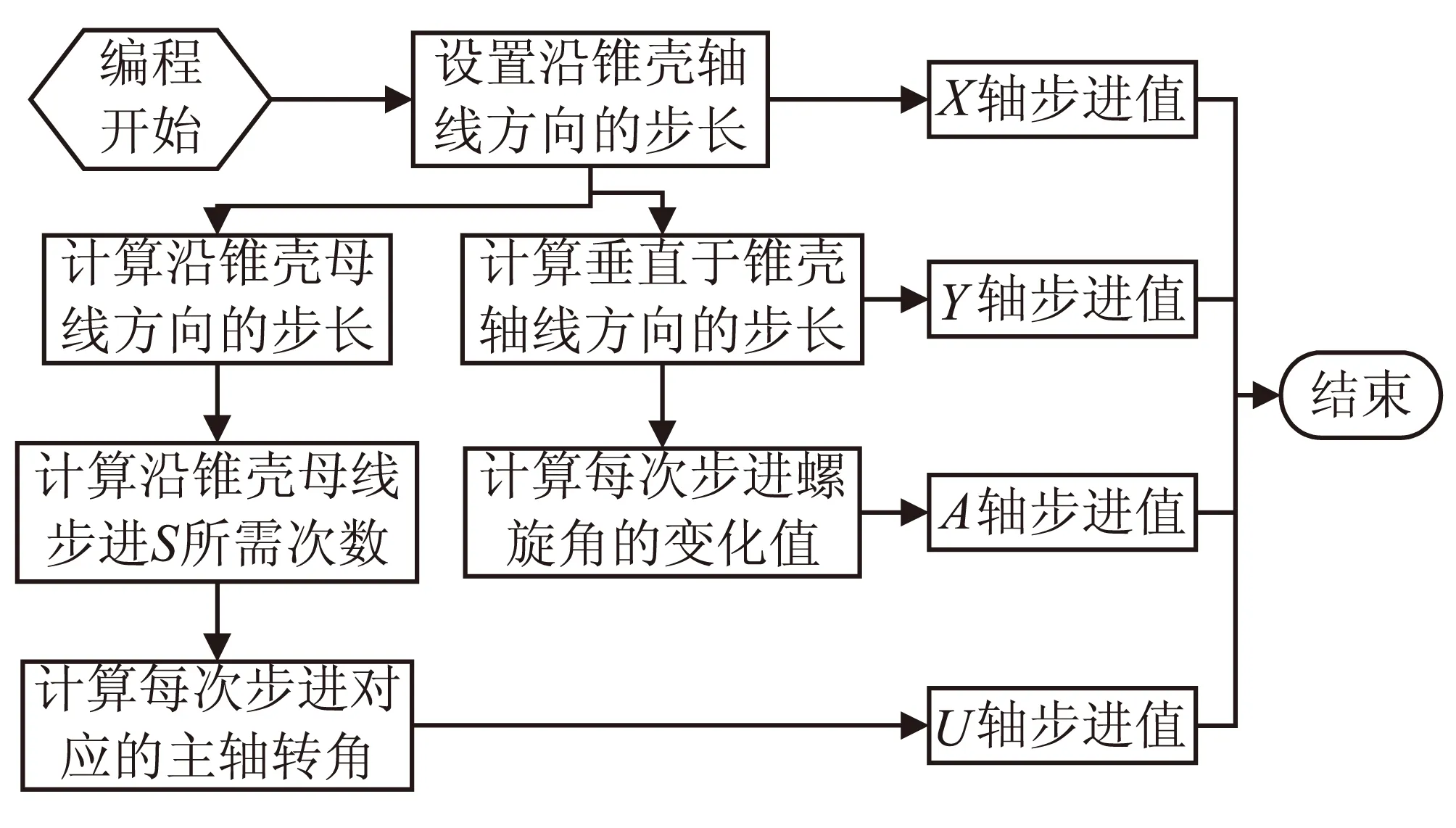
图3 锥壳环向自动铺丝编程流程Fig.3 Flow chart of automated fiber placement for large angle programming method of conical shell

对于锥壳自动铺丝从小端往大端铺覆成型的情况，只需根据机床坐标系调整起始铺放角和各轴运动插补值的符号即可实现，在此不再赘述。

2 铺放工艺性分析

铺放工艺性一般指轨迹的可铺性，即预浸纱在铺放过程中不发生屈皱变形的能力。预浸纱一般是由单向并排的增强纤维与树脂基体复合而成，由于预浸料中增强纤维弹性模量非常高，铺放过程中，纤维纵向拉伸变形能力有限，而纤维纵向受压缩作用产生的屈皱变形是预浸纱变形的主要机制[19]。

测地线是曲面上测地曲率为零的一条曲线，对可展曲面而言，测地线在展开面上是一条直线。因此，如果曲面上自动铺丝的轨迹按照测地线轨迹运动，将保证预浸纱在曲面上自由伸展而不发生褶皱，继而保证制品的铺放质量。当自动铺丝轨迹无法按测地线在曲面上运行时，铺丝轨迹曲线的测地曲率越小，也能保证较好的铺放工艺性[20]。基于此，将以前文所述编程方法的铺放角与测地线轨迹铺放角的偏差值作为分析编程方法的铺放工艺性的评判标准加以论述。

根据微分几何中刘维尔公式对测地线方程的推导[21]，存在如式 (3)所示的恒等式：

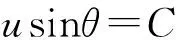
(3)

式中 u是回转体的周向截面半径；θ是曲面上测地线任一点处切线方向与回转体轴线的夹角；C为常数。

由式(3)不难看出，在锥壳铺丝轨迹按照测地线轨迹从锥壳大端往小端运动的过程中，铺放角是不断增大的。当铺放角θ增大到90°时，自动铺丝轨迹将无法往下继续进行。特别是，当锥壳大端起始铺放角接近90°时，测地线轨迹往前行进仅一小段距离便达到了铺放角等于90°的临界情况。对此，为保证自动铺丝的继续进行，需在铺放角达到90°的临界点之前，将铺放角按远离测地线轨迹的方向偏转，即将铺放角向起始铺放角偏转，从而保证铺放轨迹的连续性。值得注意的是，如果铺放角的偏转在起始铺放角和临界铺放角之间均匀变化，那么这条自动铺丝轨迹便转变成了固定角自动铺丝轨迹。根据1.2节对锥壳两端铺放角的计算可知，在铺丝轨迹从锥壳大端运动到小端的过程中，铺丝轨迹是按远离测地线方向偏转的。理论上，本文所述的编程方法似乎有悖于保证铺放工艺性，但经过计算，锥壳两端铺放角之差Δβmax=βR-βr，在锥角α取20.8°、R=442、r=298的情况下，Δβmax和Δγ=90-βr与S之间的对应关系如表1所示。其中，Δβmax表征了本文所述编程方法的铺放角对锥壳近90°固定角轨迹的最大偏角，Δγ表征了本文所述编程方法的铺放角对测地线轨迹的最大偏角，Δγ越大，相应的铺放工艺质量也就越差。

表1 Δβmax、Δγ与S的对应关系Table 1 Relationship between Δβmax、Δγ and S

由表1可知，Δβmax表征了本编程方法的铺放轨迹与固定角轨迹的近似程度。接下来，以圆锥固定角轨迹的测地曲率近似表征本文编程方法的测地曲率。

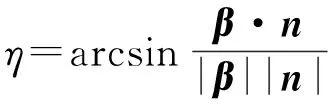
根据文献[22]，圆锥对数螺线上任一点的主曲率满足关系式：

(4)

式中d为螺线上任一点到圆锥轴线的距离。

将主曲率k沿测地曲率方向分解，可得圆锥对数螺线上任一点的测地曲率关系式为

(5)

由式(5)利用计算机编程语言，本文计算了锥角α=20.8°、R=442、r=298的锥壳在不同螺旋角下测地曲率随直径的变化关系，如图4所示。螺旋角越大的螺旋线，同一截面处的测地曲率越小，且测地曲率都随直径的增大而减小。由此可见，圆锥螺旋线的最大测地曲率在锥壳小端，以小端螺旋角89.5°为例，其最大测地曲率约为万分之六，在预浸纱有限的变形能力范围内，显然可满足良好的铺放工艺性。

综合表1和图4可知，圆锥螺旋角越大，螺旋线的最大测地曲率越小，本文所述编程方法的铺放工艺性越好，但螺旋角越大，铺放效率越低。对此，可根据铺放工艺质量和铺放效率，合理选取预浸纱的宽度和丝束个数，来达到二者的兼顾。

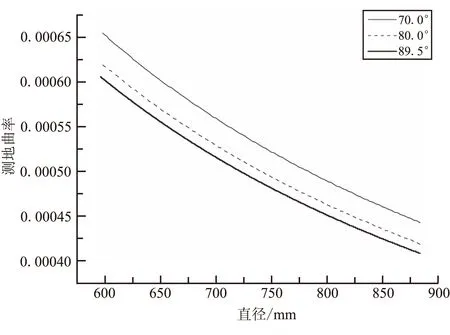
图4 不同螺旋角下测地曲率随直径的变化Fig.4 The relationship of geodesic curvature and diameter of the conic section with different the helix angle

最后，采用本文的编程方法，对某机身尾锥试验件进行了实际铺放验证，如图5所示，是采用2条6.35 mm预浸纱进行锥壳构件环向铺放的效果。可看出，预浸纱在模具表面铺覆良好，相邻预浸纱之间无缝无重叠，很好地验证了本文编程方法的正确性。

图5 锥壳环向铺放效果图Fig.5 Rendering of practical placement for conical shell when placement angle approach 90°

3 结论

(1)研究圆锥螺旋角与螺距的数学关系，提出了按照圆锥螺距进行自动铺丝编程的轨迹规划方法，通过调整螺旋角保证螺距恒定，实现了铺放过程中预浸纱的无缝、无重叠、无增减纱。

(2)提出了在锥壳锥角较小情况下的一种简易自动铺丝编程方法。

(3)分析了本文锥壳环向自动铺丝编程方法的铺放工艺性。

(4)以VC++ 6.0平台编写相关轨迹规划程序，以某机身尾锥试验件为例，进行实际铺放，验证了本文锥壳环向自动铺丝编程算法的合理性和正确性。

[1] Shirinzadeh B,Cassidy G,Oetomo D,et al.Trajectory generation for open-contoured structures in robotic fiber placement[J].Robotics and Computer-Integrated Manufacturing,2007,23(4):380-394.

[2] 肖军,李勇,李建龙.自动铺放技术在大型飞机复合材料构件制造中的应用[J].航空制造技术,2008(1):50-53.

[3] 唐见茂.航空航天复合材料发展现状及前景[J].航天器环境工程,2013,30(4):352-359.

[4] 肖军,李勇,文立伟,等.树脂基复合材料自动铺放技术进展[J].中国材料进展,2009,28(6):28-32.

[5] 梁宪珠,张铖.浅谈降低国内航空复合材料结构成本的途径[J].航空制造技术,2011(3):40-44.

[6] 朱晋生,王卓,欧峰.先进复合材料在航空航天领域的应用[J].新技术工艺,2012(9):76-79.

[7] Tang Jianmao,Stephen K L Lee.Recent progress of applications of advanced composite materials in aerospace industry[J].Spacecraft Environment Engineering,2010,27(5):552-557.

[8] 林胜.自动铺带机/铺丝机(ATL/AFP)—现代大型飞机制造的关键设备(上)[J].世界制造技术与装备市场,2009 (4):84-89.

[9] 林胜.自动铺带机/铺丝机(ATL/AFP)—现代大型飞机制造的关键设备(中)[J].世界制造技术与装备市场,2009 (5):89-95.

[10] 林胜.自动铺带机/铺丝机(ATL/AFP)—现代大型飞机制造的关键设备(下)[J].世界制造技术与装备市场,2009 (6):78-83.

[11] 富宏亚,韩振宇,路华.纤维缠绕/铺带/铺丝成型设备的发展状况[J].航空制造技术,2009 (22):43-46.

[12] 张振甫,肖军,吴海桥,等.复合材料锥壳0°铺层的自动铺放成型方法研究[J].宇航材料工艺,2007 (2):55-57.

[13] 卢敏,周来水,王小平,等.圆筒状构件的多层铺丝路径生成算法[J].航空学报,2011,32(1):181-186.

[14] 韩振宇,李玥华,富宏亚,等.锥壳零件自动铺丝变角度轨迹规划算法[J].计算机辅助设计与图形学学报,2012,24(3):400-405.

[15] Blom A W,Lopes C S,Kromwijk P J,et al.A theoretical model to study the influence of tow-drop areas on the stiffness and strength of variable-stiffness laminates[J].Journal of Composite Materials,2009,43(5):403-425.

[16] Blom A W,Abdalla M M,Gurdal Z.Optimization of course locations in fiber-placed panels for general fiber angle distributions[J].Compositions Science and Technology,2010,70(4):564-570.

[17] Blom A W.Structural performance of fiber-placed,variable-stiffness composite conical and cylindrical shells[D].Delft:Delft University of Technology.Faculty of Aerospace Engineering,2010.

[18] 裴志军.砼搅拌运输车搅拌筒对数螺旋线螺距的探讨[J].专用汽车,2006(6):28-31.

[19] 熊文磊.基于网格化曲面的自动铺丝轨迹规划研究[D].南京:南京航空航天大学,2012.

[20] 李俊斐.基于结构设计的开孔曲面自调节铺丝轨迹规划算法研究[D].南京:南京航空航天大学,2013.

[21] 梅向明,黄敬之.微分几何[M].北京:高等教育出版社,2005:145-146.

[22] 樊真美.圆锥对数螺线的性质[J].南京师范专科学校学报,1999(3):15-19.

(编辑：薛永利)

Automated fiber placement for circumferential programming method of conical shell and placement processing property

WEN Li-wei，HUANG Wei，WANG Xian-feng，XIAO Jun

(College of Material Science and Technology，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

In order to solve the problem of automated fiber placement(AFP)circumferential programming for composite conical shell,a new method of trajectory planning based on the conical pitch was presented.Through the analysis of the relationship between the helix angle and the pitch of the cone,the helix angle was changed to keep the pitch constant so that the placement process could be operated smoothly without gaps，overlaps and variation of prepreg.A simple programming method for small cone angle was given.And the manufacturability for this programming method was analyzed by comparing the maximum deflection angle of geodesic trajectory placement angle and fixed angle trajectory with this programming placement angle.The maximum geodesic curvature of trajectory of this programming method was estimated.The programming method was validated using AFP to lay down a tail cone of a fuselage.Results show that this programming method is effective for controlling the AFP process.

composite materials；automated fiber placement；trajectory planning；cone；manufacturability

2015-09-16；

2015-11-13。

大型复合材料预制件铺放中纤维形态形成机制与精准调控原理(973项目：2014CB046501)

文立伟(1970—)，男，博士/副教授，主要从事复合材料自动铺放控制方面的研究。

黄威(1990—)，男，硕士生，主要从事复合材料自动铺放成型方面的研究。E-mail：hw0618@126.com

V261.97

A

1006-2793(2016)06-0815-05

10.7673/j.issn.1006-2793.2016.06.014