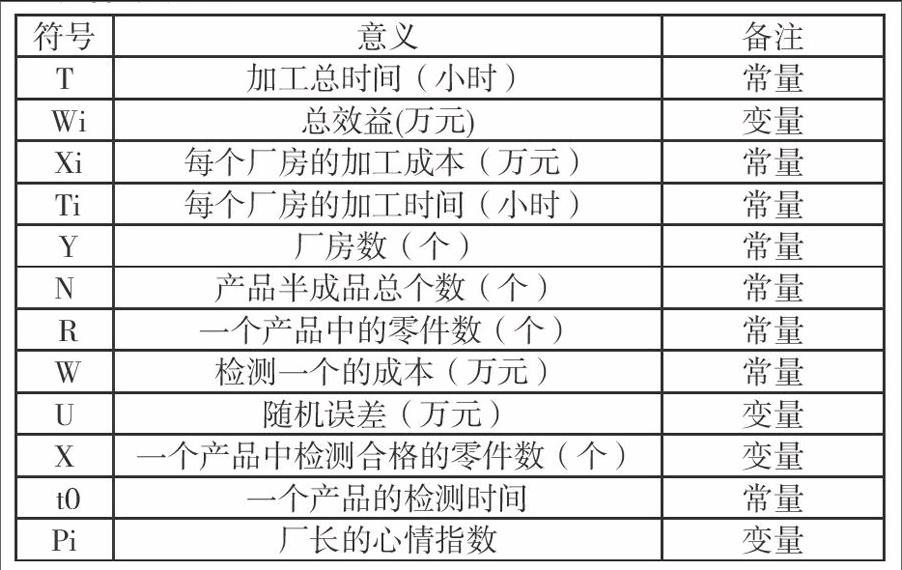
决策方案中的成本与结果的平衡问题
刘乐然
摘要:当面临多个选择时,人们往往需要进行决策。在可以自主选择的前提下,决策通常是根据个人对事物的分析、判断和兴趣来作出决定。两种极端的决策准则是:
“决策的结果最好”和“决策的成本最小”。在做决策的时候,这两种准则都需顾及,但事实上两者往往并非是简单的正比关系,即结果最好未必意味着成本最小。这两者之间的关系还需我们调和,以优化决策。
围绕实际问题中的成本与利润的平衡,本文由工厂零件的加工模型入手,探讨决策成本与决策结果的平衡关系。
本文分为四个部分,首先,建立工厂的实际背景,对零件加工的情况进行概述;其次,对该模型中决策成本与结果的表现进行分析;接着,针对其中的不确定因素进行探讨与控制;最后,通过数学方法对该模型的鲁棒性进行检测。
关键词:数学建模;概率分布;回归分析
一、背景构建
1.厂长同学的加工厂开业啦!他从外地购买了一些半成品但苦于难以区分其优劣程度,每台机器中有许许多多不同的零件,为此他向hey老板购进检测机器。检测机器需要花费一定的时间金钱判断零件是否损坏,从而判断半成品等级,而等级又决定了将来加工成成品需要的时间金钱及将带来的利润,于是为了获取最大利润他不得不冒风险进行处理,请运用数学建模的知识,围绕检查零件及加工过程,设计加工参数,对该问题进行优化使得厂长同学获取更多利润。
二、问题的提出
给定该工厂的标准产品为n个零件,检测和生产的时间分配需要由厂长决定。由于总时间有限,厂长同学只能尽量找到最优的时间成本安排
由于工件的合格性检验是简单随机抽样,因此不可避免的会与实际抽样产生误差,选择适当的数学公式,探讨如何预测并控制该误差。
不同的工件由于等级不同会有不同的受欢迎程度,产生不同的效益,同时它们的生产成本也各不相同。
综合以上三点,我们需建立描述工件生产的利润模型,并在此基础上讨论如何平衡结果与成本的关系。三、模型假设
(1)假设所有的工件标准都是真实的
(2)假设工件的定价是已知的
(3)假设零件的测量精度范围为已知
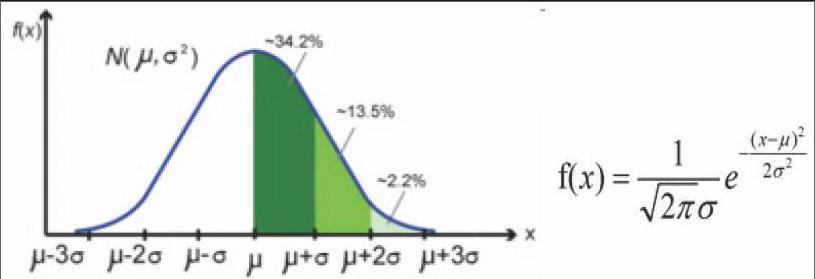
(4)假设工件的等级对于厂长同学是未知的,而实际上根据零件损坏的个数近似成正态分布
(5)为了与最大利益比较,我们假设规定的时间为理想状态下的设定时间。随着理想状态下零件数目变化而变化。
五、问题分析
某工厂厂房在一定时期(T)内加工一些半成品(n个),已知该批产品已经有r个零件,题目要求我们根据检测零件做出一定的判断,判断半成品的等级。但检测是需要时间和金钱的双重的成本,每检测一个零件所需时间为tl,检测一个的成本为w,检测的零件数在二分之r到r之间,这里我们设为r。利用公式得到这样的精度区间。
根据零件损坏率可以将这些产品分为不同的等级(v个),我们要根据这些等级将这些产品送入不同的y个厂房进行进一步加工成品。每个厂房加工的成本(Xi)与时间(Ti)都是不同的,效益也不同(Wi)。我们由以上的叙述得到最终的利润表达。
六、模型的建立与求解
6.1函数假设
当选择检测n个零件时,真实情况下的工件的等级是大致遵循正态分布的
Yi=11-x
由表格得到对应变量的关系,设为
Wi=f2(yi)
Xi=f3(yi)
将工件中合格零件的个数转化为标准正态分布,
即工件中平均有八个合格零件,x=8,零件分布的标准差为一个6=1。此时,f(x)表示的即为工件中有x个合格零件的概率,我们用这个概率,表示实际抽测工件得到的等级分布,并在假设无误判的前提下,得到应有的利润表示。
W0=∑f(x)*n*wi-n*w
这是理想的最大利润表述。
我们设定加工总时间为理想状态下的时间:
T=∑ti(x)*f(x)*n+n*t0
6.2模型建立
(1)目标函数
根据厂长同学的意愿,他对该批零件的等级预判的精准度可以表示为一个范围,
由于厂长同学的心情指数有变化,抽样标准也有偏差。计算机模拟时,我们将这种分布近似认为是t分布,也就是说,将心情算作偶然误差,并将以上的精确度区间记为E={1-& 将区间E改动到图示范围内,并随机模拟给出厂长同学今天的心情指数。 (2)约束条件 由于我们只能得到一个置信区间,因此,不妨将这个置信区间所对应的概率记为pi即正态分布所对应的区间。厂长同学根据心情得到的结论可由t分布得出,记心情指数为t并由此得到一个函数,以(-&,&)为标准,则工件检验的零件数为n0=n+t。 6.3模型解决 6.3.1修改以上的公式为 Wi=pi*(∑f(x)*n*wi-n*w); 并计算出最终的利润曲线比较得到最大值 七、模型的评价与改进 7.1模型评价 优点决策成本的表示,由于题目中alphago与李世石的决战中,alphago的决策主要分为择优筛选、行棋,两者配比在一定程度上决定了决策的优化程度。我们使用费用作为衡量标准,将决策的成本与决策实施所需成本分别用两个互相关联的量来表示。其中随机成本的引入,使得问题不失实际性与随机性,厂长的心情作为主观因素,根据统计知识变为可操作的量。 本文建立了对于该问题的回归分析,并可以计算出实际情况对应的常数。见附录。 缺点:本文建立心情指数这一变量,目的是描述操作人员的主观判断引起的误差,并使用t分布来拟合这一变化。而实际情况中,由于人员主观失误误判的偏差情况极为复杂,应该进行更为广泛的研究调查得出结论。 7.2模型改进 另外,我们在建模的时候,忽略了政府的宏观调控对价格的影响,而是简单地将工件数量理想化。但事实上,工厂每个月能购买到的工件数量也不一定是充足的,因此每月购买的工件数也是一个动态变量,模型的改进也要考虑政策的影响。模型的进一步优化也包括考虑周期成本以及政府政策在其中起到的不确定性影响。应该根据实际数据,进行曲线拟合,得到可靠的回归方程。 问题一中,我们设立了零件的等级抽测背景,将决策成本、实施成本、决策结果剥离看待,利用时间金钱进行限制。并充分考虑抽样误差,根据正态分布、t分布进行模型建立;并得到了检测中主观因素对结果的影响。进行共线性检测,得到所得函数系数的精确度,对模型进行优化; 八、结语 在生活中我们会遇到丰富的选择,选择的过程的实质即为决策问题的处理。我们处理决策问题不仅需要考虑优化决策的结果,还需要关注决策的成本。我们的目标即为平衡和调和两者的关系。下面我们将借助具体事例分析两种关系的平衡以及如何决策的问题,并试图将问题推广到更加一般的情形,为解决一般的决策问题来提供帮助。