关于三簇新的Evans三角形

李永利

(河南质量工程职业学院 467000)

1977年，R.Evans在《美国数学月刊》上提出一个未决问题[1]：“求出所有的整数边三角形,使它的某个高与底边之比为整数.”此问题称为Evans问题，被Richard K.Guy收录在《数论中未解决的问题》一书中.文[2]指出这个比不能为1和2，但可以为3，并提出问题：这个比能否为大于3的整数？

定义1某个高与底边之比为整数的整数边三角形称为Evans三角形，并称三边长互素的Evans三角形为本原Evans三角形.

定义2Evans三角形中是整数的高与底边之比称为该Evans三角形的Evans比.

约定：a,b,c表示△ABC的三边长，rc表示c边上的高hc与c边长之比.

2000年以来，Evans问题引起国内众多学者的关注与探究，得到一些有价值的结果.最近，张敬坤老师在文[3]中给出Evans三角形的一个充要条件，得到

命题[3]设n为正整数，则n是某个Evans三角形的Evans比，当且仅当存在正整数x,y，使得y2=x2(x+1)2-x(x+1)n2(1)

其三边长满足

本文将给出不定方程(1)的三种类型的解，由此可构造出三簇新的Evans三角形.为此，先给出函数f(t)=2t2-1有关迭代的一个引理.

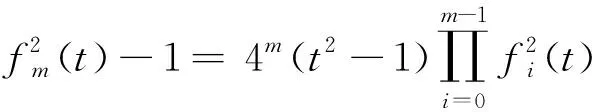
(3)

证明用数学归纳法.

1)当m=1时，

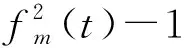
=f2(t)-1

=[f(t)+1]·[f(t)-1]

=2t2·(2t2-2)

=4t2(t2-1)，

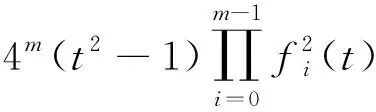
=4(t2-1)t2

=4t2(t2-1)，

所以，当m=1时(3)式成立.

2)假设当m=k(其中k为正整数)时(3)式成立，即

则当m=k+1时，有

=[f(fk(t))+1]·[f(fk(t))-1]

所以，(3)式当m=k+1时也成立.

由1)，2)的证明可知，(3)式对一切正整数m均成立.引理证毕.

注：显然f1(t)=f(t)，fm(t)是f(t)的m-1次迭代函数.

例1设m为正整数，函数f(t)=2t2-1，定义fi(t)=f(fi-1(t))，其中i=1,2,…,m，并记f0(t)=t，pk=k2-1，k为大于1的整数，令

则由引理可知

可验证n,x,y满足(1)式，由(2)式可得Evans三角形的三边长为

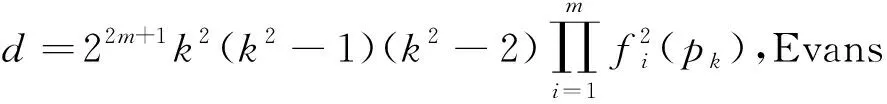
(5)

其Evans比为

(6)

例2设m为正整数，函数f(t)=2t2-1，定义fi(t)=f(fi-1(t))，其中i=1,2,…,m，并记f0(t)=t，qk=2k2-1，k为大于1的整数，令

则由引理可知

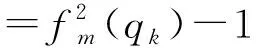
可验证n,x,y满足(1)式，由(2)式可得Evans三角形的三边长为

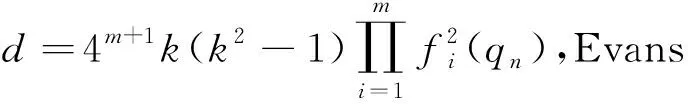
其Evans比为

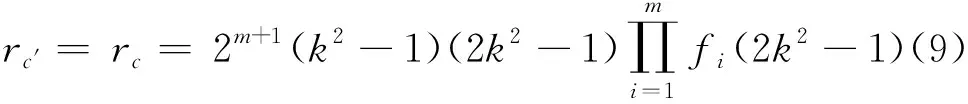
例3设m为正整数，函数f(t)=2t2-1，定义fi(t)=f(fi-1(t))，其中i=1,2,…,m，并记f0(t)=t，lk=k4-3k2+1，k为大于1的整数，令

则由引理可知

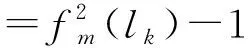
可验证n,x,y满足(1)式，由(2)式可得Evans三角形的三边长为

其中

其各边长同除以公因子d，得到与其相似的Evans三角形，其三边长为

其Evans比为

(12)

注1在例1中，取m=1，可得Evans比为[4]

rc=4k(k2-2)(2k4-4k2+1)的Evans三角形.

注2在例2中，取m=1，可得Evans比为[5][6]

rc=4(k2-1)(2k2-1)(8k4-8k2+1)

的Evans三角形.

注3在例3中，取m=1，可得Evans比为

rc=4k(k2-1)(k2-2)(k2-3)[2(k4-3k2+1)2-1]

的Evans三角形.

注4可以证明，例1和例3中得到的Evans三角形均为本原Evans三角形，例2中得到的Evans三角形当k为偶数时为本原Evans三角形，证明从略.

Evans三角形的求解问题，归结为求三元不定方程(1)的正整数解问题.本文给出的(4)、(7)、(10)三式 ，分别是不定方程(1)的三簇类型的正整数解.当正整数m或k取定值时，由这三簇解可得到无穷多类新的Evans三角形.如何求出不定方程(1)的所有正整数解，有待进一步探究.