经典NIM游戏的变式及NIM型游戏(续)

王姿婷 李建华

(1.海南省文昌中学 571300；2.北京师范大学数学科学学院 数学与复杂系统教育部重点实验室 100875)

3.2 威索夫游戏

游戏介绍：

威索夫(W.A.Wythoff)游戏⑥是一种重要的组合游戏形式，其规则为：两人轮流从甲乙两堆棋子中移走一些棋子，移走棋子的方式可以以下方式中的一种：

1.从任意一堆中移走不少于1颗的棋子；

2.从甲乙两堆棋子中同时移走相同数目(不少于1颗)的棋子；

游戏的目标是：谁移走最后一颗棋子谁就可以获胜.

游戏中的数学：

很明显，这与两堆的经典NIM游戏已有很大不同，由于这一游戏能够从两堆中同时取走相同数目的棋子，故原先两堆相等的状态不再是平衡的了，因为这种局势下能够在一次拿取后又回来，因此并不能稳固地由一方控制.若我们假定两堆的棋子的数目分别是p颗和q颗，从后继局势的角度来考虑，会发现先手在两堆石子(p,q)中(不妨总设为p≤q)的取法似乎有很多种，又由于每一方都不知道对方会如何取棋子，故局面变数似乎挺大的，但真的只能走一步算一步吗？

可知，(3,5)和(1,2)一样，也是后手有利的局势.于是现在又可以排除掉(3,p)、(5,p)以及除(3,5)外两堆棋子数差值为2的局势了，接下来可以考虑差值为3的，先前还未排除过含有4的局势，故现在可以考虑分析(4,7)

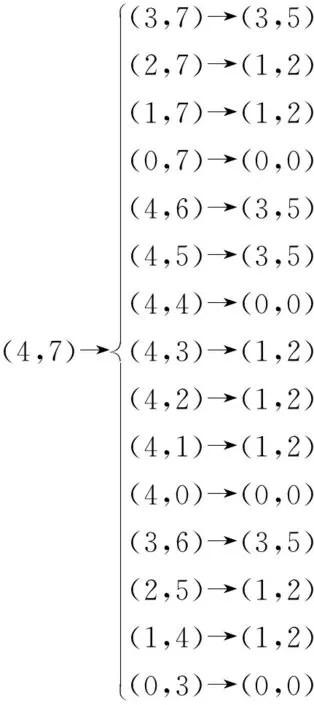
经过不多次的试探，我们可以很快发现，(1,2)，(3,5)，(4,7)，(6,10)，…都是后手有利的局势.当然，随着棋子数目的逐渐增多，后继局势的数量会迅速增加，一直这样分析其后继局势显然不现实.不过我们现在可以回过头看看我们手头已经有的东西.

我们容易发现，从两堆棋子颗数差值的角度确实能够收有成效，另外我们在确定一个后手有利的局势之后能够排除掉一些数字已使用过的局势，然后由未使用过的数字及差值能够构造出新的局势，往往这个局势就是一个后手有利的局势.下面我们可以尝试检验我们这一想法：

我们假设差值为小于k的后手有利的局势已得出，且尚未被使用过的数字为s，下面我们验证(s,s+k)也是一个后手有利的局势.

首先分类讨论先手可能做出的拿取操作：

1.若先手从两堆中同时拿取若干棋子，使其变为(t,t+k)，注意到，由于t

2.若先手在堆数为s的棋子中进行拿取，使其变为(t,s+k)，由于此时两堆棋子的数目大于k并不是已找出的后手有利状态，且t

3.若先手在堆数为s+k的棋子中进行拿取，使其变为(s,w)，若此时的ws，那么由于w

检验完毕.

借用归纳假设，我们知道，前面观察得到的寻找后手有利的局势的方法确实能够帮我们由小到大遍历出所有的后手有利的局势！而且能够知道，这些后手有利的局势能够稳固地由后手控制，因此正是我们找寻的制胜关键局势！

3.3 皇后登山游戏

游戏介绍：

“皇后登山”游戏是由 Rufus Isaacs 在 1960 年左右提出来的[注]Wythoff's game at Cut-the-knot.与前面介绍的取子游戏不同，这一游戏是将目标棋子按约定的方式进行移动，移动到目标位置即算成功.具体的规则是：在下图7所示的有18×18=324个小的正方形格子的围棋盘中，将在右上顶角处的格子设为目标位置，并用“ ▲” 这个符号标记，代表山顶.游戏双方分别为A和B：首先，第一个游戏者A，把一位“皇后”(可以是一枚棋子或其他小物件)放在棋盘的最下面一行或最左边一列的某个格子里(见灰色区域)，放好后就可以轮到B走了，之后两人轮流决策，决策规则是：“皇后”只能向上、向右或向右上方(45度方向)斜着走，每次可以走的格数不限，但不得倒退，也不能不走；谁先把“皇后”移进目标位置即标有“▲ ”的山顶位置就算获胜.

图7

游戏中的数学：

上述规则其实相当于给定目标位置后就确定了上与右两个正方向作为前进的方向，并允许斜向的前进方式，而移动的规则相当于规定整个过程不能后退或停滞不前，以“皇后”所在的位置作为左下角直指山顶所形成的线为对角线的矩形就是下一步“皇后”尚有可能移动到的范围，随着游戏的进行，这样的矩形会越来越小，直至成为长或宽为1的矩形时，下一位玩家就可将其移至山顶，当然，若其间此矩形成了正方形，也即某一方使“皇后”恰好放置于45度方向能直指山顶的位置时，下一方亦可直接到达山顶.于是我们不妨现在简化版的小棋盘上进行分析，如图8.而刚刚分析到的危险位置我们就可以用阴影部分将其呈现出来.

图8

显然，如果对手不慎把“皇后”走进图8中带阴影的格子里，由规则我们就知道，接下来，我们只需要一步就能够把“皇后”移动至到山顶而获胜，因此，任何一方都应该避免将“皇后”移动到这些危险位置也即有阴影的格子里，而且应该尽可能地压制住对手，迫使他不得不把“皇后”走到有阴影的格子里去.而这一点，某些特殊位置似乎是可以办到的.

例如，细心的读者可以从图8中看出，如果我方能设法将“皇后”移动至标号为①或②的格子里，那么对手就只能把“皇后”移动进有阴影的格子里了；换句话说，只要占领了①或②，且以后的走法得当，就必稳操胜券.所以①和②这两个关键位置的意义，像极了军事上的“制高点”[注]倪进，朱明书.数学与智力游戏[M].大连：大连理工大学出版社，2008.4.pp. 135-149.，一旦占据便可居高临下，一夫当关.

可是，怎样做才能占领①或②呢？这时候相当于将原先抢占山顶的问题化归为了抢占①或②这两个位置，它们便变成了新的“山顶”，同样的分析原理，如果对手把“皇后”走进有虚线的方格里，则我方就能在下一步占领①或②，从而最终获胜，参看图9.那么，怎么样迫使对方不得不把“皇后”走进有虚线的方格呢？于是我们又将问题化归为占领③或④这对关键位置的任一格了！

图9

我们能够知道，只要棋盘足够大且对称，这样的关键位置总是成对出现的，而且耐心的话总可以能一对一对的找出来.所以我们只需要继续运用上述分析方法进行递推，就可以最终得到本游戏中18×18的围棋盘上的全部关键位置，结果参看图10.

从图10中我们可以看到，若给由各个关键位置出发的横纵斜三线画上虚线，可以看到，所有的虚线将整个棋盘的格点无一遗漏地覆盖上了！并且，从关键位置的特点，我们可以看出，一旦我们占据了某一个关键位置，这一关键位置的上方右方还有斜前方都不会有另一关键位置，故在下一步的操作中，对方必无法达到另一个关键位置，即我们这些关键位置具有“对位于关键位置的“皇后”进行任一操作均会离开关键位置”这一性质，并且，对方无论在下一步中将“皇后”移动到了哪里，我们必能找到其对应的另一个关键位置，因为所有的虚线将棋盘覆盖遍了，那么无论“皇后”落在哪一条虚线上，末端总是指向这条虚线的出发点——关键位置上的！也就是说这些关键位置还具有的“对于任一偏离关键位置的“皇后”，先手总能找到办法使其回到关键位置上”这一性质！这两点恰好满足了我们对制胜策略的要求.

综上，我们所要做的就是寻找棋盘上的这些关键位置！

图10

现在我们试着将刚刚的倒推分析用代数的方式呈现出来.若将关键位置放在笛卡尔坐标系下刻画(由于这些关键位置总是成对且对称出现的，故在对称意义下的不妨只取每对中斜下方的那个作为代表，即横坐标不大于纵坐标的那个).现取山顶为坐标原点倒着分析，即将下与左分别为正方向，单位长度就自然取为每个相邻方格中心的距离，并将所有的关键位置所对应的坐标按自然数大小的顺序排列，即可得到如下的六个点：

A1(1,2),A2(3,5),A3(4,7),A4(6,10),A5(8,13),A6(9,15).

若对前面提过的游戏有所了解的话，会发现，这些关键位置所对应的坐标数对，恰好是威索夫游戏中的平衡状态！这其实很好理解，将棋盘中的位置与坐标系中的点建立对应后，可以发现横向和纵向的操作会使横坐标或纵坐标减小，这其实就对应着威索夫游戏中在一堆中取子的操作，45度方向的斜向的操作会使横纵坐标同时减小相同数目，这正好对应威索夫游戏中在两堆棋子中拿取相同数目棋子的操作，也就是说，这个游戏同威索夫游戏是貌异实同的，于是这一游戏的制胜策略便可化归为威索夫游戏策略解决问题了.

3.5 斐波那契型的NIM游戏

游戏介绍：

此游戏[注]EP8:Fibonacci Nim(斐波那契取石子博弈)与经典NIM游戏一样都是取棋子游戏，不过它只有一堆棋子，而游戏的规则是：有一堆棋子n颗，两人轮流取走棋子，拿取方法为：

1.开局后的第一次取棋子不能一次取完；

2.每次至少取走一颗棋子；

3.每次取的棋子数不能超过上一个人取得棋子数的二倍.

4.谁将最后一颗棋子取走谁就胜利.

相对于经典NIM游戏每次取棋子数目任意这一点来说，这一游戏中后一玩家受前一个玩家的影响明显要大得多，似乎每一轮游戏中的不确定因素会更大一些，因为保不准前一个玩家会取走多少，而这一数目的两倍却是后一个玩家的上限.

游戏中的数学：

我们首先从较小的n开始尝试：

当n=2时，先手只能取走一颗，后手即可取完，先手必败！

当n=3时，先手只能取走一颗或两颗，而无论是哪一种情况，后手都可以取完，故先手必败！

当n=4时，为了不让后手取完，先手第一次只能取走1颗(否则后手能在其取棋子的两倍内将剩余棋子取完)剩下n=3的情况给后手，如之前分析，这种情况下是先手必胜！

当n=5时，同样的，先手第一次也只能取走1颗，剩下n=4的情况，故这种情况下先手也只能接受必败的结果！

当n=6时，由于取到两颗及以上时后手会将剩余棋子取空，故先手只能取1颗棋子，剩下5颗，同上分析，先手必胜！

当n=7时，为避免后手一次取空，先手至多取2颗棋子.先手若取走1颗棋子剩下6颗，则其必胜！若先手取走2颗棋子，剩下5颗，则先手势必会失利！当然，先手肯定不会选择后者，故此情况下先手必胜！

当n=8时，先手若取走1颗棋子剩下7颗，则后手必会取走2颗剩下5颗，使得先手必败！先手若取走2颗棋子剩下6颗，则后手必会取走1颗剩下5颗，同样是先手必败！而若先手取走3颗及以上的棋子，势必会造成后手将剩余棋子取空的败局.

当n=9时，同理分析，先手第一次最多取走2颗棋子，先手若取走1颗棋子剩下8颗，则后手只能取走1颗或者2颗而剩下7颗或者6颗，于是先手便可再取走1颗剩下5颗，使得先手必胜！而先手若取走2颗棋子剩下7颗，则后手必会取走2颗剩下5颗，那么后手就可获胜！当然，由先手先选择的话势必会选择先取走1颗，故此情况亦为先手必胜！

当n=10时，先手初次可选择拿走1至3颗，也就是剩下9或8或7颗，但由之前分析过8颗是先手必败局面可知，故此时拿走2颗剩下8颗方为明智之选.所以此情况亦为先手必胜！

当n=11时，先手初次亦可选择拿走1至3颗，也就是剩下10或9或8颗，同样，由之前的分析可知，此时拿走3颗剩下8颗则必胜.故此情况亦为先手必胜！

当n=12时，先手初次可选择拿走1至3颗，也就是剩下11或10或9颗，由于剩下10颗或9颗时，后手可立刻拿取至剩余8颗而占据优势，故先手必须绕开这两种情况而选择剩下11颗，那么后手就只能拿走1或2颗，也就是剩下10颗或9颗，这正好可以使得先手能够顺势拿取至8颗继而取胜.故此情况先手必胜！

当n=13时，此时先手初次最多颗取走4颗，也即可剩下12颗11或10或9颗，由于剩下11颗、10颗或9颗时，后手均可拿取至剩下8颗，故先手势必会选择拿取1颗剩下12颗，那么后手只能选择拿取1或2颗，也就是剩下11颗或者10颗，若剩下10颗，那么先手就可以拿取至剩下8颗， 当然后手绝不会做此选择，只会选择拿走1颗剩下11颗，那么先手只能拿至10或9颗，遂后手便可拿至剩余8颗！故此情况先手必败！

……

通过上面的尝试，我们能够发现，存在着若干的“先手必败点”及“先手必胜点”，我们可以先看“先手必胜点”，它们是4，6，7，9，10，11，12这些，直接看上去似乎并没有太多特点.那我们可以试着看看“先手必败点”，一旦遇到这样的局面，先手稳输，而这些状态是2，3，5，8，13这些，而这一串数字很容易观察出它们是有规律的，那就是从第三个数开始，每个数都是前两个数字之和，这也刚好是斐波那契数列！虽然会花费一些时间进行分析，但只要耐心，我们不难验证，21、34恰好也是有利局势！这给了我们很大的启示！

那么，斐波那契数是否真的是先手必败的局势呢？当然，基于对平衡状态的考量，我们还需要考虑，反过来先手必败的局势是否一定是斐波那契数.下面试试证明当且仅当n为斐波那契数时，局势为先手必败的.即意味着当棋子数为斐波那契数时，先手不能一次将棋子取至剩余的另一个斐波那契数，而一个棋子数不是斐波那契数时，先手总可以在若干次拿取后率先拿到剩余一个斐波那契数.

首先，颗据斐波那契数列的性质，我们有：

f(k)=f(k-1)+f(k-2)=2f(k-2)+f(k-3)

且观察易知，k>5时，则有f(k-2)-f(k-3)>1，因而

向上取整即有

故有

即在当前局势是斐波那契数的情形下，先手无论怎么取，都不可能一次将棋子取至剩余的另一个斐波那契数！

另外，对于n较小的情况，我们不经几次尝试就可以发现，若n不是一个斐波那契数，则先手总可以率先取到下一个斐波那契数.下面我们假设当棋子数小于n时这种状况都成立，我们接下来分类讨论一下n的所有可能情况：

1)当前可以直接取走若干棋子，使得剩下的棋子数为一个斐波那契数.

显然，此时先手能够率先取到斐波那契数.

2)当前的局势在一次取棋子的操作中无论怎么取棋子，剩下的棋子数都不是一个斐波那契数.

不妨设f(k)

A)若m不是一个斐波那契数，则问题转化为，经过若干轮后，谁恰好能将这m颗棋子取完造出斐波那契数f(k).而由之前的假设我们知道，m小于n，因此先手能率先将这m颗棋子取完.

B)若m是一个斐波那契数，则因为f(k)≠m≠f(k-1)因此m≤f(k-2)，于是又有：2m≤2f(k-2)

综上，在当前局势是斐波那契数的情形下，先手无论怎么取，都不可能一次将棋子取至剩余的另一个斐波那契数，当棋子数n为非斐波那契数，先手能率先将其取至斐波那契数，由此我们得出结论：对于∀n∈N，n≥2，当且仅当n为斐波那契数时，先手必败，当n不为斐波那契数时，该局势先手必胜的.而上述的这些性质恰好能使斐波那契数作为平衡状态，谁能够率先给对方留下斐波那契数的局面，谁将最终获胜.

至此，我们已经借用几个游戏将经典NIM游戏通过调整规则可得的这一类变式游戏进行了举例.通过对经典NIM游戏以及穆尔游戏、威索夫游戏、斐波那契型NIM游戏等的介绍，我们可以发现，这些游戏都有着异曲同工的制胜规律，可谓“貌离神合”.

容易知道，经典NIM游戏的两类变式游戏，其制胜规律本质都在于某方对有利局势的牢固控制，若一方能够每次都占据有利局势并且留给对方不利局势的话，该方必能够稳操胜券，从这个角度来看，这些游戏从策略上看都是有着很强的相似性的.由此，我们完全可以给出一个基于上述所提及游戏找出的策略，总结出更广义的游戏类型——NIM型游戏.而在两类变式游戏描述中，都提到了平衡数组、后手有利的局势等这些关键状态，为了说明的完整性，我们有必要对这样的状态进行说明.故在定义NIM型游戏之前，我们先给出平衡状态的一般性定义：

在一个二人轮流进行决策游戏中，若存在这么一类游戏状态，能够满足下面几种条件，我们就称其为平衡状态：

1.该状态是在游戏规则下的可行操作中能够出现的；

2.游戏中，一旦游戏的某一方(记为A)在决策中达到了该状态，那么另一方(记为B)接下来无论如何决策都势必要破坏这种状态；

3.当该状态被之后的决策破坏后，必存在某种策略能够保证，继续游戏时，这样的状态必能率先回到A的手中.

在存在平衡状态的游戏中，不满足上述条件的游戏状态则称为非平衡状态.

由定义我们知道，平衡状态的判定主要有两点，一个是“他人必破坏”，简称为“必破性”，一个是“自己必能还原”，简称为“还原性”，而且平衡状态完全是可操控的、稳定由一方牵制的游戏局面，根据平衡状态这一策略特征，我们便可以对满足策略符合这些特征的游戏进行定义了.下面，我们给出NIM型游戏的定义：

1.在预定好的游戏规则下，游戏中的双方轮流进行决策，不能在有决策空间时选择不实施任何操作；

2.在无法进行决策时游戏结束并分出胜负；

3.每次决策只针对当前局面进行，不可有回退操作；

4.游戏中存在平衡状态.

若某一个多人游戏能够满足以上四种条件，这个游戏就是一个NIM型游戏.

NIM型游戏抛开了游戏本身的规则设定、游戏道具等方面的限制，它的关注点是游戏中是否存在一些特殊的状态——平衡状态，并在得到肯定结论后进一步将平衡状态分析清楚.这样一来，许多看似无直接联系的游戏都能够纳入这类体系中了.

需要说明的是，包括罗见今老师在内的许多数学工作者对NIM型游戏的定义等已进行过一些讨论，这并不是一个全新的概念，此处的定义是笔者对经典NIM游戏及其变式呈现出的内在本质关联，所进行的一些自然的思考与总结.

先前文章中所提到的平衡数组、后手有利的局势等都是平衡状态，事实上，在双人决策游戏中，平衡状态又可根据优势方分为两种，即先手有利的平衡状态或者后手有利的平衡状态.

NIM型游戏不仅乐趣横生，而且处处体现着数学的美妙，让人啧啧称奇.而判定一款游戏是否归为NIM型游戏，关键在于对其是否具有平衡状态这一条件的判定，也就是对游戏状态中“必破性”与“还原性”的证明.NIM型游戏的一般性定义使得它可囊括一大类满足上述特点的游戏，它关注到了游戏结构及策略特点而非停留在游戏形式上，为之后一些系统性的整理工作带来便利.

4 结束语

在第一种类型的变式游戏中，变式的味道较浓，其本质无非是将经典NIM游戏的游戏形式用另外的方式进行表达处理，例如棋子堆数变成了可操作棋子的个数，而每堆棋子的数目变成了相应棋子的关键行棋步数，可以说，为经典NIM游戏量体后裁了衣裳，稍加修饰后再进行呈现.虽说将原理进行对应后，熟悉经典NIM游戏的玩家就能够轻易地按照制胜策略进行决策了，但正是建立对应及进行转换这一举足轻重的处理措施，并非想象的那样可以轻松被考虑到，因为那需要对经典NIM游戏有较多的了解与较深的理解，而现实中玩家或是学生往往是只见树木不见森林的，会被所进行的游戏本身牵着走，故还是可以具备一定挑战性的.而这种游戏的变形方式可以有很多种，此处所举的例子只是其中某些变式形式，也就是说，这类型的变式游戏里面，能够有更多的变式可能，施展的空间也相当大.

第二种类型的变式游戏，是对经典NIM游戏中规则做了变动，故最后的制胜策略不简单的遵循经典NIM游戏策略，往往是背后的数学原理已经发生了较大变化从而带来制胜策略的较大调整的，这种通过增减限制来调整规则的处理方法或许能够给试图对游戏进行变式处理的学者及玩家很多尝试的启示，应用到课堂上也能有利于学生思维能力的培养.

通过这两类变式游戏的介绍，可以发现经典NIM游戏策略给出后，这条由“游戏皇后”开辟出的道路没有走到尽头，反而同树木一般，不断在各种方向上生长出枝蔓，编织出一个充满智趣的世界.或许，这正是研究NIM型游戏的乐趣之一，能够与各种美好不期而遇.