两类偶特征有限域上的几乎完全非线性函数

张习勇， 李乃江， 鲁志波, 李德全

(1.天地一体化信息技术国家重点实验室 北京 100020； 2.解放军信息工程大学 河南 郑州 450001)



两类偶特征有限域上的几乎完全非线性函数

张习勇1,2， 李乃江1,2， 鲁志波1, 李德全2

(1.天地一体化信息技术国家重点实验室 北京 100020； 2.解放军信息工程大学 河南 郑州 450001)

密码学中所涉及的函数包括布尔函数和向量值函数，这两类函数的安全性指标包括差分一致性和非线性度等.构造密码学性质良好的低差分一致性函数是密码学中的热点问题.构造了两类偶特征有限域上的、新的几乎完全非线性(almost perfect nonlinear，APN)函数，并分别证明了它们与偶特征有限域上已知的单项式APN函数EA不等价.

差分一致性； APN函数； EA等价； CCZ等价

0 引言

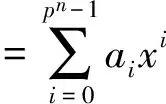
定义2 代数次数小于等于1的函数称为仿射函数，满足f(0)=0的仿射函数称为线性函数.

定义3 如果存在仿射置换A1、A2和仿射函数A使得g=A1°f°A2+A，则称GF(pn)→GF(pn)的两个函数f和g扩展仿射等价，简称EA等价.易知，EA等价的非常数函数具有相同的代数次数.文献[5]提出一种更一般的等价概念，即CCZ等价.

2005年以前，人们主要关注偶特征有限域上的单项式APN函数构造与等价归类，表1列出了偶特征有限域GF(2n)上目前已知的6类单项式APN函数，其中n为扩张次数.2006年以后，学者们相继构造出了多类偶特征有限域上，与已知的单项式APN函数不等价的多项式APN函数，文献[7]中列出了主要结果.

本文通过对偶特征有限域上已有的两类APN函数添加和式，构造了两类新的APN函数，利用反证法，通过比较等式两边对应项系数，证明了所构造的两类APN函数与表1中的6类单项式APN函数EA不等价.

表1 偶特征有限域GF(2n)上已知的单项式APN函数Tab.1 The previously known monomial APN functions over even characteristic finite fields GF(2n)

1 两类偶特征有限域上的APN函数

证明 对任意0≠a∈GF(2n)，令Δa(f(x))=f(x)+f(x+a)+f(a)，则

Δa(f(x))=ax2s+a2sx+ax2m+a2mx+u2m(a2sx2m+a2mx2s+ax2s+m+a2s+mx)+

(1)

是一个线性化多项式.

因为Δa(f(x))=0与Δa(f(ax))=0的解的个数相同，所以只需考虑等式

Δa(f(ax))=(u2m-1a2s+m+2m+u2ma2s+m+1)x2s+m+(a2m+1+u2ma2s+2m+u2m-1a2s+m+2m)x2m+

(2)

在GF(2n)中的解个数.

对等式(2)做2m次方，可得

Δa2m(f(ax))=(u1-2ma2s+1+ua2s+2m)x2s+(a2s+1+ua2s+m+1+u1-2ma2s+1)x+(a2s+m+2m+ua2s+m+1)x2s+m+

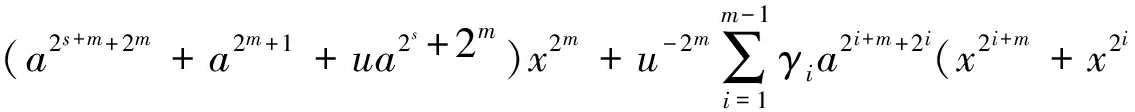
(3)

因为Dobbertin函数的Walsh谱与所有二次函数的Walsh谱均不相同[8-9]，而扩展Walsh谱是函数的CCZ等价的一个不变量，故得定理2.

定理2 定理1中的APN函数与表1中Dobbertin函数CCZ不等价.

由于CCZ等价是比EA等价更广泛的一种等价关系，可得推论1.

推论1 定理1中的APN函数与表1中Dobbertin函数EA不等价.

定理3 定理1中的APN函数f(x)与已知的单项式APN函数EA不等价.

证明 由推论1可知定理1中的APN函数f(x)与Dobbertin函数EA不等价.

因为Inverse函数、Welch函数和Niho函数的域扩张次数n只能是奇数，所以定理1中的APN函数与Inverse函数、Welch函数和Niho函数EA不等价.EA等价的必要条件是函数的代数次数相同，因而二次函数f(x)与非二次函数Kasami函数EA不等价.

(4)

由式(4)+u2m-1(4)2m可得

(5)

因为u是GF(2n)上的一个本原元，所以u2m-1≠1.

比较等式(5)两边的系数，令t为正整数，当t≠r时，有

(6)

(7)

(8)

假设存在j,使得aj≠0.如果存在k,使得bj+k-m≠0，当t≠r时，由(6)式可得

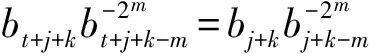
(9)

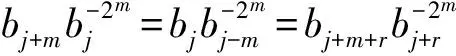
bj-m=0.

(10)

bj+r-m=0.

(11)

下面给出另外一类偶特征有限域上的与已知的单项式APN函数EA不等价的APN多项式函数.

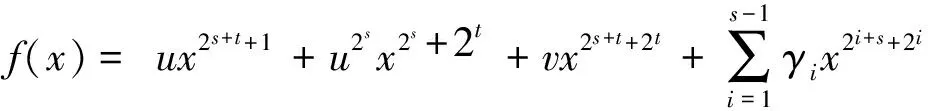
Δa(f(ax))=ua2s+t+1(x+x2s+t)+u2sa2s+2t(x2s+x2t)+va2s+t+2t(x2t+x2s+t)+

(12)

在GF(2n)中的解个数.

因为a2s+t+1是3次方元，且F2s中的元素均为3次方元，而u不是3次方元，所以ua2s+t+1∉GF(2s)，所以ua2s+t+1+u2sa2s+2t≠0.

定理5 定理4中的APN函数与Dobbertin函数CCZ不等价.

推论2 定理4中的APN函数与Dobbertin函数EA不等价.

定理6 定理4中的APN函数与已知的单项式APN函数EA不等价.

证明 由推论2可知定理4中的APN函数f(x)与Dobbertin函数EA不等价.

因为Inverse函数、Welch函数、Niho函数的域扩张次数n只能是奇数，所以定理4中的APN函数与Inverse函数、Welch函数、Niho函数EA不等价.同定理3所述，Kasami函数因为与函数f(x)的代数次数不同，所以它们EA不等价.

下面证明函数f(x)与表1中的Gold函数EA不等价.

(13)

由式(13)+(13)2s可得

(14)

因为v∈GF(22s)GF(2s)，所以v+v2s≠0，比较等式(14)两边的系数，令z为正整数，当z≠r时有:

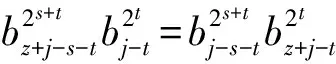
(15)

(16)

(17)

假设存在j使得aj≠0.如果存在k使得bj+k-t≠0，当z≠r时，由(15)式，可得

(18)

bj-t=0，

(19)

bj+r-t=0.

(20)

注 本文所构造的两类APN函数均为二次函数.所构造的两类APN函数与Gold函数和Dobbertin函数是CCZ不等价的.[10]

[1] 祁传达, 袁小转, 邵辉. 布尔函数的迹单项式逼近[J]. 信阳师范学院学报(自然科学版), 2014，27(3):440-443.

[2] 涂自然, 邓映蒲. 一类M-M型bent函数的代数免疫度[J]. 河南科技大学学报(自然科学版), 2010, 31(4):81-83.

[3] BIHAM E, SHAMIR A. Differential cryptanalysis of DES-like cryptosystems[J]. Journal of cryptology, 1991, 4(1):3-72.

[4] NYBERG K. Differentially uniform mappings for cryptography[J]. Lecture notes in computer science, 1994, 765:55-64.

[5] CARLET C, CHARPIN P, ZINOVIEV V. Codes, Bent functions and permutations suitable for DES-like cryptosystems[J]. Designs codes and cryptography, 1998, 15(2):125-156.

[6] BUDAGHYAN L, CARLET C, POTT A. New classes of almost bent and almost perfect nonlinear polynomials[J]. IEEE transactions on information theory, 2005, 52(3):1141-1152.

[7] BRACKEN C, BYRNE E, MARKIN N, et al. A few more quadratic APN functions[J]. Cryptography and communications, 2011, 3(1):43-53.

[8] CANTEAUT A, CHARPIN P, DOBBERTIN H. Binarym-sequences with three-valued crosscorrelation: a proof of Welch’s conjecture[J]. IEEE transactions on information theory, 2000, 46(1):4-8.

[9] NYBERG K. S-boxes and round functions with controllable linearity and differential uniformity [C]// International Workshop on Fast Software Encryption. Berlin, 1994:111-130.

[10]BRACKEN C, BYREN E, MCGUIRE G, et al. On the equivalence of quadratic APN functions[J]. Designs codes and cryptography, 2011, 61(3):261-272.

(责任编辑：方惠敏)

Two Classes of Almost Perfect Nonlinear Functions over Even Characteristic Finite Fields

ZHANG Xiyong1,2， LI Naijiang1,2， LU Zhibo1, LI Dequan2

(1.StateKeyLaboratoryofSpace-GroundIntegratedInformationTechnology,Beijing100020,China; 2.ThePLAInformationEngineeringUniversity,Zhengzhou450001,China)

Boolean function and vector function were two classes of functions involved in cryptography. It contained differential uniformity, nonlinearity, etc. as their safety indicator. Constructing low differential uniformity functions with good cryptography property was always a hot topic. Two new types of almost perfect nonlinear (APN) polynomial function over even characteristic finite fields were constructed, moreover, it was proved that the presented functions were EA-inequivalent to the previously known monomial APN functions over even characteristic finite fields.

differential uniformity; almost perfect nonlinear function; extended affine equivalence; Carlet-Charpin-Zinoviev equivalence

2016-05-03

国家自然科学基金资助项目(61572027)．

张习勇(1975—)，男，湖北武穴人，副教授，主要从事密码学研究，E-mail:xiyong.zhang@hotmail.com．

张习勇，李乃江，鲁志波,等.两类偶特征有限域上的几乎完全非线性函数[J].郑州大学学报(理学版)，2016，48(4)：1-5.

O174.4

A

1671-6841(2016)04-0001-05

10.13705/j.issn.1671-6841.2016601