基于改进遗传算法的自抗扰控制器优化设计

唐勇伟，赵景波，王茂励，郝慧娟，吕晓慧

(1. 青岛理工大学自动化工程学院，山东 青岛 266520；2. 山东省计算中心(国家超级计算济南中心)，山东 济南 250014；3. 华北电力大学电气与电子工程学院，北京 102206)



【海洋科技与装备】

基于改进遗传算法的自抗扰控制器优化设计

唐勇伟1,2，赵景波1*，王茂励2，郝慧娟2，吕晓慧3

(1. 青岛理工大学自动化工程学院，山东 青岛 266520；2. 山东省计算中心(国家超级计算济南中心)，山东 济南 250014；3. 华北电力大学电气与电子工程学院，北京 102206)

针对超空泡航行体受力特征及其航行时具有非线性、时滞与耦合等复杂问题，提出可根据适应度对控制参数进行自适应动态调整的改进遗传算法。通过建立超空泡航行体纵向模型，设计专用自抗扰控制器对其进行控制，并针对控制器参数多、调节困难的问题，改进了自适应遗传算法对其精确优化。最后通过特性仿真，验证了基于改进的自适应算法的自抗扰控制器相比经典自抗扰控制器的优势。仿真结果表明，该自抗扰控制器符合实际需求，具有良好的控制效果。

超空泡航行体；自抗扰控制器；改进自适应遗传算法；解耦；参数优化

由于海水密度较大，常规水下航行体及制导武器在水中航行时所受阻力远远高于其在空气中，因此航行速度慢且距离短，实际应用受到很大局限，必须寻求有效方法实现水下航行体的减阻提速。航行体在水下高速航行时通过气体发生器产生气化物并形成气泡将机体覆盖[1]，因此航行体受到的阻力显著降低，其运动速度得到大幅提升[2]。

然而，航行体利用空泡减阻提速，沾湿面积减小，浮力作用很大程度丧失[3]，动态性能产生极大改变，致使超空泡航行体建模和控制难度大大增加[4-5]。所以，单纯使用广泛应用于常规水下航行器控制的传统PID控制方法已不可行。自抗扰控制技术(active disturbance rejection control,ADRC)将传统控制理论的负反馈思想与现代控制的状态反馈部分思想结合，将系统内部及内外扰动等全部不确定因素视为系统的“总和扰动”，采用实时动态补偿的扰动观测和补偿控制策略，很大程度地降低了控制器对被控系统内部结构的依赖，能够有效提高系统的抗干扰能力，具有精确、稳定、鲁棒性和适应性好等特点[6-8]。本文将自抗扰控制技术应用于超空泡航行体的控制问题，提出了可根据适应度对控制参数进行自适应动态调整的改进遗传算法。

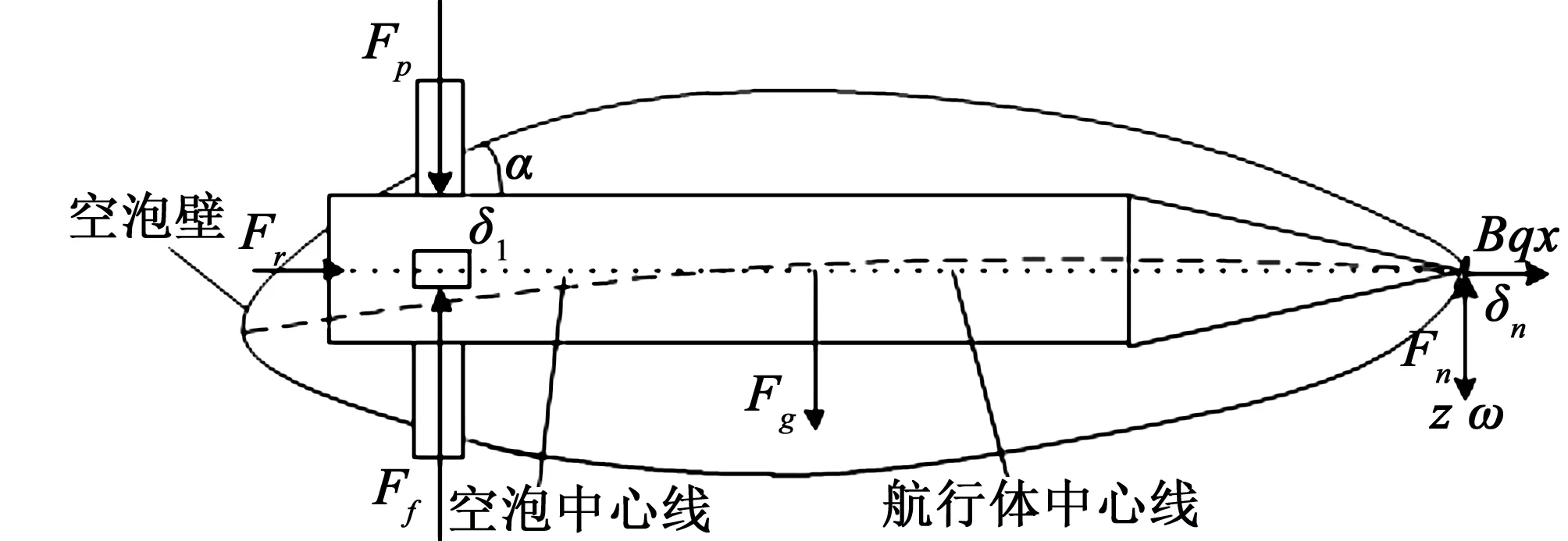
图1 超空泡航行体模型纵向受力分析图Fig.1Longitudinal force analysis diagram of supercavitation navigation vehicle model

1 超空泡航行体模型的纵向力分析

在水中运行时，航行体纵向平面的主要作用力分别为航行体质心所受到重力Fg、空化器在运行过程中受到液体流动力Fn、尾部的滑行力Fp、滑行阻力Ff和推力FT等[9]，受力相互作用，维持平衡，其纵向平面受力分析见图1。航行体模型由柱部和锥部构成，柱部长度约为锥部的两倍，模型中空化器、十字型鳍与实际相似[10]。

根据受力分析，可得其纵向运动模型：

(1)

表1 航行体模型的主要参数Table 1 System parameters of the vehicle model

将上表中各参数值应用于航行体的纵向模型后，可得系统各状态变量的系数矩阵：

(2)

2 超空泡航行体的自抗扰控制器设计

2.1 自抗扰控制器系统结构

自抗扰控制器一般包括跟踪微分器(TD)、扩张状态观测器(ESO)、非线性状态误差反馈(NLESF)三部分[6]，三者之间的有效组合，避免了对被控系统存在的非线性进行复杂的线性化处理，从而实现对非线性系统的快速、有效、无超调地有效控制，在实际工程中应用广泛。以二阶系统为对象，自抗扰控制器的系统结构图见图2。

图2 自抗扰控制器二阶系统结构图Fig.2 Second-order system structure of ADRC

其中,io(t)、O(t)、W(t)为输入、输出以及干扰信号；i1、i2都是输入信号、跟踪信号,i1是一阶导数,i2是微分；S1、S2、S3是ESO估计出的三阶状态变量；e1、e2是系统的误差量。因此，二阶的自抗扰系统包含的TD为二阶，ESO为三阶。

2.2 自抗扰解耦控制系统

超空泡航行体系统是多输入/输出被控系统，各通道之间存在着耦合作用，需将多变量的控制解耦。自抗扰控制器可以将变量间的耦合当作扰动加以估计和补偿，从而消除耦合对系统的影响[11]。以双输入/输出系统为例说明自抗扰控制下对耦合系统的解耦原理，设被控对象为：

(3)

若B可逆，则

(4)

则系统等效为：

(5)

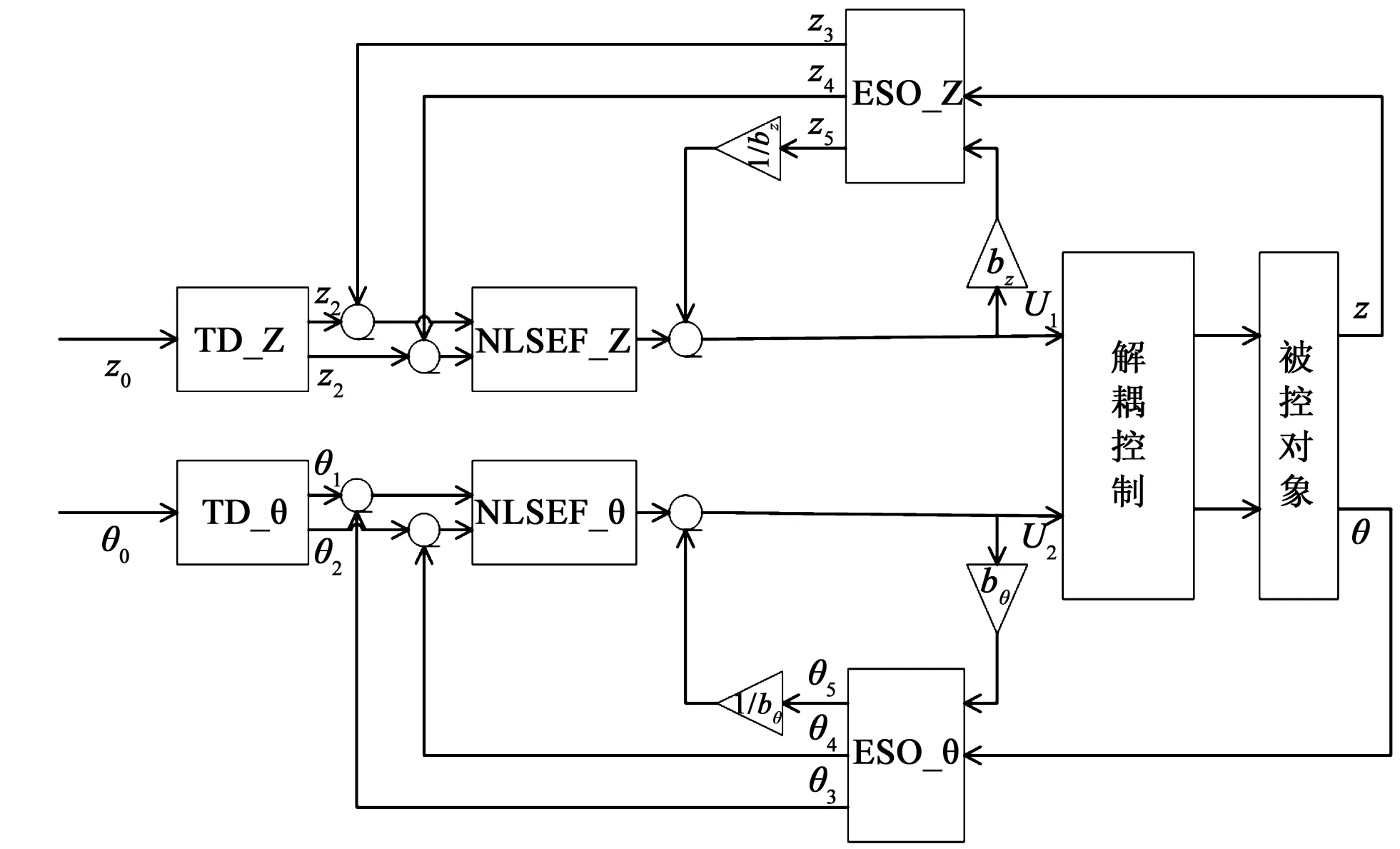
图3 超空泡航行体自抗扰控制器设计框图Fig.3 Supercavitation vehicle design diagram of ADRC

由等效公式(5)可以看出，只要ESO将各通道的a11和a22进行观测实时补偿，则系统就变为两个独立的“积分串联型”系统。对模型补偿输出量U后，根据式(4)进行逆变换，就可获得原系统式(3)的控制输入u1、u2。这样各状态变量之间的耦合关系就不再存在，在控制时就无须对系统进行动态解耦，实现了系统的解耦控制。

2.3 超空泡航行体自抗扰控制器设计

航行体的深度、纵倾在升降舵和空化器作用下同时发生变化，所以，超空泡航行体的纵向控制系统以舵偏转角δf和空化器偏转角δc为控制输入，以深度z和俯仰角θ为输出的双输入双输出系统。本文对深度TD_Z、ESO_Z、NLSEF_Z以及纵倾TD_θ，ESO_θ、NLSEF_θ三部分的离散算法进行改进，并研究适用于超空泡航行体的自抗扰控制器，原理图见图3。

3 改进算法的自抗扰控制器优化设计

自抗扰控制器中r、h、α1、α2、δ等11个参数需整定[12]。本文将自抗扰控制器设计问题转化为一种参数寻优问题，以解决目前参数调整在人工调试过程中选取调试方法及参数修改存在的很大程度的不确定性。

3.1 改进的自适应遗传算法

遗传算法中有选择算法和交叉算法两个重要内容，交叉概率PC和变异概率Pm的选择对算法的过程和效果以及收敛性有重要影响。Srinvivas等[13]提出一种能按照适应度值调整Pc和Pm的自适应遗传算法，这两个参数调节公式如式(6)、式(7)。

(6)

(7)

其中，fmax、fav以及f'分别代表种群中的最大适应度值、平均适应度值和进行交叉操作的较大的适应度值。

另外，任子武等[14]提出一种采用了精英保留策略的改进自适应遗传算法，其调节公式如式(8)、(9)，

(8)

(9)

式中，Pc1=0.9，Pc2=0.6，Pm1=0.1，Pm2=0.01。

两种自适应遗传算法能够自适应调整，确保优良个体不被遗传操作破坏，但在适应度、过程停滞等方面还存在不足。本文基于这两种算法，改进自适应遗传算法的Pc、Pm，使其能根据适应度对这两个控制参数实现动态调整，其中，Pc、Pm的自适应调整的公式如(10)、(11)，

(10)

(11)

式中，fmin、f代表群体中的最小适应度值及要变异体的适应度值，Pc1>Pc2>Pc3，Pm1>Pm2>Pm3，它们的取值都在(0,1)区间内，并且在寻优过程内不断进行调节。

改进的自适应遗传算法会依据群体fmax、fmin、fav来判断群体中个体自适应度值的分散程度，同时，本文采用的改进交叉概率Pc、变异概率Pm以种群为单位，依据种群个体的适应度值在种群最大、最小以及平均适应度值的范围内自适应地进行调整变化。改进后的Pc和Pm可以满足自适应调整，在群体最大适应度值中不会为零，相当于增大了群体中优秀个体的交叉概率和变异概率，防止这些个体演化出现停滞不前的情况。同时，将个体的适应度与当代种群的平均适应度进行比较，在进化过程中使种群的优良个体得到保留，种群较差个体的变异能力得到增强，从而使算法跳出局部最优解，增强了算法的全局搜索能力，预防早熟收敛现象，使遗传算法的收敛性、鲁棒性及优良解的多样性得到保障和提高，实用性强。

3.2 基于改进算法的自抗扰控制器设计

本文改进自适应遗传算法进行ADRC参数寻优，并对其优化过程的具体步骤进行设计，使复杂的参数整定简单、精确、可靠。其参数优化过程如图4所示。

图4 改进算法的自抗扰控制器参数优化过程图Fig.4 Parameter optimization process diagram of ADRC of the improved algorithm

优化过程的具体步骤如下：

(1)确定适应度函数。本文将式(12)作为目标函数指标，用来评价系统动态性能、改善控制能量、控制输入受限的性能评价，满足控制优化设计要求。

，

(12)

其中，e(t)为系统误差，y(t)为系统的控制输出，σ(t)为系统的超调量。ω1，ω2，ω3为权重系数。适应度函数f=1/(J+ε)，ε是一个很小的实数。

(2)参数编码。对二阶自抗扰控制器中需要调节的参数向量t的参数进行实数编码。

(3)产生初始种群。为了易于收敛，尽可能选取较大的群体规模值，本文选取群体规模N=20，为了使参数符合运动趋势，在参数寻优时遗传搜索的空间缩小，操作时间变小。

(4)计算种群适应度。根据所确定的适应度函数，计算每个个体的适应度值，对个体进行评价。

(5)个体选择。对种群个体采用轮盘赌的方式进行选择，选出的优良个体作为新一代的父代个体。

(6)交叉。依照式(10)设定的交叉概率Pc，采用单点交叉的方式将交叉算子用于种群，产生新的个体。

(7)变异。依照式(11)设定的变异概率Pm，以基本变异方式对交叉配对后的个体进行基因变异操作，得到新个体。

(8)终止判断。重新评估新一代种群中染色体性能，重复(4)～(8)步操作。设置终止迭代数G=200，当满足迭代终止条件时停止操作。结果表明，此迭代数满足效果要求，再增加计算量和时间，改善效果变化不大。

将改进后的自适应遗传算法与基本遗传算法进行对比，分别对自抗扰控制器进行参数整定，仿真条件、环境参数取值与之前自适应算法仿真保持一致。在经过50代进化后，在参数寻优过程中遗传算法与改进自适应遗传算法的自适应值变化分别如图5所示。

图5 改进算法前后自适应度值变化曲线Fig.5 Fitness value changing curve before and after algorithm improvement

由图5可以看出，使用改进后的自适应遗传算法与之前算法相比，最终得到的种群适应度值更大，说明种群的优良性得到提高，由改进后的算法获得的参数向量能使控制器有更好的控制性能。同时，改进算法还改善了收敛速度过快的问题。比较两条变化曲线可知，改进的自适应遗传算法的参数寻优效果比基本遗传算法好。

4 仿真

将系统中存在的不确定扰动考虑在内，将超空泡速航行体的所处深度由开始的0 m调整到3 m的过程中系统状态变化量z、θ、q、ω的变化情况如图6所示，系统控制输入δc、δf的变化曲线如图7所示。

图7 改进自抗扰控制的系统控制输入Fig.7 System control input of improved ADRC

图6、图7中的虚线和实线分别为自抗扰控制器及其改进后各状态变量的变化曲线，从图中可以看出在系统初始状态偏离了平衡状态，由于自抗扰控制器的加入，航行体的深度重新达到预设位置并且能够维持稳定，超调量很小，纵向速度、俯仰角和俯仰角速度也基本上都在这一时间到达并保持在稳定状态。

另外，由图6、图7可以看出,自抗扰控制器经过优化后，各状态变量恢复到平衡位置的调节时间缩短。位移没有超调量的产生，纵向速度、俯仰角与俯仰角速度从初始状态至期望状态的波动幅度减小，而控制面存在的振荡也得到了有效抑制。由此可知，与参数未经优化的应用于超空泡航行体控制系统的人自抗扰控制器相比，优化后的自抗扰控制器系统的鲁棒性和抗扰动能力更强，参数适应能力更好，其控制性能获得提高。

5 结论

本文根据超空泡航行体的运行特点设计了自抗扰控制器，并提供了一种新思路，即针对自抗扰控制器存在的缺点提出改进的自适应遗传算法并对其参数进行优化。同时，利用MATLAB中搭建了超空泡航行体和自抗扰控制的仿真平台，分析了超空泡航行体在开环状态下各状态变量的动态性能，验证了自抗扰控制器对超空泡航行体优化控制的可行性。

[1]熊天红,易文俊,吴军基,等.水下高速航行体超空泡减阻特性数值模拟研究[J].船舶工程,2008,30(6):11-14.

[2]白涛,毕晓君.水下超空泡航行体纵向机动运动控制研究[J].哈尔滨工程大学学报,2011,32(4):445-450.

[3]张乐,张国鑫.超空泡航行体绝对稳定控制设计[J].装备制造技术,2015(2):5-8.

[4]孙尧,赵新华,莫宏伟.水下超高速航行体的动力学建模及控制问题研究[J].哈尔滨工程大学学报,2008,29(2):144-150.

[5]KIRSCHNER I N, UHLMAN J S,PERKINS J B. Overview of highspeed supercavitating vehicle control[C]// AIAA Guidance, Navigation, and Control Conference and Exhibit. Keystone, Colorado: American Institute of Aeronautics and Astronautics Inc, 2006: 3100-3116.

[6]韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008:3-9.

[7]董莉莉. 自抗扰控制技术在微机电换能器中的应用 [J]. 控制理论与应用, 2013, 30(12): 1543-1552.

[8]高志强.自抗扰控制思想探究[J].控制理论与应用,2013，30(12),1498-1510.

[9]王茂励.超空泡航行体的数学建模与控制方法研究[D].哈尔滨:哈尔滨工程大学,2008.

[10]吕瑞,魏英杰,于开平,等.超空泡航行体的增益自适应全程滑模控制器设计[J].振动与冲击,2011,30(3):34-37.

[11]朱必刚,纪志成.基于永磁同步风力发电系统的自抗扰控制[J].江南大学学报(自然科学版),2011,10(4):385-390.

[12]王东振,文新委,宋刚.自抗扰控制器参数整定的一种新方法[J].黑龙江电力,2012,34(1):71-73.

[13]SRINIVASM, PATNAILK L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Transaction on System, Man and Cybernetics,1994,24(4):656-667.

[14]任子武,伞冶.自适应遗传算法的改进及在系统辨识中应用研究[J].系统仿真学报,2006,18(1):41-43.

Improved genetic algorithm based optimization design of active disturbance rejection controller

TANG Yong-wei1,2, ZHAO Jing-bo1*, WANG Mao-li2,HAO Hui-juan2, LÜ Xiao-hui3

(1. School of Automation Engineering, Qingdao University of Technology, Qingdao 266520, China；2. Shandong Computer Science Center (National Supercomputer Center in Jinan), Jinan 250014, China;3. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China)

∶We present an improved genetic algorithm that can adaptively adjust control parameters based on fitness degree for the force characteristics of supercavitation navigation body and such complicated issues as nonlinearity, time lag and coupling. We construct longitudinal model of supercavitation navigation body, which is controlled by a specific active disturbance rejection controller (ADRC). We further improve adaptive genetic algorithm to precisely optimize it for such issues as mass controller parameters and difficult adjustment. We eventually verify the advantage of the improved ADRC over classical ADRC through simulation. Simulation results show that the improved ADRC satisfies practical requirements and has better control effect.

∶supercavitation navigation body; active disturbance rejection controller; improved adaptive genetic algorithm; decoupling; parameter optimization

10.3976/j.issn.1002-4026.2016.05.001

2016-05-12

国家自然科学基金项目(51475251)；山东省自然科学基金(ZR2013FM014；ZR2015FQ015；ZR2014EEM024)； 山东省自主创新及成果转化专项(2014CGZH0806)

唐勇伟(1991—)，男，硕士，研究方向为控制理论与智能控制。

*通信作者。Email：zhaojingbobg@163.com

TP29

A