改进遗传算法优化设计模糊控制系统的研究

李志刚 宣树人

(华北理工大学电气工程学院研究院，河北 唐山 063009)

改进遗传算法优化设计模糊控制系统的研究

李志刚 宣树人

(华北理工大学电气工程学院研究院，河北 唐山 063009)

对T-S模糊控制器的自动设计进行了研究，提出了一种基于遗传算法的自动设计方法。运用并行分布补偿(PDC)思想将T-S模糊控制器分解为多个局部线性控制器，运用极点配置法设计各个局部线性控制器，所配置的极点参数由改进遗传算法进行鲁棒优化。以单极倒立摆为控制对象，运用所提出的方法进行了T-S模糊控制器的设计，实现了对单极倒立摆的模糊控制。仿真结果表明，该方法实现了T-S模糊控制的自动设计，在T-S模糊控制系统的训练精度、鲁棒性等方面具有更好的效果。

T-S模糊控制器 极点配置 遗传算法 并行分配补偿(PDC) 单极倒立摆 智能控制

0 引言

模糊控制具有较成熟的理论基础和大量的工程应用背景。与传统控制技术及现代控制理论相比，模糊控制系统无需建立在精确的数学模型上，具有方便利用人脑识别、鲁棒性强、抗干扰能力强等特点，这使得其在控制具有复杂性、不确定性、信息量少及高标准性能要求等特点的实际被控对象时具有一定的优势[1]。目前，对模糊控制器设计及方法的稳定性分析虽然已有了大量的研究成果，但在其应用设计中仍然存在控制器的设计、稳定性、鲁棒性等问题。这些问题从一定程度上制约着模糊控制器在实际控制中的应用。

1 单极倒立摆系统建模

单级倒立摆是控制理论有效性验证的经典对象，单级倒立摆的模糊控制是智能控制的一个重要分支[2-4]。本文以单级倒立摆为控制对象，研究了改进遗传算法在T-S模糊控制参数优化中的应用效果。单级倒立摆结构如图1所示。

图1 单极倒立摆结构图

Fig.1 Structural drawing of single inverted pendulum

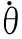
通过对单级倒立摆的小车和摆杆进行受力和运动学分析，可得单级倒立摆的状态方程和输出方程为[5]：

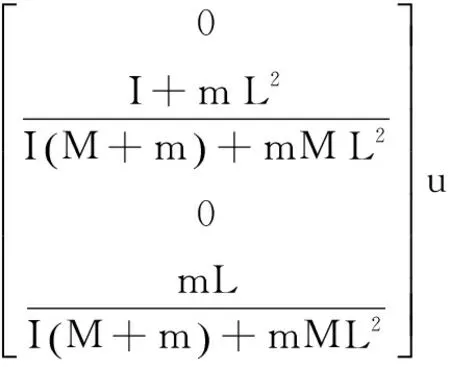
(1)

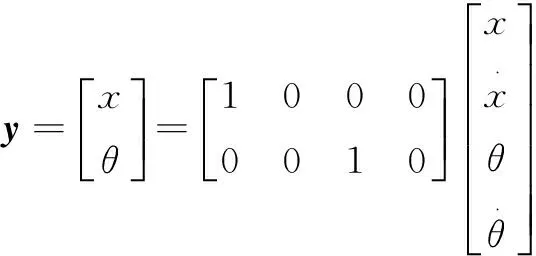
(2)

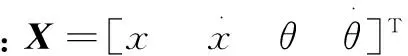
(3)

对于线性定常连续系统，可判断系统完全可控的秩判据为：

rank(B AB…An-1B)=n

(4)

式中：A、B分别为控制系统的状态方程的状态变量矩阵和控制输出量的系数矩阵，即为系数矩阵A的维数。

将式(3)中的状态变量矩阵X和控制输出量的系数矩阵及状态变量矩阵X的系数矩阵的维数分别代入式(4)中的A、B和n中，可知式(4)成立，即建立的单级倒立摆模型完全可控。

2 T-S模糊控制器的设计

模糊控制系统主要由模糊控制器、被控对象和反馈传统通道等组成。其中，模糊控制器是模糊控制系统的核心，故模糊控制器的设计是模糊控制系统设计的关键。在模糊控制中，T-S模糊控制器最具有代表性[6]。本文以并行分布补偿法(parallel distributed compensation,PDC)为基本思想，结合控制理论中的极点配置法，实现了T-S模糊控制器的设计。

PDC思想是将整个非线性T-S模糊控制系统分为各个局部线性控制器，并利用现代控制理论中的控制方法对各个局部线性控制器进行设计，最后应用T-S模糊运算将各个局部线性控制器的输出“聚合”[7]。PDC可分为直接法和试凑法两种。其中，直接法通过分析T-S模糊控制系统的稳定性条件，将T-S模糊控制器的设计转化为一个线性矩阵不等式的求解问题[8-10]；试凑法在设计各个局部线性控制器时只考虑设计而不考虑各部分的相互联系，难以真正实现T-S模糊控制系统的自动设计[11]。本文在对T-S模糊控制器进行了大量研究的基础上，提出了结合极点配置和试凑法设计T-S模糊控制器的思路，并采用改进的遗传算法对配置的极点进行优化约束，从而给出了解决T-S模糊控制器设计的自动设计问题及设计过程中收敛性问题的方法。

根据单级倒立摆控制模型的特点，本文设计了一款集成4个输入和1个输出量的模糊控制器。4个输入量分别为模糊单级倒立摆的位移、速度、角位移和角速度，输出量为控制量u。4个输入量的模糊语言变量都为3个，分别为NL、ZR、PL，即其有81个规则。T-S模糊控制系统可以被认为是多个局部线性系统利用模糊规则的“聚合”，可运用并行分布补偿法思想和极点配置法，将各个局部线性控制器的反馈控制极点设置为所需要的反馈控制极点。因此，确定各个局部线性控制器的极点是设计T-S模糊控制系统的关键。并行分布补偿法中的试凑法无法控制设计时间，也无法实现自动设计；直接法将设计问题转化为标准线性矩阵不等式(linear matrix inequality,LMI)问题时，需要人为给定部分参数，同样无法实现自动设计[11]。为了实现T-S模糊控制器的自动设计、保证控制时间，本文采用了基于改进遗传算法的试凑法进行T-S模糊控制器设计。具体设计步骤如下。

①确定T-S模糊控制器的输入量、输出量及相应的语言变量个数、隶属度等基本参量。

②遗传算法运行所需初始种群的每个染色体由各个局部线性控制器的极点组成，其中的各个局部线性控制器是运用极点配置法求得的。

③应用改进遗传算法，对各个局部线性控制器的极点参数进行优化，求得最优T-S模糊控制器。

3 改进遗传算法

3.1 适应度函数

根据单极倒立摆控制器的特点，本文以单极倒立摆的的输出位移误差、输出角位移误差及模糊控制器的输出控制量作为参考指标，以保证单极倒立摆达到稳态时间所需的时间较少以及单极倒立摆在控制过程中的振荡较小。适应度函数为：

(5)

3.2 初始种群的产生

在解决实际问题时，问题的求解往往伴有约束条件，初始种群的优劣对遗传算法的性能有较大的影响[12-14]。为了保证初始种群中的染色体为有效染色体，改进遗传算法的初始种群中的染色体不再随机产生。随机设置单级倒立摆的初始状态，优化其反馈控制极点参数，并将T-S模糊控制器中的各个局部控制器的反馈控制极点设置为优化得到的反馈控制器的反馈控制极点。每个染色体的81组数依次排列，代表81组局部控制器的反馈控制极点参数，其均为优化得到的反馈控制器的反馈控制极点参数，既保证了各染色体的收敛性，又保证了初始种群的多样性。同时，与以Lyapunov稳定性判据作为约束条件产生的初始种群相比，本文所提出的方法更简易，更适用于T-S模糊控制系统的自动优化。初始种群的产生分为以下两个步骤。

①优化倒立摆反馈控制极点。优化倒立摆反馈控制极点的遗传算法与改进的遗传算法所产生的初始种群不同，而其他的遗传算子及适应度函数则相同。优化倒立摆反馈控制极点只优化1个反馈控制器。根据单级倒立摆的初始状态等优化4个极点，初始种群中的每个染色体均由在设置范围内随机产生的4个参数所组成，分别代表1个反馈控制器的配置极点的共轭极点的实部、阻尼系数和其他2个极点与共轭极点的实部绝对值的比值。随机产生100个初始状态，并运用上述遗传算法得到优化结果。

②由上文可知，T-S模糊控制器需要优化81个局部反馈控制器，共有326个极点。本文采用二进制编码方法，产生含有100个染色体的初始种群。初始种群中的每个个体分别对应第一步中随机设置的100个初始状态。每个染色体依次为81组数据，且81组数据相同，都为所对应初始状态的优化倒立摆反馈控制极点的4个优化参数。

3.3 改进遗传算法

与基本遗传算法相比，本文遗传算法的改进主要体现在两个方面。一是初始种群不再随机产生；二是进行遗传操作时，采用了保留最佳个体策略。虽然在交叉变异的过程中，产生的新染色体可能不具有收敛性，但其适应度会无限趋近于零，故无需单独处理。

改进遗传算法分为两部分，首先利用遗传算法设置遗传算法的初始种群；初始种群生成后，再利用遗传算法优化T-S模糊控制器的各局部线性控制器的极点。改进遗传算法流程图如图2所示。

图2 改进遗传算法流程图

Fig.2 Flowchart of improved genetic algorithm

4 试验仿真分析

本文首先运用提出的T-S模糊控制器的设计方法，对单级倒立摆进行建模，然后从控制器的控制精度和鲁棒性两方面分析该设计方法的有效性。随意选取两组初始状态X1=[0.1 0 0.2 0]T和X2=[0.2 0.1 0.1 0]T。由上文中所建立的单级倒立摆模型及可控性判据可知，所建立的单级倒立摆完全可控。以X1为初始状态，运用本文给出的设计方法，优化单级倒立摆的反馈极点控制模型。最后，通过对比本文设计方法与其他设计方法设计过程、设计精度及设计的T-S模糊控制系统的鲁棒性，验证了本文设计方法的优化性。

4.1 改进遗传算法的优化过程及结果对比

改进遗传算法优化的单级倒立摆反馈控制系统模型的优化参数共有4个，即改进遗传算法的每个染色体由4个参数组成。每个染色体中，代表共轭极点的实部参数的取值范围可取为[-10,0]，阻尼系数的取值范围可取为[0.5，0.99]，其他两个极点与共轭极点的实部绝对值的比值可取为[3,7]。改进遗传算法采用二进制编码方法，以上述4个参数的范围为取值范围随机产生染色体。通过改进遗传算法优化，得到优化的4个参数分别为1.144 9、0.691 5、4和4，对应的4个极点分别为-1.144 9 + 1.196 0i、-1.144 9 - 1.196 0i、-4.694 1 + 0.000 0i、-4.579 6 + 0.000 0i。将所得到的参数分别代入单级倒立摆反馈控制系统和T-S模糊控制器中，可得到二者的初始状态为X1单级倒立摆的适应度函数值分别为642.800 8和527.699 6，二者的仿真结果对比图如图3所示。

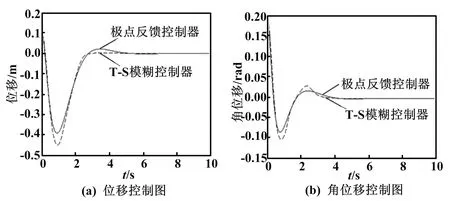
图3 初始状态为X1的单级倒立摆控制仿真结果

Fig.3 Simulink results of single inverted pendulum control in initial condition for X1

同时，为了研究改进遗传算法的优化效果，本文采用了其他2种遗传算法对单极倒立摆T-S模糊控制系统进行优化，分别为设定初始种群产生的遗传算法和保留最佳个体策略遗传算法。其中，初始种群产生遗传算法的初始种群产生方法与改进遗传算法相同。由于随机产生初始种群可能导致保留最佳个体策略基本遗传算法无解，所以三种遗传算法的初始种群都设定了5个相同的特定初始个体，即T-S模糊控制各个控制器的极点分别为控制系统控制器的最佳反馈极点参数。改进遗传算法与其他2种遗传算法的极点参数寻优过程对比如图4所示。

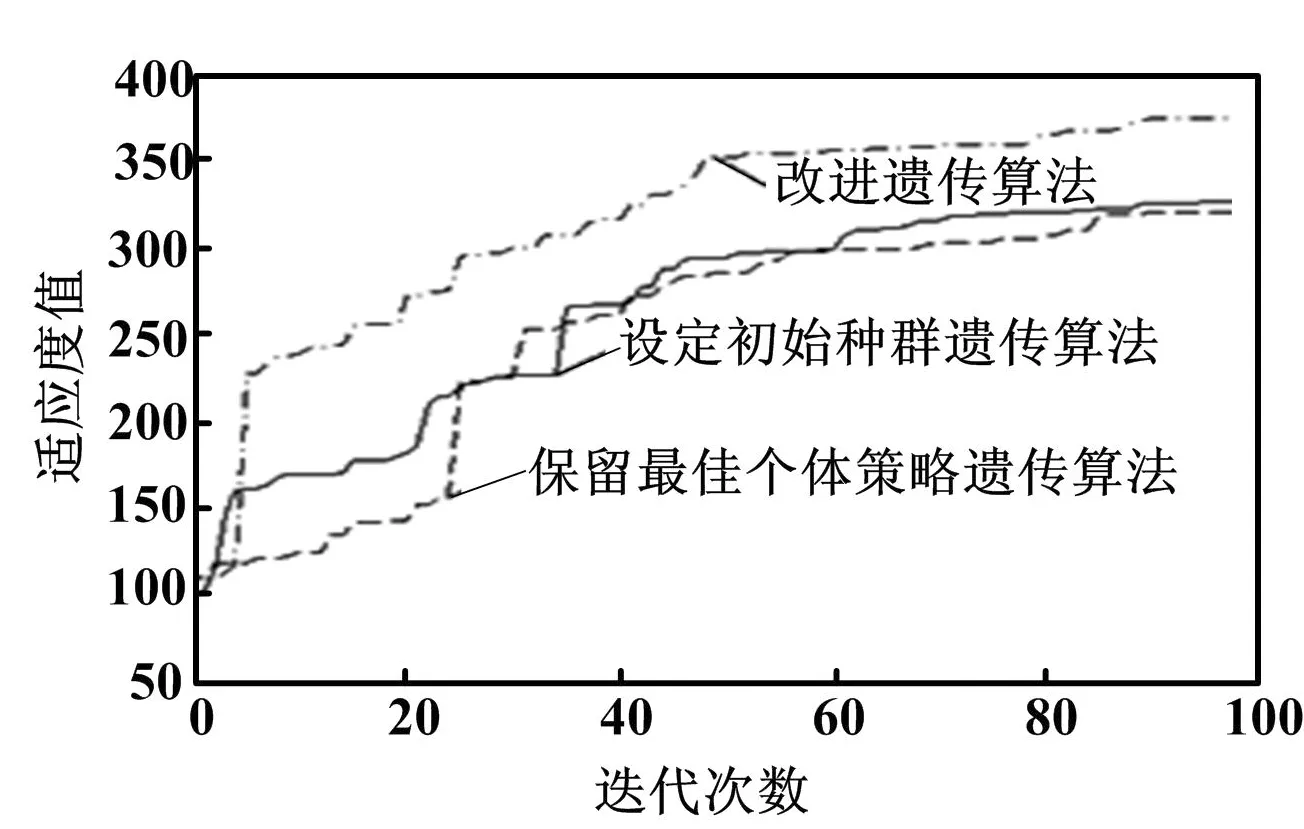
图4 三种遗传算法优化过程对比图

Fig.4 Comparsion diagram of improving process in three genetic algorithm

由图4可以看出，在极点参数的寻优精度和速度上，改进遗传算法都优于其他遗传算法。其主要原因在于，在设定初始种群遗传算法中，遗传算子随机运算所产生的染色体，不能保证群体中的最优个体有效的保存和进化；最佳个体策略有助于保证遗传运算中染色体个体的有效性，但随机产生的初始种群难以保证群体的高效进化。改进遗传算法综合二者的优点，更有利于寻找最优解。

4.2 改进遗传算法的鲁棒性对比

控制系统的控制器参数不变，将两个控制系统中被控对象的初始状态由X1改为X2,单级倒立摆的适应度标函数值分别为105.500 9和75.245 8。二者的仿真结果对比图如图5所示。

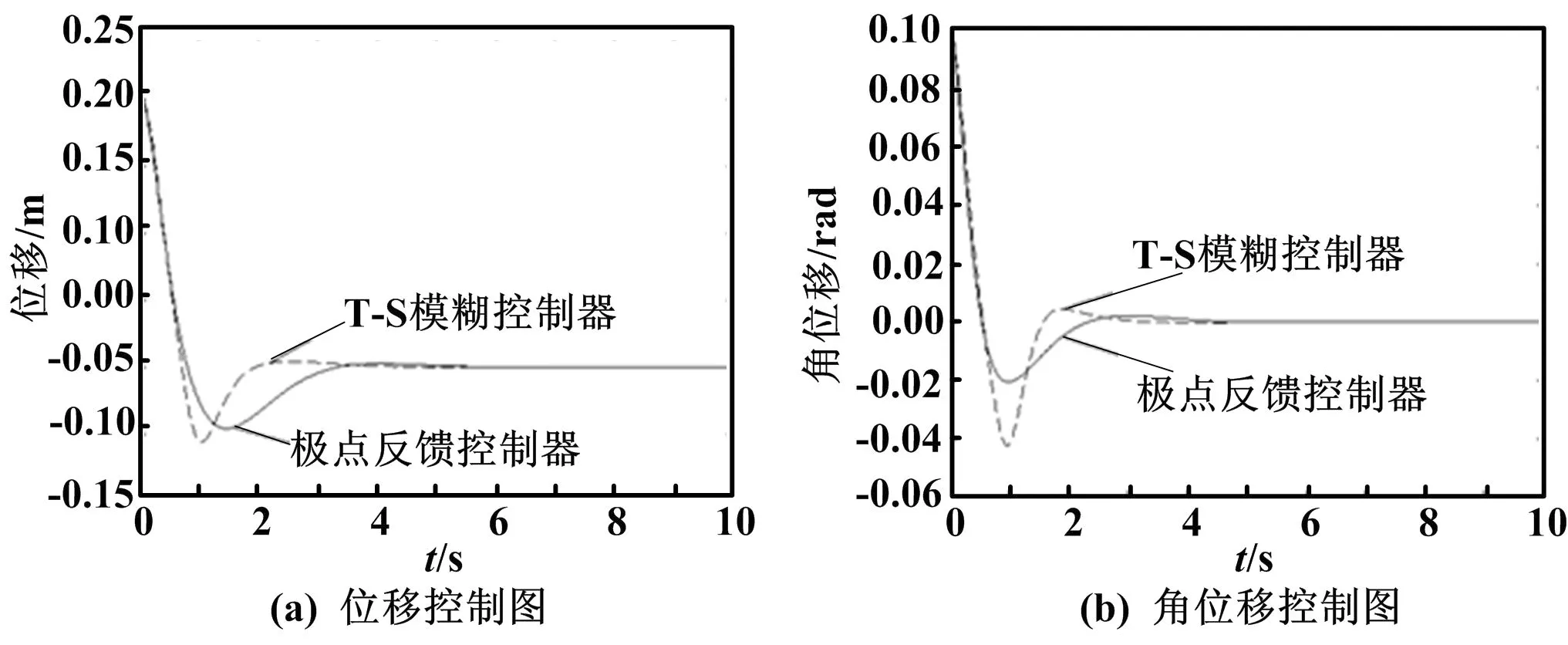
图5 初始状态为X2的单级倒立摆控制仿真结果

Fig.5 Simulink results of single inverted pendulum control in initial condition for X2

由图5可知，本文所提出的改进遗传算法优化的T-S模糊模糊控制器，其控制效果优于普通的倒立摆极点反馈控制。虽然对于初始状态为X1的单级倒立摆，T-S模糊控制器的控制效果略优于反馈极点配置控制，但对于初始状态为X2的单级倒立摆，T-S模糊控制器的控制效果要好得多。同时，为了研究改进遗传算法的鲁棒性，本文进行了100次试验，每次试验随机选取1个被控对象的初始状态，运用设计的T-S模糊控制器和极点反馈控器分别对其进行控制，并记录控制结果的适应度函数。最终试验表明，改进算法设计的T-S模糊控制器的控制效果好于反馈控制系统的控制效果的情况占试验总数的86%，其鲁棒性明显优于反馈系统控制。

5 结束语

本文提出了一种基于PDC和线性控制理论中极点配置方法的T-S模糊控制器的设计方法。为了实现T-S模糊控制器的自动设计，在设计过程中，以改进的遗传算法对设计的T-S模糊控制器进行反馈极点的参数优化。以单级倒立摆为研究对象，采用改进遗传算法对其进行了仿真研究。仿真结果显示，采用该方法所设计的控制系统具有良好的稳定性和鲁棒性。

[1] 张义捷,钟友武,许得军.基于模糊控制技术的飞行器姿态控制系统设计[J].航天控制,2013，31(2):31-35.

[2] 薛占熬,李跃军,程惠茹,等.二级倒立摆的区间值模糊控制[J].计算机工程与设计,2013，34(9):263-267.

[3] 郑海平,钟晨星,呈利平,等.基于增益调试型参数自调整的倒

立摆模糊控制[J].华中科技大学学报(自然科学版),2013，41(5):5-8.

[4] 王琪,黄华.倒立摆系统的符号型自适应模糊控制[J].计算机工程与设计,2014，35(3):284-288.

[5] 胡桂红.基于遗传算法的倒立摆控制策略研究[D].西安：西安电子科技大学,2008.

[6] 石辛民,郝整清.模糊控制及其MATLAB[M].北京：北京交通大学出版社,2008.

[7] 张果,庄淑君.模糊系统时滞相关模糊控制器的设计[J].北京理工大学学报,2013，33(2):151-155.

[8] 王艳阳,李以家,郑玲,等.基于Takagi-Sugeno模型的磁流变半主动悬架控制[J].系统仿真学报,2013,5(5):1065-1068.

[9] 厉虹,邹奎.基于T-S模糊模型的3D刚体摆姿态控制[J].控制与决策,2013，28(12):29-35.

[10]王铁超,佟绍成.一类不确定非线性系统的执行器故障模糊容错控制[J].模糊系统与数学,2011，25(2):97-109.

[11]陈国洋.一类T-S模糊控制系统的稳定性分析及设计[D].上海：上海交通大学,2009.

[12]范小勤,汪小红.约束优化问题的一种改进遗传算法的收敛性分析[J].自动化与应用,2015,34(9):6-10.

[13]汪春峰,张永红.基于无约束优化和遗传算法的贝叶斯网络结构学习方法[J].控制与决策,2013(4):618-622.

[14]金弟,刘杰,杨博,等.局部搜索与遗传算法结合的大规模复杂网络社区探测[J].自动化学报,2011，37(7):873-882.

Improved Genetic Algorithm for the Research of Fuzzy Control System Design

To study the automated design of T-S fuzzy controller,a design method of T-S fuzzy controller based on improved genetic algorithm has been developed.Using parallel distributed compensation (PDC) theory,the T-S fuzzy controller is decomposed into several local linear controllers,and each local linear controller is designed by pole assignment method.The pole parameters are configured for robust optimization by improved genetic algorithm.At last,this paper takes the single inverted pendulum as control object and operated it according to T-S fuzzy controller designso as to verify the validity of the design method of T-S fuzzy control system proposed.The simulation results indicate that the improved method makes the automatic design of T-S fuzzy controller possible,and has a better performance in training precision androbust optimization in terms of the T-S fuzzy control system.

T-S fuzzy controller Pole-placement method Genetic algorithm Parallel distributed compensation(PDC) Single inverted pendulum Intelligent control

河北省自然科学基金资助项目(编号：F2013209203)。

李志刚(1966—)，男，2011年北京交通大学博士后流动站开展博士后出站，教授；主要从事数据挖掘在智能控制领域的应用研究。

TH165;TP18

A

10.16086/j.cnki.issn 1000-0380.201612002

修改稿收到日期：2016-06-09。