基于ANSYS的糊底机机架模态分析
张 伟
(兰州交通大学机电工程学院,甘肃 兰州 730070)
基于ANSYS的糊底机机架模态分析
张 伟
(兰州交通大学机电工程学院,甘肃 兰州 730070)
纸纱复合袋糊底机的机架是整机的主要承载结构,其强度和可靠性对整机安全高效生产至关重要。针对机架的工作特性,利用有限元分析软件ANSYS对机架的工况性能进行研究,保证其具有富裕的强度和良好的动态特性。在SolidWorks中建立机架模型并简化,在ANSYS中进行静态及模态分析。通过分析得到糊底机机架在工作时的应力大小、应变位置及该机架的前十阶固有频率、振型及总振幅。分析结果可为后续的样机设计、机架结构优化设计和改进提供参考和理论依据。
纸纱复合袋糊底机 机架 ANSYS 模态分析 静态分析 有限元分析 应力分布 振动特性
0 引言
近年来研制的纸纱复合袋糊底机较好地解决了纸纱袋的生产效率问题,但大量工作流程仍需由人工完成,成本高、自动化程度低等问题仍普遍存在[1]。国外虽已有自动化纸纱复合袋糊底机,但跨国引进存在耗费资金量大、售后困难、产品规格不一致等限制因素,因而设计研发符合我国产业需求的纸纱复合袋自动化糊底机迫在眉睫[2]。自动化糊底机包括若干复杂机构,如压痕机构、切口机构、吸开机构、涂胶机构等,这些重要机构都需由机架支撑、固定、配合、容纳,以协助完成糊底工作。工作时,机架要承载来自自身的振动和若干复杂机构的巨大自重载荷。为确保机架有足够的强度并符合机架振动特性,本文基于模态分析基础理论,通过有限元分析软件ANSYS对工况下的糊底机机架进行分析,得到机架应力分布状况和动态特性,并验证了机架强度,从而缩短设计周期、保证机架设计合理。
1 模态分析理论
模态分析可以用来确定结构部件的模态参数,即结构的固有频率和振型[3]。通过模态试验获得结构模态参数的方法存在过程繁琐、耗时较长、试验成本高等问题,在机械产品的设计初期和研发阶段并不经济实用。而有限元分析方法通过构建合适的结构模型,较为准确地计算出结构的模态参数和响应特性,为产品的初期设计研发提供了可靠、有效的模态特性预测平台,故采用有限元模态分析方法来初步掌握机架结构的模态参数[4-5]。
假设糊底机机架是一个有n个自由度的物理模型,根据达朗贝尔原理和胡克定律,通过对作用在系统上的外力中加入惯性力,即可建立物理坐标系统中n自由度的糊底机机架系统方程。机架的振动方程为:
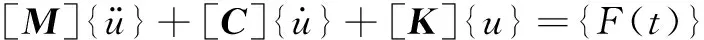
(1)
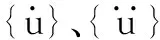
理论分析与实践均表明,机械结构的固有频率由结构自身的属性所决定,不受外部载荷影响,同时阻尼对结构的固有频率和振型也影响不大[6]。因此,对于无阻尼自由振动结构,其动力学方程式中的阻尼项和外加激励项均为零,式(1)可以简化为:
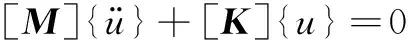
(2)
任何弹性体的自由振动总可以由一系列简谐振动组合而成[7],因此可以设上述方程的解为:
{u}={δ}eiωt
(3)
式中:ω为固有频率;{δ}为系统振幅列阵向量,即振型向量。将式(3)代入式(2),有:
([K]-ω2[M]){δ}=0
(4)
式中:ω2为系统特征值;{δ}为系统的特征向量。
式(4)被称为系统的特征矩阵方程。其中,系统的固有频率和固有振型的求解问题是通过求解式(4)中的ω2和{δ}来确定的。
由于系统在自由振动时,振幅向量不可能全都为零。因此,由线性代数理论可知,要使系统的特征矩阵方程式(4)有解,就必须保证式(4)中系统的特征向量{δ}的系数行列式等于零[8],即:
|[K]-ω2[M]|=0
(5)
当结构的质量矩阵[M]和刚度矩阵[K]均为n阶方阵时,式(5)被称为ω2的n次实系数方程。由式(5)可以确定系统的n阶固有频率,进而由式(4)确定系统的振幅向量{δ}。
2 机架模型的建立
2.1 机架实体模型的建立
根据设计图纸和总体布置方案,本文首先运用SolidWorks软件平台建立机架各个组成部分的零件图,然后装配生成糊底机机架的三维实体模型,如图1所示。糊底机整机的机架总长为5 880 mm,宽为1 140 mm,高为1 000 mm。机架的零件均采用40 mm×40 mm的口字型方钢,壁厚为2 mm。
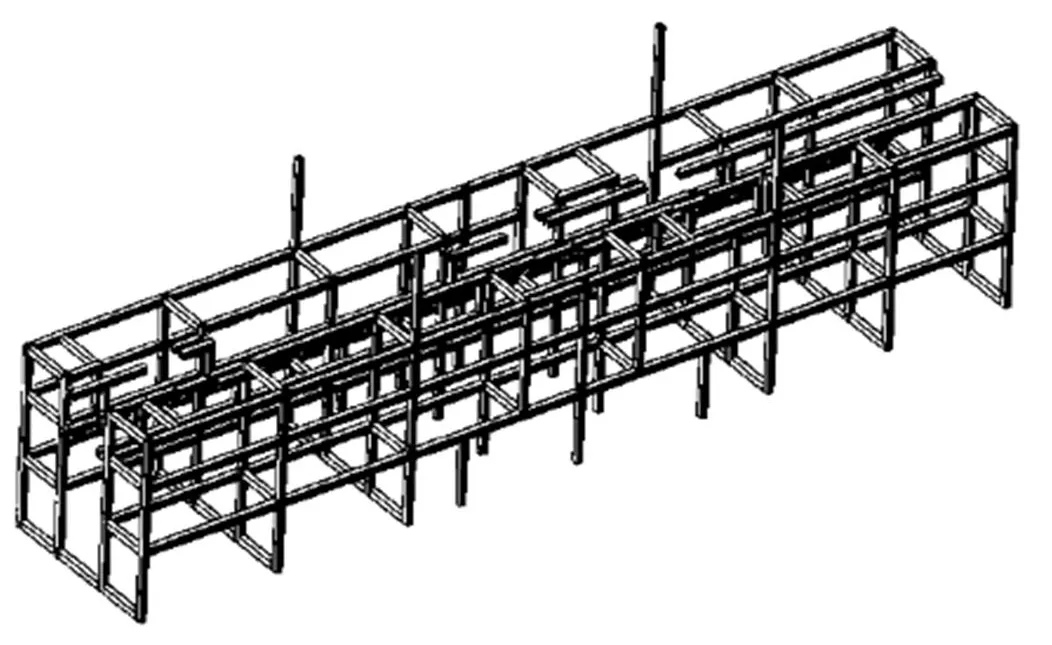
图1 糊底机机架模型
Fig.1 Model of the rack of bottom gluing machine
2.2 有限元网格模型的建立
因整个糊底机机架的布局复杂,为了确保建模机架动力学分析结果与实际结构一致、缩短计算时间,在建立机架有限元模型时,应根据机架实际情况作出如下简化。
①省略对整机机身强度、刚度无影响的部件;
②对一些不重要的装配孔进行简化;
③不考虑铆钉螺钉的预应力;
④忽略焊缝处因材料特性的不同、焊接质量不可靠以及由于焊接而对零件之间作用力而产生的影响;
⑤ 认为大地和机架的连接刚度无限大,对机架与大地连接面进行六自由度全约束。
根据简化要求,在SolidWorks中简化修改模型,将三维实体模型保存成.x-t的格式,并通过SolidWorks和ANSYS的良好接口,在ANSYS 15.0中通过“Import-GreOparametric”导入机架的实体模型。设置单元类型采用8节点六面体三维实体单元solid45,每个节点有3个移动自由度,为使网格划分后的模型既达到精度要求又提高计算效率,指定单元边长为20 mm。网格划分后糊底机机架有限元模型共包括121 275个节点,370 805个单元。
本机架的材料均采用Q235口字型方钢,其弹性模量为206 e+11 Pa,泊松比为0.3,密度为785 0 kg/m2,屈服强度为235 MPa,许用应力为117.5 MPa。其中,许用应力[σ]=[σs]/n,σs为材料的屈服极限,n为材料的安全系数,本文取n=2。
3 机架有限元分析
糊底机机架作为整台机器的支撑部件,要承受若干复杂机构(压痕机构、切口机构、吸开机构、涂胶机构等)施加的静载荷。静态分析是结构分析的前提,通过有限元软件模拟糊底机机架在静态载荷作用下机架各个部分的应力大小、应变分布情况,然后针对应力集中、变形较大等不合理部位,对模型进行合理修改,来提高机架的静态刚度、减小形变。同时,对机架进行模态分析,可以得到机架自身固有频率。尽量将自身固有频率与外界激励频率间的耦合降低到最小,这不仅可以提高糊底机机架的结构刚度和可靠性,同时还可以将糊底机机架的结构负荷降到最小,以保证机架在长期服役期间的安全、可靠、稳定工作,从而提高糊底机整体性能[9]。
3.1 静态分析
3.1.1 边界约束及加载
根据糊底机的实际工作状况,机架前后与地面接触的部件通过地脚螺栓与地基相连,对机架两端与地基接触面的6个自由度全部约束。
压痕机构、切口机构、吸开机构、涂胶机构等按照其支撑位置,被分配在机架的相应位置。由于各个机构的实际质量都大于理论测量质量,故加载时的载荷都略大于理论测得的载荷,并在加载时以面载荷方式加入到机架相应部位,各部分的质量如表1所示。
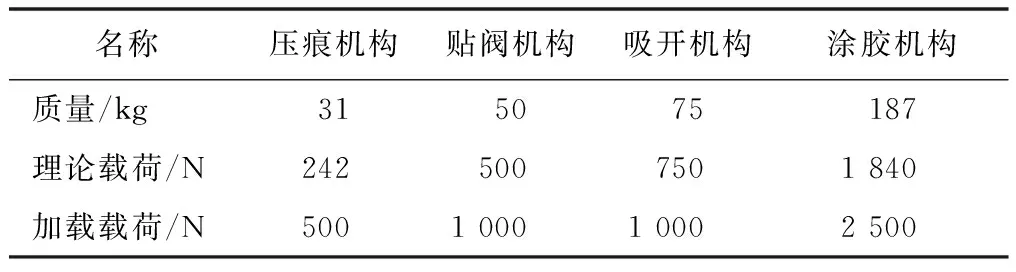
表1 各部分质量Tab.1 Weights of each part
3.1.2 静态结果分析
在所建网格模型的基础上,定义其分析类型为static,进行模型的求解计算。由糊底机机架静力分析结果得出:机架的最大应力值为23.8 MPa,最大变形位移值为2.154 mm。从应力位移分布图可知,机架的最大应力和变形都主要发生在机架中间部位,这与实际机架因中间部位承受质量最大的涂胶机构而发生最大形变的实际情况相符。打开ANSYS应力输出表,找到最大等效应力点为100 906,从中可得节点的主应力为σ1=23.110 MPa,σ2=16.412 MPa,σ3=8.432 MPa。由第三、第四强度理论可得[10]:
σr3=14.678 MPa≤[σ]=117.5 MPa
σr4=12.727 MPa≤[σ]=117.5 MPa
由此可以得出,糊底机机架满足第三、第四强度理论的强度条件,机架在工作过程中有足够的强度,符合工况要求。
3.2 模态分析
根据模态分析理论,机架结构的振动可以表达为各阶固有振型的线性组合,其中低阶振型对机架结构的动力影响程度比高阶振型大,因此低阶振型决定了机架结构的动态特性[11]。根据模态分析的结果,可以得到糊底机机架的相关参数以及机架在不同频率下的振动特性,为机架的设计提供理论依据和参考。在大型有限元分析软件ANSYS中重新定义分析类型为Modal,通过模态分析模块中的兰索斯法[12]对机架进行了模态分析,得到糊底机机架前十阶模态分析结果,如表2所示。
从表2可以看出,机架振动特性的主要表现形式是弯曲及扭转振动。一阶固有频率为13.920 Hz,总振幅为0.087 68 m,振型为机架横向整体弯曲。二阶固有频率为17.508 Hz,总振幅为0.099 97 m,振型为机架纵向整体弯曲。整体机架由两边向中间的弯曲幅度逐渐增大,弯曲容易引起连接处的疲劳损伤,因而需增加中间部位处的刚度。三阶固有频率为19.323 Hz,总振幅为0.117 12 m;四阶固有频率为21.164 Hz,总振幅为0.139 86 m;振型都主要为弯曲。除此之外,三阶、四阶振型伴有不同程度的扭转现象,最大变形位置仍在机架中部,对机架性能的影响与一、二阶振型类似。五阶以上机架开始出现蛇形弯曲及扭转等复杂变形,在机架中部仍旧变形较大,因此机架结构的中部位置是疲劳薄弱位置,在设计时应着重考虑。
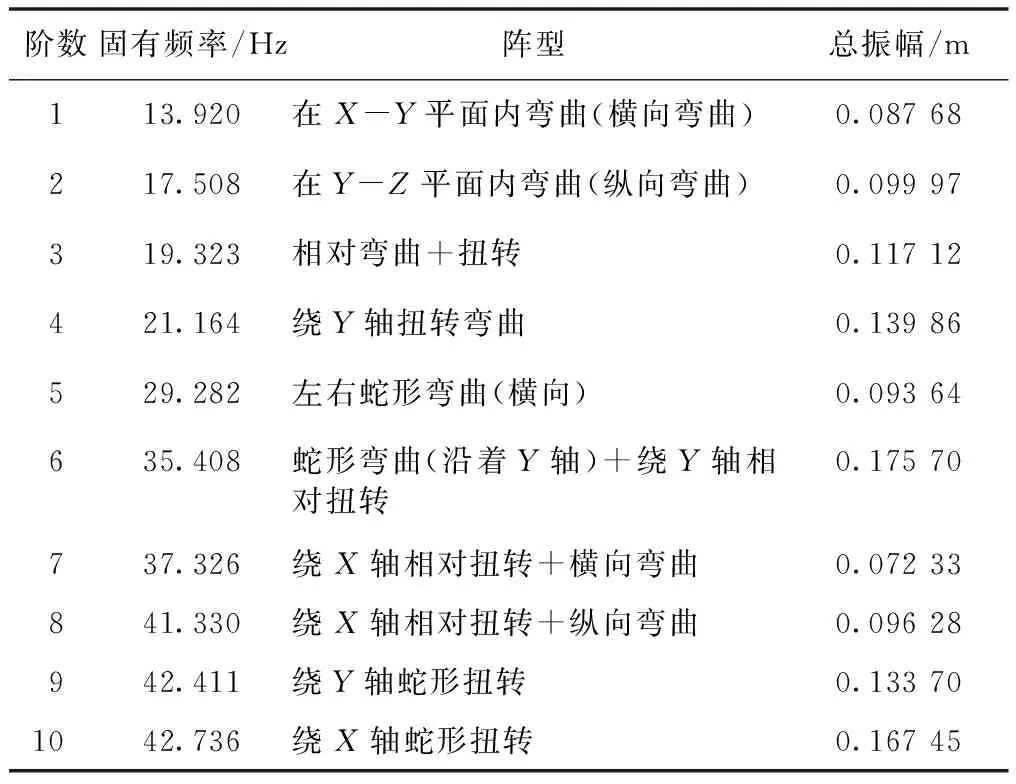
表2 机架的前十阶固有频率、振型和总振幅Tab.2 The first 10-order natural frequency, vibration mode and total amplitude of rack
4 结束语
本文结合糊底机机架的设计要求及相关参数,在SolidWorks中建立机架模型并根据要求简化模型,并通过ANSYS对机架进行了静力和模态分析。由静力分析结果对机架强度进行验证,证明了机架具有足够强度。由模态分析得到机架的固有频率、振型和总振幅,确定了影响该机架振动特性的模态频率主要集中在13.920~42.736 Hz。分析结果为了解机架的振动特性,后续样机的设计投产,机架结构的优化设计和改进提供了理论依据。
[1] 殷红,董海棠,汪诤,等.纸纱复合袋机控制系统设计[J].自动化仪表,2012,33(3):24-27.
[2] 王义兵,彭珍瑞,殷红,等.纸纱复合袋糊底机控制系统设计[J].制造业自动化,2015,37(1):123-126.
[3] 马华永,王卫兵,冯静安,等.基于ANSYS的茬地免耕播种机机架有限元分析[J].农机化研究,2014(4):33-37.
[4] HAMRIT F,NECIB B,DRISS Z.Analysis of mechanical structures using beam finite element method[J].International Journal of Mechanics and Applications,2015,785(1):143-152.
[5] 王轲,范忠华,党西军.基于模态试验与优化的静动力学模型转换[J].振动工程学报,2012,25(1):38-42.
[6] 毛军,董先瑞,谢苗,等.智能立体停车位框架的模态分析[J].工程设计学报,2016,23(1):54-59.
[7] 马丽溟,朱智民,安占飞,等.轿车白车身模态分析[J].振动与冲击,2013,32(21):214-218.
[8] 贺李平,龙凯,肖介平. ANSYS13.0与HyperMesh11.0联合仿真
有限元分析[M].北京:机械工业出版社,2012.
[9] 丛明,房波,周资亮.车—车拉数控机床拖板有限元分析及优化设计[J].中国机械工程,2008,19(2):208-213.
[10]王卫兵,牛健文,晁贯良. 机器鱼壳体三维建模及有限元分析[J].制造业自动化,2011(16):78-80.
[11]熊用华,杜发荣,高峰,等.轻型载货汽车车架动态特性分析与研究[J].机械设计,2007,24(4):60-62.
[12]曾攀.有限元分析及应用[M].北京:清华大学出版社,2004.
ANSYS-based Modal Analysis for the Rack of Bottom Gluing Machine
The rack of the bottom gluing machine for paper-yarn compounded bags is the main load-bearing structure of the machine,its strength and reliability is very essential to safe and efficient production.In accordance with the working characteristics of the rack,under working conditions,the performance of the rack is studied by using ANSYS,to ensure the rack has a wealthy strength and good dynamic characteristics.The model of rack is established and appropriately simplified in SolidWorks,and static analysis and modal analysis are performed in ANSYS.Through analyzing,the stress,strain position,the first 10 order natural frequency,vibration mode and total vibration amplitude of the rack are obtained.Analysis results provide reference and theoretical basis for the subsequent prototype design,structure optimization,and improvement.
Bottom gluing machine of paper-yarn compounded bag Rack ANSYS Modal analysis Static analysis Finite element analysis Stress distribution Vibration characteristics
甘肃省科技支撑计划支持基金资助项目(编号:1504GKCA019) 。
TH122;TP29
A
10.16086/j.cnki.issn 1000-0380.201612006
修改稿收到日期: 2016-05-12。
作者张伟(1991—),女,现为兰州交通大学机械电子工程专业在读硕士研究生;主要从事模态分析方向的研究。

