时域积分的LWD振动加速度处理电路
程晶晶 高 双 范云龙 张嘉伟
(华中科技大学自动化学院1,湖北 武汉 430074;中海油田服务股份有限公司油田技术研究院2,北京 101149)
时域积分的LWD振动加速度处理电路
程晶晶1高 双1范云龙1张嘉伟2
(华中科技大学自动化学院1,湖北 武汉 430074;中海油田服务股份有限公司油田技术研究院2,北京 101149)
根据随钻测井(LWD)仪器的振动位移对随钻测井数据进行评估,是提高随钻测井准确性的有效方法。研制了一种基于时域积分方法的加速度信号处理电路,其可在井下实时测量随钻测井仪器的振动加速度,再通过积分计算获得井下实时振动位移。该电路的数字信号处理器件选用高可靠性的32位定点DSP器件TMS320F2812,加速度信号处理方法选用占用资源少、便于微型系统实时计算的时域积分方法,再采用拟合多项式极值方法,消除了积分中产生的趋势项误差。振动测试表明,该加速度测量电路所得的位移时程曲线与理论值曲线拟合的精度较高,能满足随钻测井仪器位移测量的需求。
随钻测井(LWD) 振动加速度 信号处理 DSP 时域积分 傅里叶变换 趋势项误差
Trend error
0 引言
根据随钻测井(logging while drilling,LWD)仪器的振动位移对随钻测井数据进行评估,是提高随钻测井测量准确性的有效方法[1-2]。测井仪器横向位移对核磁共振信号的影响研究表明,在一个脉冲序列(carr purcell meiboom gill ,CPMG)的脉冲周期内,当钻铤横向位移发生快速变化时,测得的核磁共振信号回波串的幅值明显受到影响,迅速衰减;当在横向位移变化缓慢时,测得的回波串信号影响较小。因此,在随钻核磁测井的数据处理中,需要以CPMG脉冲测量时间内横向及轴向的位移为依据,设计滤波器,以获得可信的信号处理结果[3]。
本文研制了一种加速度信号处理电路,可在井下实时计算随钻测井仪器的振动位移。该电路的数字信号处理器件选用高可靠性的32位定点DSP器件TMS320F2812,加速度信号处理方法选用占用资源少、便于微型系统实时计算的时域积分方法,再采用拟合多项式极值方法,消除了积分中产生的趋势项误差[4]。振动测试表明,对加速度信号积分得到的位移时程曲线平方和误差小于±0.1,能满足随钻测井仪器位移测量的需求。
1 加速度信号处理电路
在随钻测井中,横向振动是石油钻井中钻具组合(钻头、钻柱和钻杆)的主要运动形式之一。横向振动不仅会引起钻具失效,更会对测井工作安全产生较大的威胁;而且其对于非瞬时测量的测井仪器影响较大。比如核磁测井仪器测井时需要极化时间,横向振动会使极化区与共振区的样品测量不一致,从而导致测量的回波信号幅值的衰减。因此,本文根据井下仪器横向振动的特点,设计了基于时域积分的加速度信号处理电路,将采集到的加速度信号在数字信号处理器中进行数值积分,并根据拟合多项式的方法消除了积分位移中的趋势项,得到校正的位移曲线。
1.1 电路整体结构设计
该电路系统由外部2个两轴加速度计传感器、信号转换电路、加速度阈值比较电路以及数据算法处理电路组成。数据算法处理电路采用DSP+FPGA的结构。FPGA选用ACTEL公司的A3P1000芯片,DSP选用TI公司的TMS320F2812芯片。其中,数据处理包括加速度数值积分算法以及拟合多项式消除趋势项算法等,计算的位移值通过RS-485总线上传至主控系统。加速度阈值比较电路是井下钻柱振动特性监测装置的一部分,实时监控井下钻柱动力学特性,是防止钻柱失效的有效手段。加速度采集电路系统框图如图1所示。
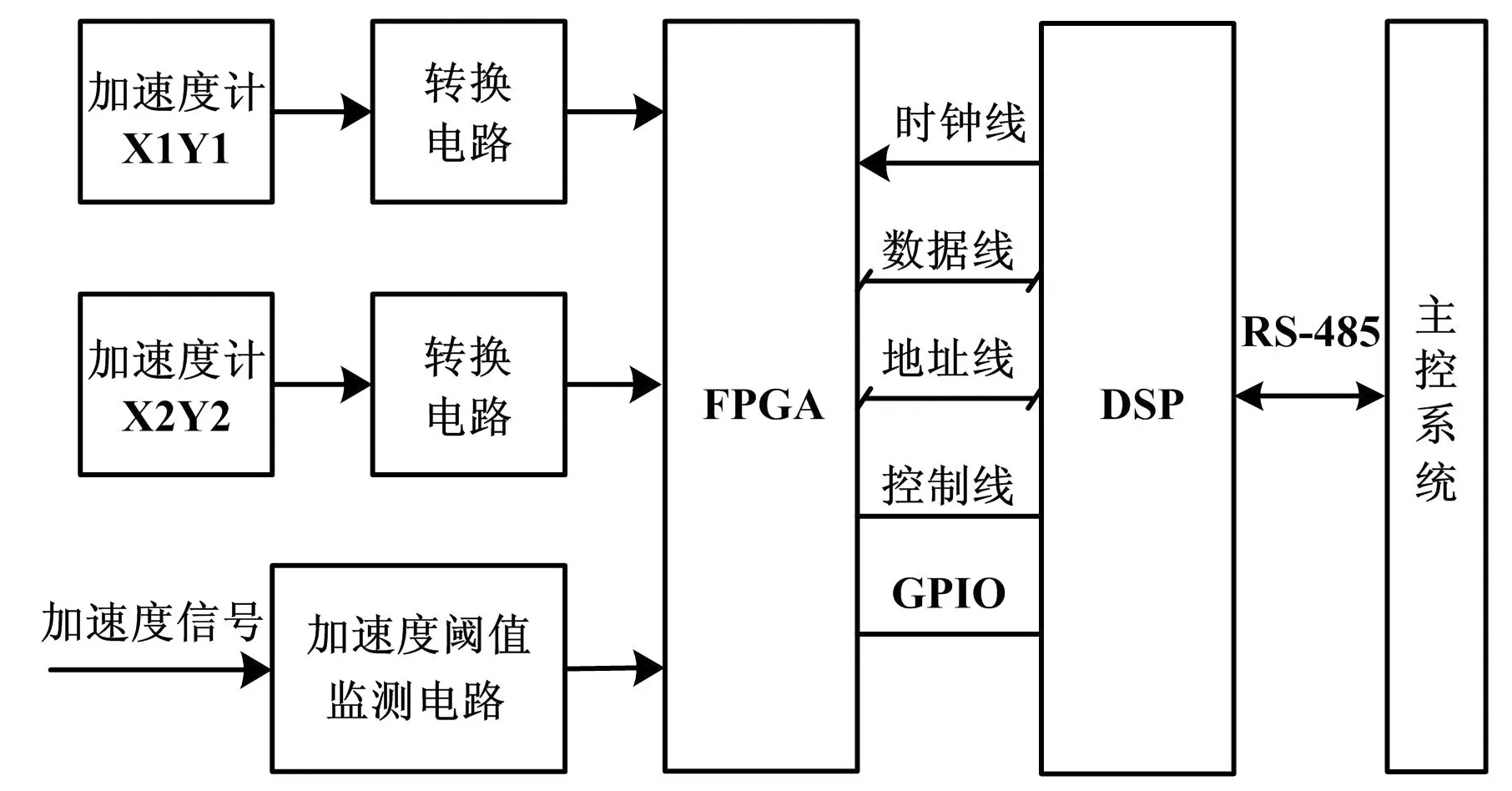
图1 加速度采集电路系统框图
Fig.1 The systematic block diagram of acceleration acquisition circuit
随钻仪器在井下振动的特点为:横向加速度的数值范围广、井下温度高、井下空间狭小以及加速度计安装难。因此,选用的加速度计需要具有灵敏度高、精度高、接口简单、安装方便、耐高温等特点[5]。本设计中选用的集成加速度计是DYTRAN公司的3003B,满足以上测量的特点。加速度计具体参数如表1所示。
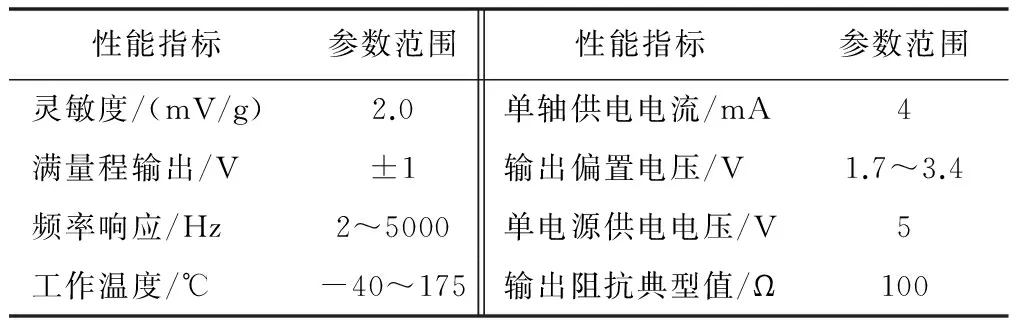
表1 3003B加速度计性能参数表Tab.1 Performance parameters of 3003B accelerometer
信号转换电路由恒流源电路、交流耦合与放大电路、抗混叠低通滤波器以及ADC采集电路等组成。由于井下高温环境对集成运放参数的影响不如对晶体管或场效应管参数的影响显著,所以恒流源电路优先采用带有负反馈的集成运放结构。交流耦合电路CR组成的高通滤波器的截止频率约为2 Hz,可以在将加速度计信号送入后级放大器放大之前,滤除信号中的直流电压。根据ADC的有效分辨率和输入电压的幅值要求,电路增益设计为G=10。抗混叠低通滤波器在-3 dB处的截止频率为2 kHz。设计中,滤波器器件均选用耐高温器件,其中电容选用高温下温度系数较小的NPO电容;电阻选用薄膜型低TCR电阻,其温度可达到175 ℃以上。基准源选用ADI公司的温漂系数低至1 ppm/℃的ADR423,受基准电压源温漂系数的影响,ADC选用的是分辨率为12位、采样率为100 kHz的AD7870。加速度硬件采集电路如图2所示。
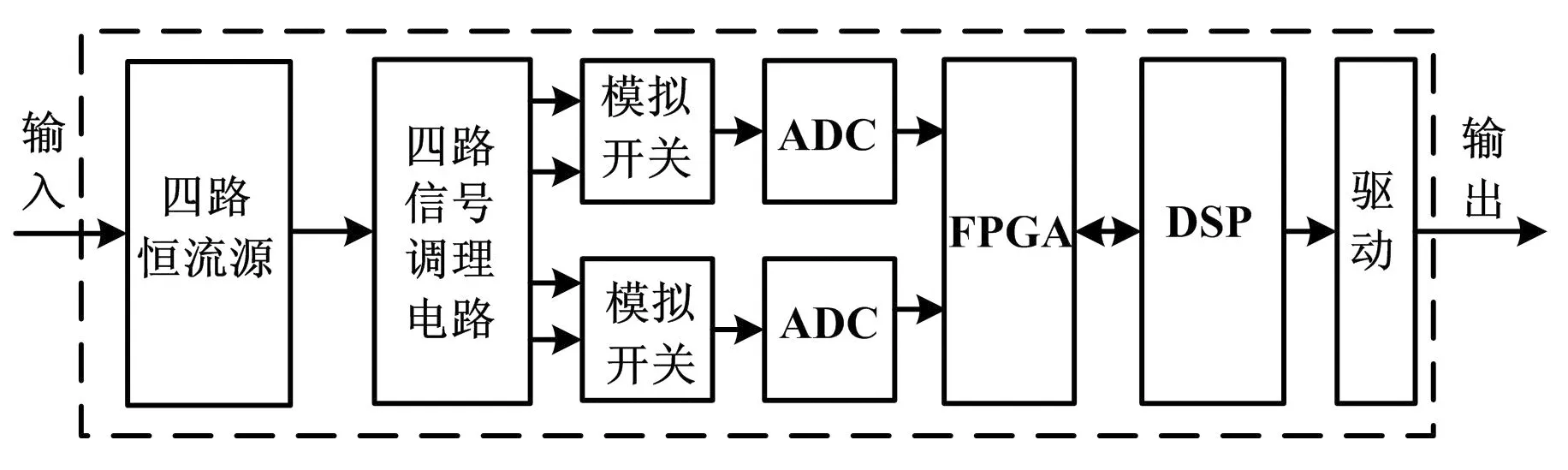
图2 加速度硬件采集电路
Fig.2 The acceleration hardware acquisition circuit
1.2 加速度信号处理算法
根据加速度信号积分得到位移的方法有时域法和频域法。如采用频域的方法,由于傅里叶变换带来的截断误差(如泄漏现象等),会导致位移的计算误差;而频域的方法会占用更多的器件资源和处理时间,给系统的微型化和实时处理带来困难。因此,目前采用得更多的是时域的方法。根据测量的振动加速度信号,由梯形公式的数值积分方法,一次积分可得速度信号,二次积分可得位移信号[6-7]。
根据振动加速度获得速度与位移的值,假定初始加速度与速度均不为零,可以利用的加速度、速度与位移积分的固有关系式如下:
(1)
(2)
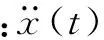
根据梯形积分的关系式,式(1)、式(2)的离散形式为:
(3)
(4)
式中:N为加速度信号的采样点数;Δτ为积分时间的步长,要求积分步长要足够短;Δτ与采样频率fs的关系为Δτ=1/fs。
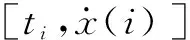
因此,根据最小二乘法拟合趋势项误差,可得如下方程式:
(5)
只要找到一组系数pk,就可以确定E(f)的最小值,并求出拟合多项式的趋势项。因此,根据多元函数求极值的方法,分别对pj求偏导数,可得到如下关系:
(6)
对式(6)变形可得:
(7)
上述等式可以用矩阵表示为:
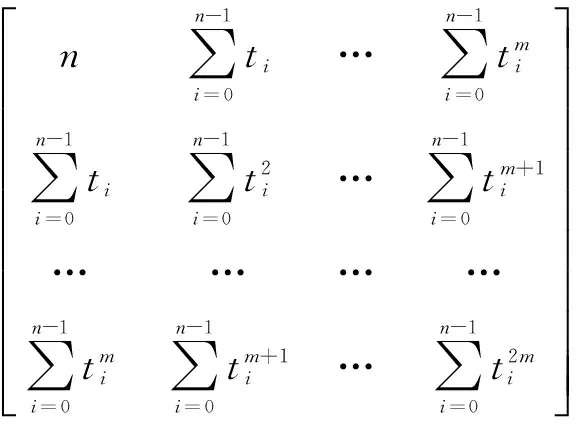
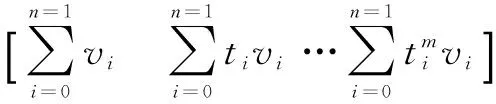
(8)
由于上述方程的系数矩阵为正定矩阵,所以该方程存在唯一解,从而可以求出系数矩阵。因此,求解位移时,取m=2,以消除采样数据中多项式的趋势项。实际求得的位移为:
(9)
1.3 算法流程图
加速度采集电路选用DSP+FPGA的结构,在FPGA中实现控制A/D转化、计算加速度过载次数等功能,在高可靠性的32位定点DSP中完成加速度信号处理算法。其中,数据处理包括通过加速度数据的梯形积分得到位移信号,采用拟合多项式的方法去除趋势项等算法。程序设计包括初始化采集参数配置子程序、控制加速度采集子程序、加速度的时域积分算法和位移校正算法子程序、与主控系统的通信子程序、加速度过载次数计算子程序等。程序算法流程图如图3所示。
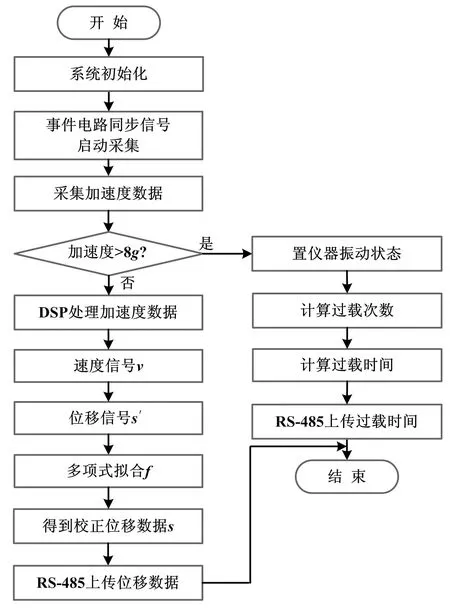
图3 程序算法流程图
Fig.3 Flowchart of program algorithm
系统上电以后,读取默认参数表中的采样率和采样点数N,采集加速度数据。随钻仪器在加速度为8g(g为重力加速度)以上的环境中工作时间不要超过20 min。当振动加速度大于8g以上的时间过长,就必须采取有效的措施消除振动后再进行测量[9],因此,需要判断振动加速度的大小,超过8g以上则计算过载时间并实时上传。如未超过8g,则在DSP中对加速度数据进行一次积分得到速度,再进行一次积分得到位移,利用多项式拟合的方法去除趋势项得到校正后的位移信号,通过RS- 485将位移数据实时上传至主控系统。
2 振动测试
2.1 测试环境
为了测试基于时域积分的加速度信号处理电路在振动条件下的位移测量性能,将振动测量系统的硬件部分固定在振动试验系统平台(振动平台系统型号:DC-5000-50)上进行扫频振动试验。振动试验系统框图如图4所示。
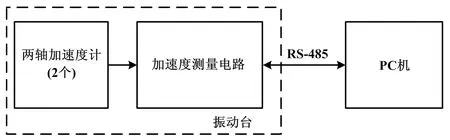
图4 振动试验系统框图
Fig.4 Block diagram of vibration test system
2.2 测试指标
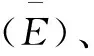
(10)
式中:X(t)为位移测量值;S(t)为位移理论值;max与min分别为位移的最大值与最小值;N为离散值点。
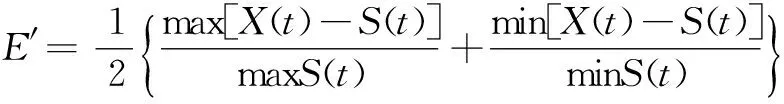
(11)
对于位移理论值与测量值的评价,在分析波形的总体效应时,波形代表能量的差值,可通过引入平方和误差(Ersq),来描述位移理论值与测量值能量的差别。
(12)
2.3 测试数据及分析
振动台上的扫频试验时间为30 min,加速度测量的采样率为fs=4 kHz,测量的数据点数为N=7.2×106个。振动试验台设定以5~30 Hz进行扫频,且将5~11.25 Hz时的位移限制在±1 cm范围内,将11.25~30 Hz时的加速度限制在±5g内。
加速度测量电路将加速度传感器采集的加速度信号数据通过串口RS- 485总线传到上位机,然后选取了某几段频率(扫频振动的频率为5 Hz、8 Hz和10 Hz)下的加速度数据,数据点数分别为4 096个。根据加速度时域积分算法,按照梯形公式对加速度一次积分得到速度信号曲线,再对速度信号进行一次积分得到位移曲线。然而,因为放大器的零点漂移以及加速度传感器的偏置,导致了二次积分后的位移信号上叠加有趋势项。为了消除趋势项,利用拟合多项式的方法,用最小二乘法拟合出趋势项误差。将上述积分后的位移减去与之对应的趋势项误差,即可获得位移的测量值曲线。其与振动台扫频试验获得的位移理论值曲线的对比如图5所示。
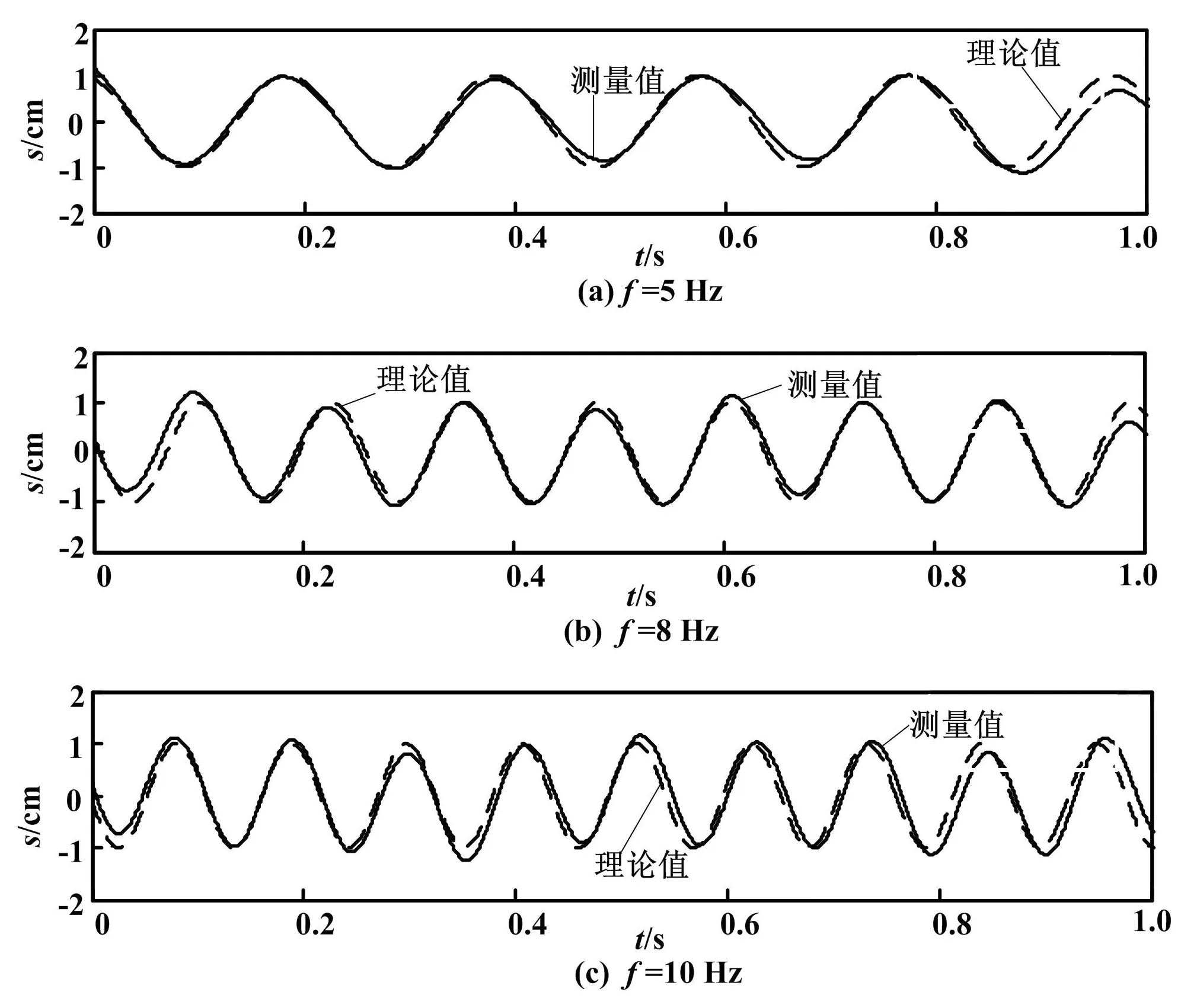
图5 不同频率下的位移测量值与理论值对比图
Fig.5 Measured values and theoretical values of displacement at different frequencies
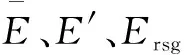
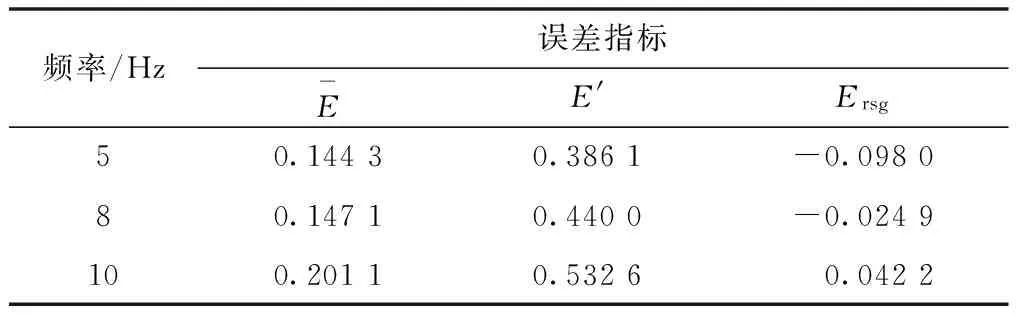
表2 不同频率下的积分位移误差对比Tab.2 Comparison of the displacement error of integration at different frequencies
从表2可以看出,各个频率下的误差大小变化不大且误差值较小,满足设计的要求。
3 结束语
本文设计了一个基于时域积分的加速度信号处理电路,分别采集了2个两轴的加速度值,并在高可靠性的32位定点数字信号处理器件DSP器件中完成了2次数值积分运算;然后采用拟合多项式极值方法,消除积分中产生的趋势项误差,得到了精确的位移值。振动测试试验表明:本设计的加速度测量电路所测得的位移值与实际振动台测量的理论值曲线相吻合,且误差较小。时域分析方法计算量小,能够实时性地分析井下仪器的运动状态,还可以避免由于傅里叶变换带来的截断误差,可广泛应用于随钻测井仪器的振动测量。
[1] COBERN M E,WASSELL M E.Laboratory Testing of an Active Drilling Vibration Monitoring & Control System[J].Gastips,2005(7):15-19.
[2] 祝效华,胡志强.基于钻头破岩钻进的下部钻具横向振动特性研究[J].振动与冲击,2014(17):90-93.
[3] ALVARADO R J,DAMGAARD A,HANSEN P,et al.Nuclear magnetic resonance logging while drilling[J].Oilfield Review,2003,15(2):40-51.
[4] 周小祥,陈尔奎,吕桂庆,等.基于数字积分和LMS的振动加速度信号处理[J].自动化仪表,2006,27(9):51-53.
[5] 吴志强,印娟,朱欣.MEMS加速度计嵌入式批量自动化测试系统设计[J].自动化仪表,2015,36(9):77-79,83.
[6] 周英杰.加速度测试积分位移算法及其应用研究[D].重庆:重庆大学,2013.
[7] YANG J,LI J B,LIN G.A simple approach to integration of acceleration data for dynamic soil-structure interaction analysis[J].Soil Dynamics and Earthquake Engineering,2006,26(8):725-734.
[8] 陈为真,汪秉文,胡晓娅.基于时域积分的加速度信号处理[J].华中科技大学学报(自然科学版),2010,38(1):1-4.
[9] 胡以宝,狄勤丰,邹海洋,等.钻柱动力学研究及监控技术新进展[J].石油钻探技术,2006,34(3):7-10.
[10]温广瑞,李杨,廖与禾,等.基于精确信息重构的故障转子系统振动加速度信号积分方法[J].机械工程学报,2013,49(8):1-9.
[11]蒋良潍,姚令侃,吴伟.边坡振动台模型试验动位移的加速度时程积分探讨[J].防灾减灾工程学报,2009,29(3):262-266.
LWD Vibration Acceleration Processing Circuit Based on Time-domain Integration
According to the vibration displacement of logging while drilling (LWD) instrument,the LWD data is evaluated,which is an effective method to improve measurement accuracy for the logging data.An acceleration signal processing circuit based on time-domain integration is researched and developed to measure the real-time vibration acceleration of LWD instrument,and then obtain the real-time vibration displacement by integral calculation.The high reliability 32 bit fixed-point DSP TMS320F2812 is selected to be the digital signal processing component; and the time domain integral method is selected to be the processing method for acceleration signal,because it takes less resource and is convenient for real-time calculation of micro system.Then,the method of fitted polynomial extreme value is used to eliminate the trend error generated in integration.The vibration test shows that the fitting accuracy for the displacement vs.time curve obtained by this acceleration measurement circuit and the curve of the theoretical values is higher,which can meet the demands for displacement measurement of LWD instrument.
Logging while drilling(LWD) Vibration acceleration Signal processing DSP Time-domain integration Fourier transform
高等学校博士学科点专项科研基金资助项目(编号:20130142120065)。
程晶晶(1977—),男,2011年毕业于华中科技大学控制科学与工程专业,获博士学位,讲师;主要从事低场核磁共振应用技术方向的研究。
TH86;TP216
A
10.16086/j.cnki.issn 1000-0380.201612001
修改稿收到日期:2016-05-09。
——信号处理

