抗差估计在变形监测数据处理中的应用

马 琳，邓文彬，张广泰

（1.新疆大学 建筑工程学院，新疆 乌鲁木齐 830046）

抗差估计在变形监测数据处理中的应用

马 琳1，邓文彬1，张广泰1

（1.新疆大学 建筑工程学院，新疆 乌鲁木齐 830046）

对抗差估计及其迭代初值进行了研究分析，并且针对不同估计方法所得到的迭代初值，利用Matlab对其进行模拟数据实验，对其“抗差性”进行比较，结合模拟结果选取“抗差性”较好的迭代初值进行下一步的抗差估计。最后利用某变形监测数据，同时采用最小二乘法和抗差估计两种方法进行比较，验证了抗差估计对粗差的“抗干扰性”。

抗差估计；M估计；变形监测；迭代初值；ρ函数

在变形监测工作中，不论采用何种精密测量仪器或测量方法，都有可能出现粗差[1,2]。粗差的出现，会使数据处理分析结果出现偏差，进而给后期的监测工作带来一定的困扰。在变形监测数据处理中，由于所测变形值很小，与观测中的误差极易混淆，这就要求在对数据进行处理分析时，尽可能避免或减小粗差对整体数据解算的干扰，以免影响对变形的正确分析[3]。

抗差估计与传统的统计方法相比，可以在数据中有粗差存在的情况下，减少粗差影响，从而得到具有“抗干扰性”的解算结果。本文以某工程项目的变形监测数据为基础，对其进行抗差估计分析，验证其对粗差的“抗干扰性”。

1 抗差估计

抗差估计是指在有粗差存在的情况下，选择合适的估计方法，尽可能降低粗差对未知量估值的影响，得出最优估值[1]。抗差估计基本上可分为3大类：M估计、L估计和R估计。本文中所用到的是M估计。

M估计是经典的极大似然估计的推广，称为广义极大似然型估计。

在对变形监测数据进行处理分析时，常采用线性回归法，若将抗差M估计与线性回归法结合在一起，可以有效抵抗粗差的干扰。

令φ（Vi）/Vi=Wi（权因子）为等价权元素，则有，将误差方程带入式（5），则有：

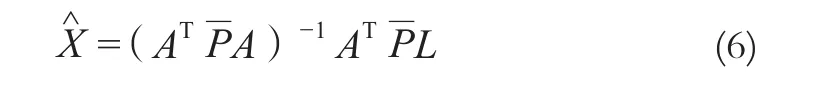
对式（6）的求解采用选权迭代法，选择合适的迭代初值解算参数第一次估值，由其解算出误差，进而确定新的等价权，得到下一次的参数估值，以此类推，直至前后两次解的差值符合一定的限差要求，即得到最终的参数估值[1,2,4]。

2 迭代初值以及ρ函数

抗差M估计的关键是选择合适的迭代初值和ρ函数。

2.1 迭代初值

2.1.1 最小二乘估计

目前一般都是采用最小二乘估计值来作为迭代初值，最小二乘估计的原理是最小化残差平方总和，即但由于最小二乘估计对粗差具有均衡作用，且对粗差不敏感，往往会降低抗差估计的抗差性[5,6]。

2.1.2 一次范数最小估计的线性规划算法

线性规划是研究线性约束条件下线性目标函数的极值问题的数学理论和方法，其数学模型为：

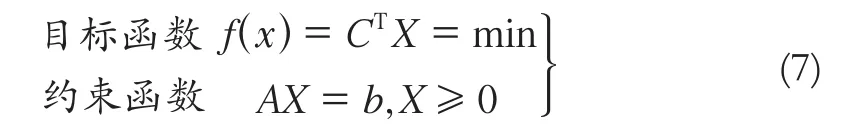
把X、V均视为待求参数，由于线性规划要求所有参数均为非负，而X、V可正可负，故设：

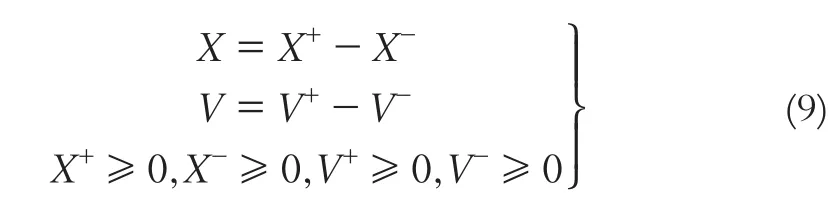
X+与X-、V+与V-互不独立，且不能同时存在非零解，则得到数学模型为：

即，

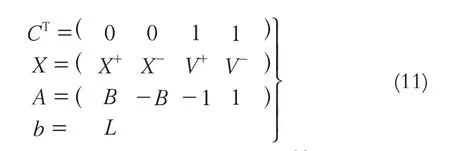
求解式（11），则可以得到X的估值[4]。

2.1.3 最小中位数平方

最小中位数平方的原理是最小化残差平方的中位数，即Median（）= min。最小中位数平方估值可以利用重复抽样算法来求解，其基本步骤为：从n个误差方程中随机抽取一个容量为p+1的子样本，其中p为自变量的维数，解算参数X，并计算p+1组的残差及其平方的中位数，选择残差平方中位数最小值所对应的参数估值为最终的抗差估值[7-9]。

2.2ρ函数

抗差M估计的对粗差的“抗干扰性”主要取决于迭代计算时所选取的ρ函数。一般情况下，ρ函数应尽量满足以下条件：

1）对称函数，即ρ（-v）= ρ（v）。

2）ρ（0）=0；ρ（v）在（-∞，0）区间上非增；ρ（v）在（0，-∞）区间上非降。

3）ρ（v）在（-∞，∞）区间上处处连续。

IGG法属于有淘汰区的M估计，权因子之间变化较平缓，同时这种估计方案充分考虑了测量数据的实际情况，是一种适合处理测量数据的抗差方案[1,10]。本文采用IGG法，其ρ函数及权函数为：

式中，u为标准化残差（ui= vi/σ）；ρ（u）为ρ函数；w （u）为权函数；b、c为调和系数，选取时可以参考有关文献推荐值[11]；d为常数；k为很小的数，避免u为0时出现计算问题[12]。

3 数据处理及分析

3.1 数据实验与分析

针对上文提到的3种迭代初值的计算方法，采用线性回归模型，利用Matlab进行模拟比较，选取较为合适的迭代初值。

采用模型yi= a1+a2xi+ε，令a1=5.0，a2=-2.9，模拟自变量x服从正态分布N （2，22），ε服从正态分布N（0，0.22），针对模型计算系数a1、a2，对于粗差，模拟分布yi～N（-3，0.52），j为粗差个数，实验数据为100个，粗差为30个，其模拟结果见表1。

表1 3种不同迭代初值计算结果比较

从表1可以看出，3种迭代初值计算方法中，最小二乘法对粗差的抗干扰能力比较弱，其余两种方法均可以较好地抵抗粗差。本文采用最小中位数平方估值作为迭代初值，进行下一步抗差估计。

3.2 变形观测数据的处理及分析

本文选取某工程的变形观测数据，对其进行抗差线性回归分析，原始数据如表2。

表2 原始数据

利用Matlab画出散点图，依据散点图选用指数模型y=a×eb/x对其进行抗差线性回归分析。由于指数模型本身不是线性模型，故先将指数模型线性化：y=a×eb/x⇒（lny）=（lna）+b×（1/x），然后利用后面线性化后的模型进行数据处理与分析。

若在第4、8、12、16天的下沉量上各加入2、5、7、9 mm的粗差，采用常用的最小二乘法对其进行线性回归，同时采用以最小中位数平方估值作为迭代初值，以IGG法作为权函数的抗差估计与其进行对比，结果如图1所示。

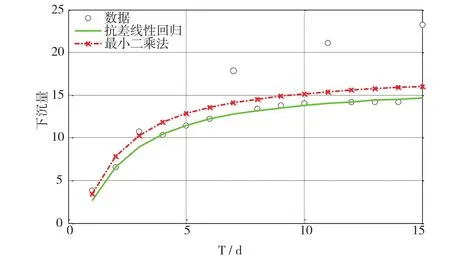
图1 最小二乘法与抗差估计绘制的拟合结果图

从图1可以直接看出，在有粗差存在的情况下，采用的最小二乘法所绘制出来的拟合图已经完全偏离了真实数据，偏向有粗差的数据；而抗差估计计算绘制出来的拟合图则没有受到粗差数据的影响，正确预测出了变形数据的趋势。从表3中的各项指标数据中也可以看出，最小二乘法的解算结果没有抗差估计的解算结果好。

表3 数据处理结果

4 结 语

常用的最小二乘法在有粗差存在的情况下，所得的估值有一定的偏差，而抗差估计则可以在有粗差存在的情况下，仍然对其进行无偏估计。所以将抗差估计应用在变形监测的数据处理中，不但可以对其进行分析预测，还可以使其在有粗差的情况下，避免粗差对分析预测结果产生干扰。但是在变形监测数据处理中，影响因素往往有多个，而本文中所用到的变形监测数据只有一个影响因素，若将抗差估计应用在有多个影响因素的变形监测数据处理中，则抗差估计的结果可能会更好，这还有待进一步的验证研究。

[1] 周江文,黄幼才,杨元喜．抗差最小二乘法[M]．武汉∶华中理工大学出版社,1997

[2] 杨元喜．抗差估计理论及其应用[M]．北京∶八一出版社,1993

[3] 康世英,张宏伟．变形观测数据处理粗差的定位与剔除[J]．桂林工学院学报,2003,23(3)∶310-313

[4] 刘大杰,陶本藻．实用测量数据处理方法[M]．北京∶测绘出版社,2000

[5] Andersen R．现代稳健回归方法[M]．上海∶格致出版社,2012

[6] 邱卫宁．具有稳健初值的选权迭代法[J]．武汉大学学报∶信息科学版,2003,28(4)∶452-454

[7] 王海娜．线性回归模型的若干稳健估计方法及应用实例[D]．济南∶山东大学,2013

[8] 杨玲,沈云中,楼立志．基于中位参数初值的等价权抗差估计方法[J]．测绘学报,2011,40(1)∶28-31

[9] 王彤,王琳娜,何大卫．基于LMS回归的一步M估计与加权最小二乘估计[J]．现代预防医学,1996,26(3)∶281-283

[10] 周江文．经典误差理论与抗差估计[J]．测绘学报, 1989,18(2)∶115-120

[11] 李浩军,唐诗华,黄杰．抗差估计中几种选权迭代法常数选取的探讨[J]．测绘科学,2006,31(6)∶70-72

[12] 贾超．稳健回归分析方法在变形监测中的应用[D]．太原∶太原理工大学,2011

P258

B

1672-4623（2016）01-0089-03

10.3969/j.issn.1672-4623.2016.01.026

马琳，硕士，主要研究方向为大地测量、工程测量。

2014-12-31。

项目来源：国家自然科学基金资助项目（51368056）；武汉大学精密工程与工业测量国家测绘地理信息局重点实验室开放基金资助项目（PF2012-20）；新疆大学校院联合基金资助项目（XY110135）。