关于高程系统的思考
许厚泽
(1.中国科学院 测量与地物理研究所,湖北 武汉430077)
关于高程系统的思考
许厚泽1

讨论了3种高程系统(正高、正常高及区域正常高)及其区别,它们分别依赖于不同的基准面,即大地水准面、似大地水准面和区域似大地水准面;研究了如何把中国的区域高程系统转换为全球统一高程系统的2种途径。可以利用水准或重力方法、GPS水准和GPS重力方法建立高程系统。
高程系统;正常高;大地水准面;GPS水准
通常,人们把高程定义为地面点到全球平均海平面(大地水准面)的垂直距离,这样定义的高程叫做正高。习惯上,高程测量是用水准测量完成的,但水准测量得到的点是两点间重力位之差(重力位的定义为地球质量作用于此两点的引力位及地球自转导致的同一点的离心力位之和),因此高程的定义与地球的重力位密切相关。
1 高程系统
当前,世界上对高程有3种定义,相应的有3种高程系统(图1)。

图1 3种高程系统示意图
1.1 正高HA
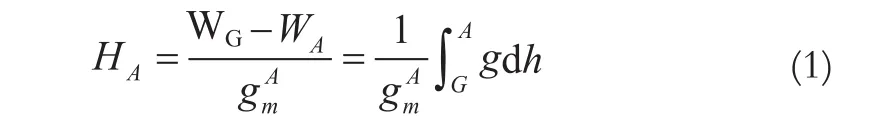
式中,HA表示地面点沿垂线到大地水准面的距离AAG;WG是大地水准面的重力位,由于大地水准面是一个等位面,WG为常数;WG-WA为地面点A和大地水准之间的重力位差,可从重力测量或水准测量(由大地水准面上任意点沿任意水准线测到A点给出的得到;g及dh为G到A水准线上的重力及高差;是点A沿垂线到大地水准面的平均重力值。
基于正高的高程系统称为正高高程系统,其依据的高程基准面为大地水准面。

G'得的点G'的集合形成的面就定义为似大地水准面,显然,似大地水准面是人为定义的,不具备任何物理意义,也不是等位面。式(2)不同于式(1),用点A沿地球椭球法线到似大地水准面的平均重力值来代替。由于正常重力可根据地球椭球参数准确求得,因此,理论上,正常高是可以精确测量的。
基于正常高的系统称为正常高高程系统,其依据的高程基准面为似大地水准面。
实际上,由式(2)按水准测量测量正常高时,人们并不知道地球上哪一点的正常高为零,一般取沿海某验潮站某历元(如我国采取青岛1985年)的平均海平面作为水准原点。但这个水准原点并不在大地水准面上,它的重力位并不等于WG,因此,在实际应用上,采用区域正常高系统来代替正常高系统。
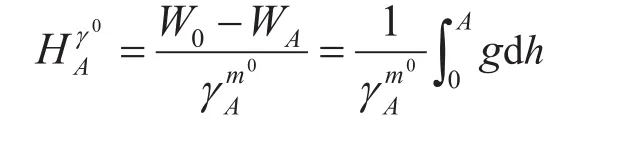
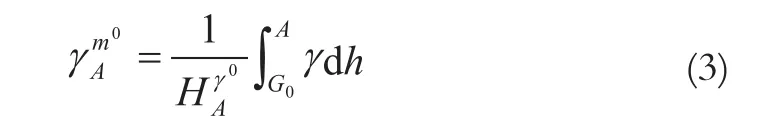
基于区域正常高的高程系统称为区域正常高高程系统,这一系统明显依赖于水准起始原点的重力位W0。
2 3个高程基准面之间的关系
1)大地水准面与似大地水准面的差别为:
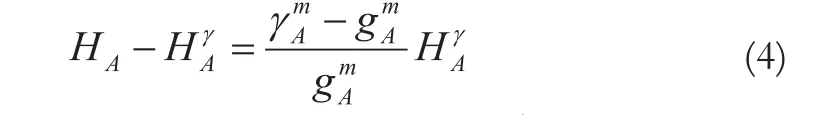
2)似大地水准面与区域似大地水准面的差别为:
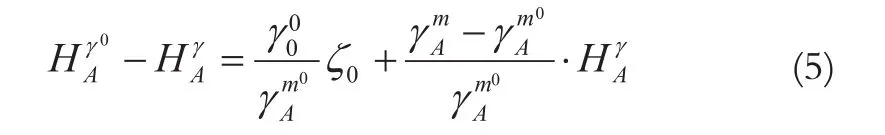

换言之,这两个面近似地可认为是平行的,其差距ζ0为青岛原点的似大地水准面高程异常,约为0.3 m。同样,海洋上区域似大地水准面就是通过青岛原点的平均海平面,其距似大地水准面或大地水准面的距离等于ζ0。式(6)表明只要知道区域似大地水准面高程系统水准原点外的ζ0,就能很容易转化为全球似大地水准面高程系统。
3 建立高程基准的途径
如前节所述,正高理论上是无法精确确定的,人们只能由正常高近似求得。这里仅讨论建立正常高系统(似大地水准面基准)及区域正常高(区域似大地水准面基准)的方法。除去水准测量方法外,现在人们很容易从GPS求得地面点的大地高h(地面点到地球椭球面的距离),从而根据定义,可以有不同途径来建立高程系统。
1)水准测量方法。
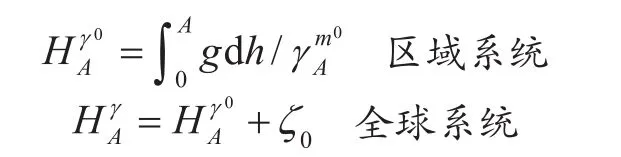
2)GPS水准方法。

3)GPS重力方法。

4)GPS水准加GPS重力拟合方法。拟合时,如果GPS水准观测值权取为无穷大,即GPS水准方法;如把重力大地水准面权取为无穷,即GPS重力方法。
综上所述,就亚mm级精度的高程系统而言,利用水准测量,可直接建立区域似大地水准面高程系统,要转变为全球系统,需要精确测定出水准原点处的似大地水准面高程异常ζ0,利用GPS代替水准测量,如果有精化的区域似大地水准面高程异常ζA0,可以直接建立区域似大地水准面全球系统。同样,要转变为全球系统,要知道ζ0,如果有精化的似大地水准面高程异常ζA,可以直接建立全球似大地水准面高程系统,而要转变为区域系统,要知道ζ0。
4 建立未来中国高程基准的思考
当前我国高程基准是基于水准测量或GPS结合精化GPS水准区域似大地水准面。该基准存在以下问题:
1) 不是全球的系统,而是取决于青岛验潮站的区域型系统。
2)依赖于水准测量,从而有很大的误差积累,仅以一等水准为例,要从青岛传递到西安,高程绝对误差将达到±6~7 cm。
3)以GPS水准为主精化的区域似大地水准面的精度估计,存在局限性,尤其在山区,可供使用的检测点太少。
为了进一步完善我国未来的高程基准,迫切需要探讨以下的问题:
1)建立一个基于GPS和全球重力似大地水准面的高程基准。
这是一个很大的课题。首先,要研究在给定的精度要求下(如在我国沿海及平坦地区绝对精度达到±2~3 cm,山区达到±5~7 cm)重力观测值的分布、密度以及实现的途径。当前从可用的重力资料来看,中长波长及沿海海域,可以使用卫星重力及卫星测高的结果,难点在于高分辨率格网的资料。东中部地区基本已能满足,只需适当加密;关键在西部,最有效方法应该要启动航空重力测量,既快速又高效。其次,在理论与计算方法方面,要研究选用不同理论(莫洛金斯基参数展开、Moritz解析延拓、Stokes-Helment质量压缩等)对计算结果(尤其在山区)的影响以及地形资料的使用问题。最后,还涉及全球参数的选择,包括地球参考椭球、ITRF参考框架、大地水准面位值WG(与地心引力参数GM相关)、潮汐系统等。
2)研究以cm级精度确定青岛原点似大地水准面高程异常ζ0的方法,从而把当前我国的区域高程系统转换为全球系统,并与GPS重力的结果相比较。目前,最可行方法是用最新的重力场模型(如EIGEN-6Cd)和中国沿海及东部GPS水准点相比较,在比较时,同样要注意重力模型和GPS系统中所用全球参数的问题。
[1] Heiskanen W A,Moritz H,Freeman W H. Physical Geodesy[M]. San Francisco, 1967
[2] 许厚泽.我国精化大地水准面工作中若干问题的讨论[J].地理空间信息 ,2006,4(5)∶1-3
[3] Hsu H T, Lu Yang. The Regional Geopotential Model in China[J].Bollettino di Geodesia e Scienze Affini,1995(2)∶161-175
[4] Wang Y M. Downward Continuation of the Free-air Gravity Anomalies to the Ellipsoid Using the Gradient Solution, Poisson's Integral and Terrain Correction-Numerical Comparison and Computations[R]. OSU Report,1988
[5] Featherstone W. Refinement of Gravimetric Geoid Using GPS and Leveling Data[J].Journal of Surveying Engineering, 2000,126∶27-56
[6] 李建成,陈俊勇,宁津生,等.地球重力场逼近理论与中国2000似大地水准面的确定[M]. 武汉∶武汉大学出版社,2001
[7] 郭东美,许厚泽.基于方差分量估计的局部似大地水准面精化拟合模型[J].地球物理学进展,2011,26(3)∶813-818
我国高程基准的发展历史
地球表面某一点的空间位置可以用该点的经度、纬度和高程来表示。经纬度用来表示该点平面位置。那么,高程是从哪里开始作为起点呢?人们自然地会想到用海平面来作为起算基准面,进而得到陆地上某点相对海平面的高度,即为“海拔”。据《元朝名臣事略》记载,元朝著名科学家郭守敬对此就进行过科学的实践,他曾用海平面来比较大都(今北京市)与汴梁(今河南开封市)的地势高低之差,认为汴梁的河流水面高出海平面较多,因此流速较快;而大都的河流水面高出海平面较少,故而流速较慢。这是我国历史上第一次提出利用海平面作为基准来比较不同地区的“海拔”的科学思想。这一科学思想一直沿用至今,目前国内外的高程参考面仍是以平均海平面作为基准面。
在新中国建立前,我国曾在吴淞、青岛、大连、大沽、坎门和广州等地建立高程基准点。其中“吴淞零点”是我国近代最早的高程基准点。1860年,清朝的上海海关巡工司在黄浦江西岸的张华浜设立了水位观测站。利用1871~1900年的长期水位观测资料,确定了一个比当时实测最低水位略低的高程作为水尺零点,称之为“吴淞海关零点”,后正式更名为“吴淞零点”。除“吴淞零点”外,其他大部分高程基准点的建立,多与帝国主义列强的入侵有关。
建国初期,我国选择了地质结构较为稳定的青岛验潮站为基本验潮站,并以该验潮站1950~1956年7 a的观测资料获得平均海平面,作为我国高程的统一起算基准,即为“1956黄海高程系统”。这也是新中国第一个国家高程系统,彻底结束了过去高程系统繁杂的局面。由于计算“1956黄海高程系统”所依据的青岛验潮站的资料时间相对较短。随着观测资料的累积和观测精度的提高,国家测绘地理信息局决定以青岛验潮站1952~1979年的潮汐观测资料为计算依据,重新确定了新的国家高程基准,称为“1985国家高程基准”,并在青岛观象山上构建了“中华人民共和国水准原点”。该水准原点在“1985国家高程基准”中的高程是72.260 m,在“1956黄海高程系统”水准原点的高程是72.289 m,二者相差0.029 m。水准原点建成后,我国相继开展了多次全国一等和二等水准网的建设与观测,为我国的经济建设、国防安全和科学研究提供了全国统一且精确可靠的高程基准。
由于各国采用的作为高程基准面的平均海平面是不一致的,我国“1985国家高程基准”也不例外,因此,统一全球的高程系统现已成为大地测量学中一项重要课题。
(冯伟:中国科学院测量与地球物理研究所 大地测量与地球动力学国家重点实验室)
P224
B
1672-4623(2016)01-0001-03
10.3969/j.issn.1672-4623.2016.01.001
许厚泽,中国科学院测量与地物理研究所研究员,中科院院士,从事大地测量及重力测量学研究。
2015-11-24。
项目来源:国家自然科学基金资助项目(41131067)。

