一类加法补集问题的研究

刘鑫媛，方金辉

(南京信息工程大学数学与统计学院，江苏 南京 210044)

一类加法补集问题的研究

刘鑫媛，方金辉

(南京信息工程大学数学与统计学院，江苏 南京 210044)

加法补集；计数函数；上极限

1 预备知识

设A和B是无穷正整数集合.若它们的和A+B={a+b|a∈A，b∈B}包含所有充分大的整数，则称A，B为加法补集.设A(x)和B(x)分别是集合A和B中不大于x的元素个数，即

1964年，Danzer[1]提出猜想：对于加法补集A，B，若

则

A(x)B(x)-x→∞，x→∞.

A={0+2a2+4a4+…+2sa2s，2i=0，1，…，a-1；s=0，1，2，…}，

B={1a+3a3+5a5+…+2s-1a2s-1，2i-1=0，1，…，a-1；s=1，2，…}，

2 主要结论及证明

本文对于上述加法补集A与B，当a=2时给出了满足A(x)B(x)-x=1的所有正整数x，结论如下：

定理1 设加法补集

A={0+222+424+…+2s22s，2i=0，1；s=0，1，2，…}，

B={12+323+525+…+2s-122s-1，2i-1=0，1；s=1，2，…}.

对于正整数x，A(x)B(x)-x=1的充要条件是x=2k-1，其中k是正整数.

定理2 存在加法补集A与B，使得对任意正整数k，A(x)B(x)-x=k对于无限多个正整数x均成立.

定理1的证明 先证充分性.由文献[4]，当x=22k-1时，A(x)B(x)-x=1.类似可得，当x=22k-1-1时，A(x)B(x)-x=1.充分性得证.

再证必要性.对任意正整数x，分以下两种情况讨论.

情形Ⅰx=η0+η12+η222+…+η2k-122k-1+22k，其中ηi=0或1.此时显然B(x)=2k.

若x=22k，则A(x)=2k+1.此时由A(x)B(x)-x=1可得k=0，故x=1=21-1，从而只需讨论x=η0+η12+η222+…+22m-1+22k(其中1≤m≤k)和x=η0+η12+η222+…+22m+22k(其中0≤m≤k-1)这两种情况.

(1)x=η0+η12+η222+…+22m-1+22k，其中1≤m≤k.此时A(x)≥2k+2m，因此

A(x)B(x)-x≥(2k+2m)2k-(20+21+…+22m-1+22k)=

22k+2k+m-(22m-1+22k)=2m(2k-2m)+1.

由上式，若A(x)B(x)-x=1，则2k-2m=0(即k=m)，A(x)=2k+2m和x=20+21+…+22m-1+22k同时成立.综上所述，若A(x)B(x)-x=1且x=η0+η12+η222+…+22m-1+22k，则

x=20+21+…+22k-1+22k，

即x=22k+1-1.

(2)x=η0+η12+η222+…+22m+22k，其中0≤m≤k-1.此时A(x)≥2k+2m，因此

A(x)B(x)-x≥(2k+2m)2k-(20+21+…+22m+22k)=

22k+2k+m-(22m+1-1+22k)=2m(2k-2m+1)+1.

由上式，若A(x)B(x)-x=1，则2k-2m+1=0(即m=k-1)，A(x)=2k+2m和x=20+21+…+22m+22k同时成立.而当x=20+21+…+22k-2+22k时，A(x)=2k+1，得出矛盾.

情形Ⅱx=η0+η12+η222+…+η2k-222k-2+22k-1，其中ηi=0或1.此时显然A(x)=2k.

若x=22k-1，则B(x)=2k-1+1.此时由A(x)B(x)-x=1可得k=0，与k是正整数矛盾.所以只需讨论x=η0+η12+η222+…+22m+22k-1(其中0≤m≤k-1)和x=η0+η12+η222+…+22m-1+22k-1(其中1≤m≤k-1)这两种情况.

(1)x=η0+η12+η222+…+22m+22k-1，其中0≤m≤k-1.此时B(x)≥2k-1+2m，因此

A(x)B(x)-x≥2k(2k-1+2m)-(20+21+…+22m+22k-1)=

22k-1+2k+m-(22m+1-1+22k-1)=2m(2k-2m+1)+1.

由上式，若A(x)B(x)-x=1，则2k-2m+1=0(即m=k-1)，B(x)=2k-1+2m和x=20+21+…+22m+22k-1同时成立.综上所述，若A(x)B(x)-x=1且x=η0+η12+η222+…+22m+22k-1，则

x=20+21+…+22k-2+22k-1，

即x=22k-1.

(2)x=η0+η12+η222+…+22m-1+22k-1，其中1≤m≤k.此时B(x)≥2k-1+2m-1，因此

A(x)B(x)-x≥2k(2k-1+2m-1)-(20+21+…+22m-1+22k-1)=

22k-1+2k+m-1-(22m-1+22k-1)=2m(2k-1-2m)+1.

由上式，若A(x)B(x)-x=1，则2k-1-2m=0(即m=k-1)，B(x)=2k-1+2m-1和x=20+21+…+22m-1+22k-1同时成立.而当x=20+21+…+22k-3+22k-1时，B(x)=2k，得出矛盾.

定理2的证明 设

A={0+222+424+…+2s22s，2i=0，1；s=0，1，2，…}，

B={12+323+525+…+2s-122s-1，2i-1=0，1；s=1，2，…}.

容易验证A与B是加法补集.

对任意正整数k，存在无限多个正整数m使得

因此

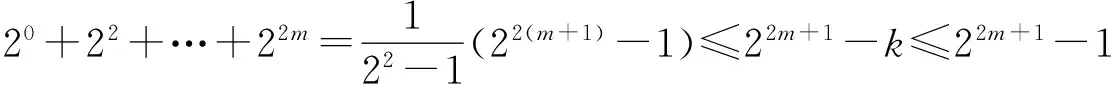
(1)

令x=22m+1-k，注意到

20+22+…+22m≤x≤22m+1-1，

有A(x)=2m+1.由(1)式可得

从而B(x)=2m.

综上，

A(x)B(x)-x=22m+1-(22m+1-k)=k，

定理2得证.

[1] DANZER L.Übereine fragevong hanani aus der additiven Zahlentheorie[J].J Reine Angew Math，1964，214/215(1)：392-394.

[3] FANG JINHUI，CHEN YONGGAO.On additive complements[J].Proc Amer Math Soc，2010，138(6)：1923-1927.

[4] CHEN YONGGAO，FANG JINHUI.On additive complements Ⅱ[J].Proc Amer Math Soc，2011，139(3)：881-883.

[5] FANG JINHUI，CHEN YONGGAO.On additive complements Ⅲ[J].J Number Theory，2014，141：83-91.

(责任编辑：李亚军)

On a problem of additive complements

LIU Xin-yuan，FANG Jin-hui

(School of Mathematics and Statistics，Nanjing University of Information Science and Technology，Nanjing 210044，China)

additive complements；counting functions；upper limit

1000-1832(2016)04-0024-03

10.16163/j.cnki.22-1123/n.2016.04.006

2015-07-07

国家自然科学基金资助项目(11671211)；江苏省高校研究生科研创新计划项目(KYLX15_0884).

刘鑫媛(1991—)，女，硕士，主要从事数论研究.

O 189.1 [学科代码] 110·17

A