基于Nios Ⅱ的脉冲神经网络硬件实现方法
张文娟,王 蕾,王连明
(东北师范大学物理学院,吉林 长春 130024)
基于Nios Ⅱ的脉冲神经网络硬件实现方法
张文娟,王 蕾,王连明
(东北师范大学物理学院,吉林 长春 130024)
将脉冲神经网络的理论和算法应用于函数拟合研究,通过使用Cyclone Ⅱ EP2C35F672C8N型FPGA芯片和基本外围电路,并基于Nios Ⅱ软核技术,建立了脉冲神经网络硬件模型.以指数函数为例拟合曲线,系统训练结束后稳定误差可达到0.2.实验结果表明,基于Nios Ⅱ的硬件实现方法能够成功地实现脉冲神经网络,为人工神经网络的研究提供了有效的仿真平台,同时该方法能够有效地模拟连续函数,扩展了神经网络的应用领域.
脉冲神经网络;硬件实现;Nios Ⅱ;曲线拟合
近年来,人工神经网络在信号处理、人工智能、医疗、控制系统、模式识别等领域中得到了广泛的应用.目前,基于计算机的软件仿真是人工神经网络实现的主要方法,它具有应用灵活且不需要专用硬件等优点,但无法应用在某些对体积、稳定性、功耗等要求严格的嵌入式领域.因此,人工神经网络硬件实现是神经网络发展的必然趋势,其硬件实现技术也将成为研究的热门课题.
1 神经网络的硬件实现方法
人工神经网络硬件实现方法的研究成果众多[1],主要有基于电子技术和基于光电子技术两种实现方法.由于电子技术的快速发展,绝大多数神经网络是基于电子技术硬件实现的,它可以分为基于通用处理器单元的神经计算方法和基于超大规模集成电路(VLSI)的神经芯片方法.其中基于VLSI技术的实现方法包括模拟方法、数字方法和数模混合方法[2].
(1)神经网络的数字实现方法具有精度高、灵活性大、工艺成熟、易于存储和权值更新等优点,但缺点是电路规模大、集成电路的几何尺寸大、集成难度大,而且成本高[3].
神经网络的模拟实现方法优点是突触和神经元电路易于集成,和外界易于接口,但缺点是对器件参数的变化敏感,权值的存储和修改十分困难[4-5].
(2)神经网络的数模混合方法优点在于具有数字实现的灵活性,易解决大批量权值的快速存储和修改问题,同时又兼有模拟实现的乘加电路简单的特点,是较理想的实现通用神经网络的途径.但该方法中模拟信号和数字信号之间需要DAC和ADC电路,因此电路规模较大.
自从Murray和Smith在1987年将脉冲技术用于神经网络的VLSI实现以来,神经网络的脉冲技术实现引起人们的关注[6-7].脉冲技术是将神经元状态编码调制在脉冲波形上,可用脉冲宽度的变化PWM或脉冲频率的变化PFM来表示神经元的状态.脉冲信号可以简化运算电路(例如突触电路)使神经元间有较高的互联密度,也可以使神经芯片与数字电路及计算机的其他外围设备易于接口.用脉冲技术实现神经网络,可融合模拟和数字技术两者的优点,是一种较好的神经网络实现方法.
2 脉冲神经网络
近年来,脉冲神经网络的研究越来越受到人们的重视.该神经网络是直接利用精确的脉冲发放时间对数据进行处理,而传统的神经网络模拟的是生物神经元的脉冲发放频率,因而脉冲神经网络更接近于真实的生物系统,更加符合生物信息处理机制.
2.1 脉冲神经元模型

图1 I&F神经元模型
脉冲神经元模型是更接近生物神经元的一个数学模型.传统的Sigmoid神经元模型是将一个实数输入,再通过传递函数转换成一个实数输出.而脉冲神经元模型则不同,该模型的本质是当脉冲神经元受到外界的刺激,膜电位会升高,当其超过阈值电压时,该神经元产生一个脉冲,并发送一个输出信号.在脉冲神经网络中常见的神经元模型有I&F(Integrate and Fire)模型、LI&F(Leaky Integrate and Fire)模型、H-H(Hodgkin-Huxley)模型、SRM(Spike response model)模型等.综合比较发现,I&F模型能够更好地获得神经系统的动态特性,且实现相对比较简单,因此本文采用的是I&F神经元模型.该模型基本电路如图1所示[8].

I&F模型的原理电路是由电流I(t)驱动一个电容C和一个电阻R组成.驱动电流可以分成2个部分,I(t)=IR+IC.IR是通过线性电阻器R的电阻电流,它可以根据欧姆定律IR=u/R计算,u是电阻两端的电压.IC为电容C充电,从C=q/u(q是电荷)得出IC=Cdu/dt.因此有
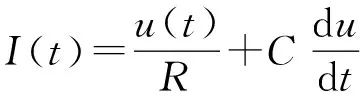
(1)
(1)式子两端都乘以R,并引入积分时间常数项τm=RC,得出标准方程
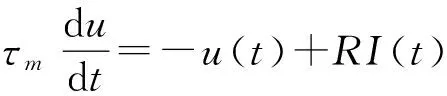
(2)
为了对I&F神经元模型进行精确的事件驱动模拟,本文假设积分发放神经元由一个恒定输入电流I(t)=I0刺激,复位电压ur为0.假设在t=t(1)时,一个尖峰发生.根据(2)式和初始条件u(t(1))=ur=0得出膜电压的轨迹,即
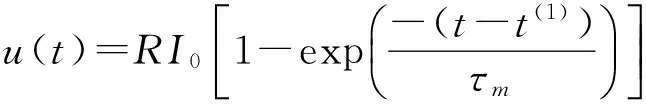
(3)

2.2 脉冲神经网络的学习算法
大脑具有很强的学习记忆功能,它是基于神经元间的突触可塑性,即突触前后神经元内部连接强度自适应的改变能力.对应到神经网络中,这就涉及突触权值和阈值的改变.STDP(Spike Time Dependent Plasticity)规则是一种突触可塑性规则,它与前后神经元发放脉冲时间顺序息息相关[9-10],其时间依赖性理论更接近生物特性,且在目前应用比较广泛,因此本文采用该学习算法.
STDP利用相连的脉冲神经元发放脉冲的时间差信息对突触权值进行修改,其数学模型为:
(4)
(5)

3 Nios Ⅱ软核处理器
Nios Ⅱ[11]是一种通用流水线型的RISC处理器内核的软核处理器,等同于微控制器或者“片上计算机”.Nios Ⅱ处理器系统是将Nios Ⅱ处理器核、片内外设集合、片内存储器和片外接口等集成在一块单一的FPGA芯片上.所有的Nios Ⅱ处理器系统使用统一的指令集和编程模型.
因为FPGA器件的引脚和逻辑资源是可编程的,可以实现许多用户自定义的特性.同时,用户能够重新安排芯片上的引脚,因此在电路板设计上更加容易、灵活.片上额外的引脚和逻辑能用来为Nios Ⅱ处理器系统实现附加的外设和硬件逻辑.
本文采用的FPGA芯片是Cyclone Ⅱ 系列的EP2C35F672C8N.经过实验验证,该器件资源符合存储计算功能要求.器件主要参数见表1.

表1 Cyclone Ⅱ EP2C35F672C8N参数表
4 实验过程和结果
本文基于Nios Ⅱ处理器采用脉冲神经元构造了一个三层的指数曲线函数神经网络模型,具体实现过程如下:
(1) 在Quartus中使用SOPC Builder搭建软核处理器系统;
(2) 在Nios Ⅱ IDE中实现脉冲神经网络模型,并将实验数据通过串口输出;
(3) 用脉冲神经网络输出的实验数据绘图.
4.1 搭建软核处理器系统
在Quartus软件中使用SOPC Builder建立软核处理器系统,使用的ip核包括标准型cpu、片上32K ram、uart和8位pio输出口,如图2所示.图2中uart是RS-232串口控制软核,网络运行结束后将计算结果通过串口显示.8位pio输出口用于显示网络计算过程中运行的标志和状态.

图2 软核处理器系统
4.2 Nios Ⅱ IDE中实现的脉冲神经网络模型
在Nios Ⅱ IDE中实现拟合指数曲线函数的脉冲神经网络模型.该模型主要包含信息编码层、处理层和输出层.信息编码层主要接收函数输入值,并将其转化为具有不同发放时间的脉冲序列;处理层主要是将上一层输出的脉冲序列送入神经元组成的处理网络;输出层则将处理层的处理结果以数组的形式输出.
(1) 信息编码层
脉冲神经网络的输入输出是脉冲序列,因此不能直接进行模拟量的计算,必须要先将模拟量编码为脉冲序列后再作为神经网络的输入.本文采用线性编码方式,将函数输入x转化成脉冲发放时间n,如(6)式所示.其中,时间窗设定为20 ms,x取20个点,取值范围是-1.2~6.根据要拟合的函数y=ex计算,实际函数范围是0.301 194~403.428 793.将理想的输出时间也同样转化到时间20 ms内,理想输出为:
(6)
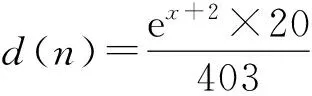
(7)
(2) 处理层
实验中脉冲神经网络采样时间为0.01 s,时间窗为20 ms,即共采样2 000次.分别将信息编码层输出的20个脉冲信号时间上加宽0.04 s作为网络输入,实验证明此处理方法有利于电压信号累积,累积达到1.2 V时发放脉冲,记录发放时间并作为临近的脉冲输入信号的计算结果,实现了将脉冲序列转换成脉冲电压信号,再基于STDP规则更新网络权值,本文中学习率取值为A+=1,A-=0.5,时间参数取值为τ+=20,τ-=50,保证A-τ->A+τ+整体范围内学习强度减弱.
(3) 输出层
由于网络输入和理想输出是经过编码实现的,因此实际输出结果也要经过解码才能与实际输入对应.解码公式为

(9)
其中u(n)为对应输入脉冲n的发放脉冲的时间,y(x)表示对应输入的实际输出值.最后网络将实际输入和实际输出通过串口输出,网络计算过程中首次数据结果见图3.图3中n表示网络输入的脉冲时间,d表示函数期望值,u表示实际输出的电压脉冲值,w表示网络权值,e表示误差.

图3 串口调试助手接收实验数据
4.3 实验结果
实验数据见图4.实际输入x=[-1.2,0,0.5,1.4,1.8,2.1,2.2,2.3,3.1,3.5,4,4.2,4.3,4.4,4.7,5.2,5.7,5.8,5.9,6],共20个数值,经过脉冲神经网络的信息编码层处理后转化成脉冲发放时间n,n=[1.777 8,4.444 4,5.555 6,7.555 6,8.444 4,9.111 1,9.333 3,9.555 6,11.333 3,12.222 2,13.333 3,13.777 8,14.000 0,14.222 2,14.888 9,16.000 0,17.111 1,17.333 3,17.55 56,17.777 8],脉冲幅值为1,见图4(a),其横坐标表示时间,纵坐标表示脉冲幅值.脉冲神经网络运行过程中输出电压根据输入脉冲的刺激,不断出现累积和发放的现象,见图4(b),其横坐标表示时间,纵坐标表示输出电压值.网络共运行了50次,更新了50次权值,网络训练后的实际输出结果和函数期望值见图4(c),其横坐标表示实际输入值,纵坐标表示函数期望值和输出值.网络实际输入共20个点,图4(d)给出了其中一个点n=8.444 4 的运行过程中误差的变化规律,其横坐标表示网络运行次数,纵坐标表示误差.网络中其他各点误差变化趋势大体相同.通过计算数据得出,网络训练结束后实际输出值与函数期望值平均误差值为0.3.

(a)网络输入的脉冲信号

(b)网络输出的电压脉冲信号

(c)训练结束后实际输出值与期望值

(d)网络中n=8.444 4的误差变化
图4 实验数据
5 结论
本文提出了一种基于Nios Ⅱ的脉冲神经网络的硬件实现方法,完成了网络建模,并以拟合指数函数为例给出了实验结果.整个系统具有器件少、成本低、灵活性强、数据存储方便、开发周期短等众多优点,对促进神经网络乃至智能信息处理技术的发展具有重要的工程实践价值.同时解决了多数脉冲神经网络在图像处理方面的应用缺点,而将其扩展到模拟连续函数等问题上,扩展了神经网络的应用领域,具有一定的理论研究价值和现实意义.
[1] 程丹,王连明.基于NIOS Ⅱ多核技术的Hopfield神经网络硬件实现方法[J].东北师范大学(自然科学版),2011,43(3):65-68.
[2] 陈琼,郑启伦.人工神经网络系统硬件实现的研究进展[J].电路与系统学报,2000,5(1):48-51.
[3] TAKAO WATANABE,KATDUTAKA KIMURA,MASAKAZU AOKI,et al.A single 1.5-V digital chip for a 106 synapse neural network [J].IEEE Transactions on Neural Networks.1993,4(3):387-393.
[4] 高丽娜,邱关源.一种连续可调权值CMOS 神经网络[J].电子学报,1998,26(2):120-122.
[5] LINARES-BARRANCO,SANCHEZ-SINENCIO B,RODRIGUEZ-VAZQUEZ E,et al.A modulart-mode design approach for analog neural network hardware implementations [J].IEEE Journal of Solid-State Circuits,1992,27(5):701-712.
[6] YASUHIRO OTA,BOGDAN M WILAMOWKI.Analog implementation of pulse-coupled neural networks [J].IEEE Transactions on Neural Networks,1999,10(3):539-544.
[7] EZZEL-MASRY,YANG H-K,YAKOUT M A.Implementations of artificial neural networks using current-mode pulse width modulation technique [J].IEEE Transactions on Neural Networks,1997,8(3):532-548.
[8] GERSTNER W,KISTLER W.Spiking neuron models:single neurons,populations,plasticity[M].Cambridge:Cambridge University Press,2002:116-117.
[9] SONG S,MILLER K D,ABBOTT L F.Competitive Hebbian learning through spike-timing-dependent synaptic plasticity[J].Nature Neuroscience,2000(3):919-926.
[10] DAN Y,POO M.Spike timing-dependent plasticity of neural circuits[J].Neuron,2004,44(1):23-30.
[11] 赫建国,倪德克,郑燕.基于Nios Ⅱ内核的FPGA电路系统设计[M].北京:电子工业出版社,2010:3-5.
(责任编辑:石绍庆)
Method for hardware implementation of spiking neural network based on Nios Ⅱ
ZHANG Wen-juan,WANG Lei,WANG Lian-ming
(School of Physics,Northeast Normal University,Changchun 130024,China)
Spiking neural network theory and algorithm are applied to fitting function in this paper,and spiking neural network model is founded based on Nios Ⅱ software using Cyclone Ⅱ EP2C35F672C8N and basic peripheral circuit.Exponential function is fitted and the stabilization error after training is 0.2.The results show that hard implementation of spiking network based on Nios Ⅱ which can provide an effective simulation platform for the research of artificial neural network is successful.At the same time this method can simulate the continuous function effectively and expands the application fields of the neural network.
spiking neural network;hardware implementation;Nios Ⅱ;fitting curve
1000-1832(2016)04-0057-06
10.16163/j.cnki.22-1123/n.2016.04.013
2016-07-21
吉林省科技应用基础研究项目(20130102028JC);中央高校基本科研业务费专项资金资助项目(2412015KJ006).
张文娟(1983—),女,博士,工程师,主要从事嵌入式系统、智能信息处理研究;通信作者:王连明(1972—),男,博士,教授,主要从事嵌入式系统、智能信息处理研究.
TP 183 [学科代码] 520·20
A

