基于BELBIC和FNN的球磨机解耦控制研究

杨国亮，钱 亮，朱松伟

(江西理工大学电气工程与自动化学院，江西 赣州 341000)

基于BELBIC和FNN的球磨机解耦控制研究

杨国亮，钱 亮，朱松伟

(江西理工大学电气工程与自动化学院，江西 赣州 341000)

针对球磨机系统控制过程中存在的多变量、强耦合、模型时变性的特点，提出了基于大脑情感智能控制器(BELBIC)和模糊神经网络(FNN)解耦的复合控制方案.利用模糊神经网络的自适应学习能力设计了球磨机系统解耦器，有效地消除了球磨机系统耦合现象，在此基础上，设计了大脑情感学习智能控制模型.仿真实验表明，本文提出的控制方案优于传统的解耦控制方法，能较好地解决球磨机强耦合问题，且具有较好的鲁棒性.

大脑情感学习智能控制；球磨机；模糊神经网络；解耦控制

0 引言

钢球磨煤机是火电厂等用煤企业常用的大型辅助设备，其耗电量大且是一个非线性、大滞后、大惯性、强耦合和具有多种不确定性扰动的多变量对象，难以使用常规的控制方法实现其自动控制.若长时间采用人工经验的方法、手动调整相关变量的方法控制球磨机系统的运行，则容易出现钢筒内载煤量异常、原煤煤粉泄漏和钢筒出入口温度超标等事故.并且不能够使球磨机处于最佳状态下运行，致使球磨机电能消耗大大增加，造成不必要的经济损失.

1995年Harry Nyquest提出了逆奈奎斯特阵列法，文献[1]将此法用于球磨机控制系统中是把轴瓦振动的垂直分量表征磨煤机内存煤量，这样将给煤回路近似为一个单回路系统，因而可用单变量的方法设计，对磨煤机出口温度和入口负压进行解耦设计，用热风门控制出口温度、由温风控制入口负压.Takagi和Surgeons提出基于标准模型的模糊神经网络，文献[2]将模糊神经网络在应用与球磨机的控制上也有很大的成效，能够适应球磨机的运行工况的变化而引起的动态特性的变化，因为神经网络具备强大的学习能力及对外界环境优秀的适应能力，并且能够对非线性函数进行逼近且不依赖准确的数学模型.所以神经网络控制能够在球磨机的控制中起到一定的作用和效果.

1 大脑情感学习智能控制模型

大脑情感学习模型(BEL)是在模拟了杏仁体和眶额皮质的情感信息交互方式的基础上建立的[3]，主要分为杏仁核和眶额皮质两大主要组成部分.杏仁体是大脑对于情感进行加工记忆处理的重要部位，而眶额皮质重要部分主要处理来自丘脑的刺激，负责加工感官皮层和杏仁核提供的刺激.对每一组情感信号，BEL模型内部都会设立相对应的节点来处理.感官输入信号SI(Sensory Input)作为BEL模型输入信号是由感官输入函数计算得出，而另一则奖励(Reward)输入信号由情感暗示函数计算得出.杏仁体的输入信号主要来自感官输入信号SI、奖励信号REW以及来自丘脑(Thalamus)的信号Ath，眶额皮质所接收的刺激信号主要是感官皮质输入信号SI和来自杏仁体的信号，而不会受到丘脑的信号刺激，BEL模型结构如图1所示[3-4].

图1 BEL大脑情感学习模型

(1)

杏仁体的输出值Ai和眶额皮质的输出值Oi分别为：

Ai=SIi·Vi，i=1，2，…，m，

Am+1=Ath·Vm+1；

(2)

Oi=SIi·Wi，i=1，2，…，m.

(3)

其中：Vi是对应节点Ai的权值，Wi是对应节点Oi的权值.

同时BEL模型以特殊的仿生学权值学习调整杏仁体和眶额皮质的连接权值，具体公式为：

(4)

(5)

其中：λv和λw分别为杏仁体和眶额皮质内的学习率；E′为不受丘脑组织刺激信号时的杏仁体部分的BEL模型输出，表示为

(6)

由(4)式和(5)式可以看出，杏仁体内的权值调节律ΔVi的正负始终与SIi保持一致，说明杏仁体内的情感刺激信号只要经过学习之后，将被永久记忆、状态始终被保持.然后眶额皮质内的权值调节步长ΔWi可取正负，表明眶额皮质在学习过程中起到了对杏仁体抑制和修正的功能，通过奖励信号REW的指引作用减小了误差，指引杏仁体向所预定的期望值进行学习[3].BEL模型的输出为

(7)

C.Lucas等人于2004年将大脑情感学习模型引入智能控制领域[4]，提出了基于大脑情感学习模型的智能控制器(Brain Emotional Learning Based Intelligent Controller，BELBIC).基于BELBIC已经被证明具有较强的鲁棒性，并且能够应用在多输入、多输出系统中，还具备简单、快速响应和得到比较良好的控制品质的特点[4].使用BELBIC作为控制器的控制系统结构如图2所示.图中：y为系统的输出；r为系统的输入；REW为大脑情感学习智能控制器的情感奖励输入；SI为情感输入；u为大脑情感学习智能控制器的输出；e为系统控制误差.

图2 基于BELBIC的控制系统结构示意图

奖励信号REW可以设置为关于BEL模型输出E、系统误差e和系统输出y的函数，表示为

REW=J(e，E，y).

(8)

同时感官输入信号通过情感输入函数得出，一般设置为关于系统输入r、系统输出y、系统控制误差e的函数，即

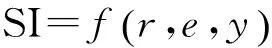
(9)

为了简单起见，本文选择REW和SI信号为：

(10)

(11)

其中k1，k2，k3，k4，k5和k6为常数，可以事先设定.

2 基于BELBIC和模糊神经网络的球磨机控制解耦系统设计

为了最大限度消除球磨机系统耦合现象，本文先利用模糊神经网络(FNN)设计了球磨机控制系统解耦环节，然后设计了BELBIC球磨机控制器，系统结构如图3所示.图中：RM1和RM2为系统参考模型，t和p分别为球磨机出口温度和入口负压.在此解耦模型中每个FNN解耦器都是单输出的，它只负责一个通道的解耦，因此它的结构比较简单，另外，它的指标函数也非常简单，因为总的目标函数已经被分解为单一的目标函数，而且不必再考虑解耦器本身各通道之间的交连问题[6-7].因此，采用分散解耦可以实现对多变量非线性系统的解耦.如图3所示，球磨机控制系统只需要2个解耦补偿器N1，2和N2，1，从而更加简单的解决了强耦合的问题.

图3 BELBIC和FNN的球磨机控制解耦模型

以FNN模型为例，来推导其用于解耦的具体算法.图4为解耦器N1，2的结构图.图中：k1，k2为解耦器N1，2的输入及其变化率的量化因子；k3为比例因子，图中线框内为FNN.

图4 FNN解耦器N1，2的结构

根据上面的分析和FNN的特点可以得到FNN输入层神经元数为2，输出层神经元数为1.设每个输入变量均被分为5个模糊子集，则第2层模糊层有10个节点，第3层的初始节点数为25个，第4层规则合并层的初始节点也为25个.

以FNN中N1，2和N2，1为例，根据FNN的运算过程并结合解耦过程可以得到：

因此有：

(12)

(13)

FNN中的规则数以及隶属度函数中心(宽度)、权值等可通过梯度下降法或GA进行优化[8].整理以上推导的结果，可以得出求分散式FNN解耦器的步骤：

(1) 将FNN解耦器与球磨机出口温度t和入口负压p(被控对象)串联；

(2) 去掉球磨机解耦系统的反馈和BELBIC控制器，使系统处于开环状态；

(3) 设定FNN解耦器规则数及参数的初始值；

(4) 将球磨机出口温度作为系统输入且加入阶跃响应信号，其他通道的输入为0；

(5) 通过遗传算法优化获得通道1对于通道2的FNN解耦器的规则数及参数值，构建FNN解耦器N1，2，使通道2球磨机入口负压p输出y2等于期望输出Y2；

(6) 将通道2的输入加入球磨机入口负压p作为阶跃响应信号，通道1的输入为0；

(7) 仿照(5)通过遗传算法优化获得通道2对于通道1的FNN解耦器的规则数及参数值，构建出FNN解耦器N2，1.

本文设计控制方案具体计算步骤如下：

(1) 设定BELBIC模型参数，并对其权值进行初始化；

(2) 根据(7)式计算BELBIC输出；

(3) 计算解耦环节FNN输出；

(4) 计算参考模型与球磨机系统模型输出；

(5) 根据(4)和(5)式更新BELBIC权值；

(6) 重复(2)—(5)直至设定时间为止.

3 结果与分析

为了验证基于大脑情感学习和模糊神经网络的球磨机解耦控制系统的有效性，为了便于比较，同时采用了PID和FNN相结合的控制方案并进行了仿真实验(文中简称PID+FNN解耦控制).利用文献[5]给出的球磨机模型得到相应的传递函数进行仿真.

球磨机系统数学模型为

图5可以看出模糊神经网络(FNN)解耦控制器大大削弱了球磨机出口温度t和入口负压p2个回路之间的相互影响，在此基础上，可近似将双输入双输出的球磨机系统等同于2个简单单闭环系统.

图5 球磨机系统解耦响应曲线

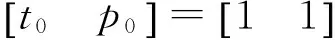
在图6中，y1代表球磨机出口温度，y2代表球磨机入口负压.由2个图对比可知BELBIC+FNN的解耦控制方法的超调量、调节时间明显优于PID+FNN解耦控制方案.

为测试本文设计球磨机控制系统抗干扰性，在球磨机控制系统趋于稳定(500 s)后，在系统内加入幅值为0.1的单位冲激扰动信号，响应曲线如图7所示.由图7可以看出，基于BEL模型的控制方法在有干扰的情况下相比于PID控制器能够较快地恢复稳定并且无震荡.

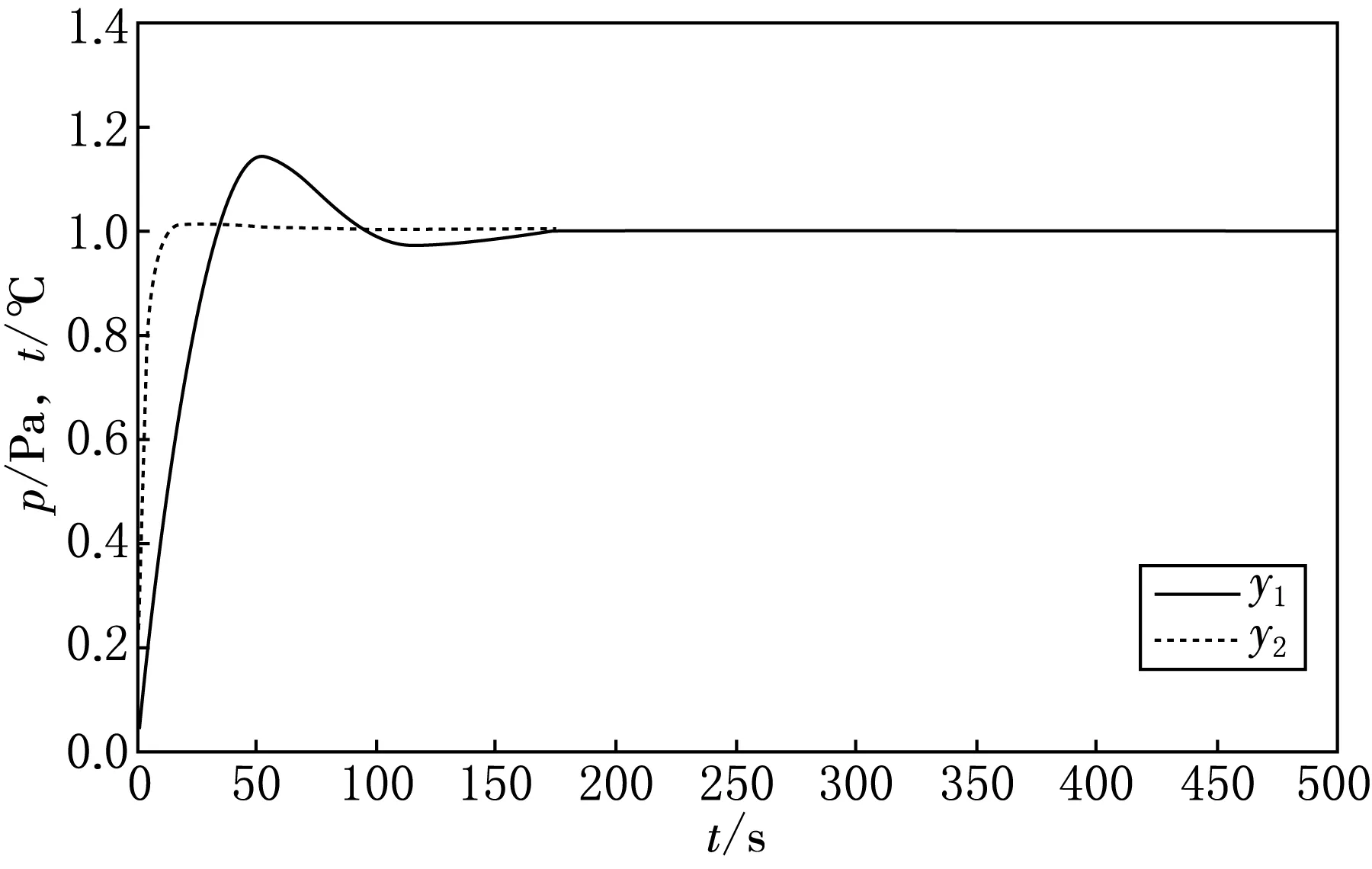
(a)PID+FNN解耦控制 (b)BELBIC+FNN解耦控制

图6 球磨机控制阶跃响应曲线

图7 单位脉冲干扰信号下的响应曲线

4 结论

在传统球磨机系统控制过程中存在的多变量、强耦合的特点，本文引入了基于大脑情感学习模型，构建了大脑情感学习控制器，该控制方法具有简单、响应速度快、抗干扰能力强等特点，并且优于其他传统类型的控制器，同时加入模糊神经网络(FNN)更好的解决了球磨机控制变量存在的强耦合的问题.

[1] 程启明，程尹曼，汪明媚，等.球磨机混合优化前向神经网络PID解耦控制系统[J].电力系统及其自动化学报，2010(2)：54-59.

[2] 吴杰康，陈明华，陈国通.基于PSO的模糊神经网络短期负荷预测[J].电力系统及其自动化学报，2010(2)：54-59.

[3] 王帅夫，刘景林.基于大脑情感学习模型的步进电机控制系统[J].吉林大学学报(工学版)，2014(3)：765-770.

[4] LUCAS C，SHAHMIRZADI D，SHEIKHOLESLAMI N.Introducing BELBIC：brain emotional learning based intelligent controller[J].Intelligent Automation & Soft Computing，2004，10(1)：11-21.

[5] 杨国亮，余佳伟，鲁海荣.情感智能的球磨机系统内模控制研究[J].2015(9)：1071-1074.

[6] 刘长良，梁伟平，李长青.火电厂球磨机制粉系统的自调整模糊控制[J].中国电机工程学报，2001(12)：93-96.

[7] 吴杰康，陈明华，陈国通.基于PSO的模糊神经网络短期负荷预测[J].电力系统及其自动化学报，2007(1)：63-67.

[8] 白江斌，金慰刚，张建华.电厂球磨机的模糊神经网络控制[J].仪器仪表用户，2007，14(1)：43-45.

(责任编辑：石绍庆)

BELBIC and FNN for ball mill decoupling control system research

YANG Guo-liang， QIAN Liang，ZHU Song-wei

(School of Electrical Engineering and Automation，Jiangxi University of Science and Technology，Ganzhou 341000，China)

In view of the multi variable，strong coupling and time-varying characteristics of the ball mill system，a compound control scheme based on brain emotional learning intelligent controller (BELBIC) and fuzzy neural network (FNN) is proposed.Using the adaptive learning ability of the fuzzy neural network，the decoupling device of the ball mill is designed，which effectively eliminates the coupling phenomenon.Through the simulation experiments，the control scheme proposed in this paper is better than the traditional decoupling control method，which can solve the problem of strong coupling of ball mill and has good robustness.

brain emotional learning based intelligent controller；ball mill system；fuzzy neural network；decoupling control

1000-1832(2016)04-0078-05

10.16163/j.cnki.22-1123/n.2016.04.017

2015-11-25

国家自然科学基金资助项目(51365017，61305019)；江西省青年科学基金资助项目(20132bab211032).

杨国亮(1973—)，男，博士，教授，主要从事智能控制、模式识别与图像处理研究；通信作者：钱亮(1990—)，男，硕士，主要从事智能控制研究.

TP 273 [学科代码] 510·80

A