4等周边连通图的邻域条件

徐子钧,张 磊

(晋中学院 数学学院,山西 晋中 030600)



4等周边连通图的邻域条件

徐子钧,张 磊

(晋中学院 数学学院,山西 晋中 030600)

互连网络;γk-最优图;k等周边连通度;邻域

0 引言

本文所考虑的图都是无向简单图.本文中出现而未定义的概念和记号参见文[1].设G=(V(G),E(G))是连通图,用ν(G)=|V(G)|表示G的阶.若e=uv是一条边,则称u和v相邻.G中所有与顶点u相邻的点所组成的集合N(u)叫做u的邻域.假设U是V(G)的一个非空子集.以U为顶点集,以G中两个端点均在U中的所有的边的集合为边集所组成的子图称为G的由U导出的子图,记为G[U];这时,也称G[U]为G的导出子图.导出子图G[V(G)U]记为G-U;它是从G中删去U中的顶点以及与U中的顶点相关联的边后所得到的子图.若U={u},则G-U简记为G-u.图G中的一条途径是指一个有限非空序列W=v0e1v1e2v2…vk-1ekvk,它的项交替地为顶点和边,使得对1≤i≤k,ei=vi-1vi.称W是从v0到vk的一条途径.v0和vk分别称为W的起点和终点.W中边的数目称为W的长.若W的内部的顶点不相交,则称W是从v0到vk的一条k-路.对G的两个非空顶点子集X与Y,用[X,Y]表示G中一端点在X中另一端点在Y中的所有边所组成的集合.

多处理机的互连网络拓扑常以图为数学模型.边连通度是一个传统的度量网络的可靠性参数.作为边连通度的推广,Fbrega和Fiol[2]提出了k限制边连通度,记为λk(G).从最近关于k限制边连通度的研究结果来看[3-6],λk(G)越大,网络越可靠.作为k限制边连通度的一种推广,k等周边连通度的概念由Hamidoune等人[7]在2000年提出.

定义1 设k是一个正整数,G是一个阶ν(G)≥2k的图.G的k等周边连通度定义为:

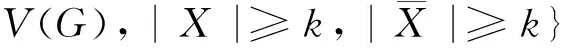
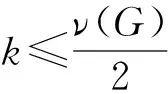
令

⊆V(G),|X|=k}.

显然,γk(G)≤βk(G).2007年,张昭和原晋江[8]给出了γk-最优图的定义.

定义2 设k是一个正整数,G是一个阶ν(G)≥2k的连通图.如果γk(G)=βk(G),那么称G是γk-最优的.

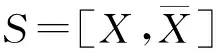
2009年,王世英等人[9]给出了一个图是γk-最优的邻域条件.

定理1[9]设k是一个正整数,G是一个阶ν(G)≥2k的图.如果对G中任意两个不相邻顶点u,v都有

那么G是γk-最优的.

本文将给出γ4-最优图的邻域条件,这个结果在k=4时,改进了定理1.

1 主要结论

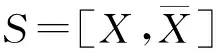
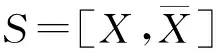
i)如果在X中存在一个基数为k的子集U使得

那么G是γk-最优的.

ii)X中不存在基数为k的子集U使得

定理2 设G是一个阶ν(G)≥8的图.如果对于G中任意一对不相邻的顶点u,v,当u和v都不在三角形中时满足

当u和v中至少有一个在三角形中时满足

那么G是γ4-最优的.

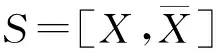
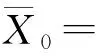
(1)

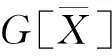
且

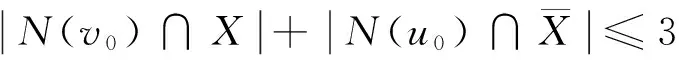
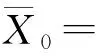
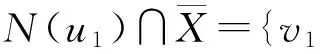
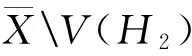
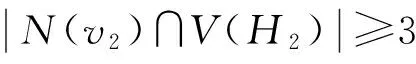
(2)

根据断言1和断言2,我们得知对于任意的u∈X有

由引理1(i)知,G是γ4-最优的,矛盾.因此XV(H4)中至少存在一点u2使得

进一步,我们有

由引理1(i)知,G是γ4-最优的,矛盾.

综上所述,G是γ4-最优的,矛盾.

由定理2,我们容易得到下面的结论.

推论1设G是一个阶ν(G)≥8的无三角形图.如果对于G中任意一对不相邻的顶点u,v都有

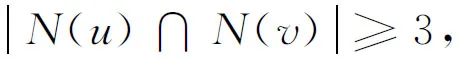
那么G是γ4-最优的.

[1] BONDY J A,MURTY U S R.Graph Theory[M].New York:Springer,2008

[3] WANG Ming,LI Qiao.Conditional edge connectivity properties,reliability comparisons and transitivity of graphs[J].Discrete Mathematics,2002,258(1-3):205-214

[4] LI Qiaoliang,LI Qiao.Reliability analysis of circulant graphs[J].Networks,1998,31(2):61-65

[5] XU Junming,XU Keli.On restricted edge-connectivity of graphs[J].Discrete Mathematics,2002,243(1-3):291-298

[6] BOESCH F T.On unreliability polynomials and graph connectivity in reliable network synthesis[J].Journal of Graph Theory,1986,10(3):339-352

[7] HAMIDOUNE Y O,LLADA S,SERRA O,et al.On isoperimetric connectivity in vertex-transitive graphs[J].SIAM Journal on Discrete Mathematics,2000,13(1):139-144

[8] ZHANG Zhao,YUAN Jinjiang.Degree conditions for restricted-edge-connectivity and isoperimetric-edge-connectivity to be optimal[J].Discrete Mathematics,2007,307(2):293-298

[9] WANG Shiying,LIN Shangwei,LI Chunfang.Sufficient conditions for super k-restricted edge connectivity in graphs of diameter 2[J].Discrete Mathematics,2009,309(9):908-919

Neighborhood Conditions for 4-Isoperimetric Edge Connected Graphs

XU Zijun, ZHANG Lei

(School of Mathematics, Jinzhong University, Jinzhong 030600, China)

interconnection networks;γk-optimal graph;k-isoperimetric edge connectivity; neighborhood

2016-01-06

徐子钧(1987-),女,山西临汾人,硕士,晋中学院数学学院助教,主要从事图论及其应用研究.

1672-2027(2016)02-0019-04

A