空气中PM2.5演变规律的研究
——以合肥市为例
李东玲,杨鹏辉,胡 颖,袁则奕
(1.安徽财经大学 金融学院,安徽 蚌埠 233030;2.安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
空气中PM2.5演变规律的研究
——以合肥市为例
李东玲1,杨鹏辉2,胡 颖2,袁则奕1
(1.安徽财经大学 金融学院,安徽 蚌埠 233030;2.安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
针对空气中PM2.5的演变规律问题,运用SPSS定量分析PM2.5浓度和气温、风力、湿度等气象因素与季节因素的相关系数,定性分析PM2.5浓度在气温、风力、湿度等气象因素与季节因素影响下的变化特征,结合传统的大气点源高斯扩散及其法定推荐修正模型,逐步改进,建立多因素影响下的多元高斯扩散模型,并通过残差检验模型的合理性.
PM2.5演变规律;定性分析;定量分析;多元高斯扩散模型;合肥市
空气质量问题始终是人们关注的热点问题.近年来,我国大范围持续的雾霾天气严重危害人民的健康,而产生雾霾的主要因素是一种大气中直径小于或等于2.5 μm的颗粒物——PM2.5.PM2.5的主要来源包括“自然源”和“人为源”,分为一次颗粒物和二次颗粒物,其形成过程比较复杂,成分主要由水溶性离子、颗粒有机物和微量元素等组成.目前已有不少文章探究导致PM2.5产生的因素,却少有文章探讨PM2.5的演变规律,本文以合肥市2014年4月1日到2015年6月30日的天气数据为例,以传统的大气点源高斯扩散及其法定推荐修正模型[1-2]为基础,综合考虑气温、温度、风力等气象因素和季节因素的影响,建立多元高斯扩散模型,得出合肥市PM2.5的分布规律,为环保部门减轻其危害和制订防治策略提供理论依据.
1 数据来源与模型假设
从合肥市空气质量监测网站[3]搜集数据,主要数据是合肥市从2014年4月1日到2015年6月30日的历史天气数据和合肥市PM2.5监测点——蜀山区2015年7月的历史天气数据,采用灰色预测法对数据中的缺失值进行补充,剔除明显异常值,保证数据整体上的连续性与准确性.PM2.5的演变规律比较复杂,现做出如下假设:1)风向水平,风速风向恒定;2)PM2.5在平整、无障碍物的地面上扩散;3)扩散过程中浓度在轴上的变化分布是高斯分布;4)地标及地标物对PM2.5没有吸收;5)物质衰减系数相同.
2 空气中PM2.5的演变规律
2.1 研究思路
为探究PM2.5浓度在气温、风力、湿度等气象因素与季节因素影响下的演变规律,我们搜集合肥市历史天气数据,依次定量分析PM2.5浓度在气温、风力、湿度等气象因素与季节因素的相关关系,并结合定性分析得出气温、风力、湿度等气象因素与季节因素对PM2.5演变规律的影响,逐步对模型做出改进,利用合肥市PM2.5监测点——蜀山区的历史天气数据对模型进行检验,得出空气中PM2.5的演变规律.
2.2 高斯扩散模型
为使研究简单明了,我们假设PM2.5的排放为点排放,不考虑燃料燃烧、汽车尾气等普遍排放的影响,当然点污染源可以推广到线污染源、面污染源等,即将两个污染源的PM2.5浓度叠加得到线污染源、将多个污染源的PM2.5浓度叠加得到面污染源,因而具有推广性.我们选择传统的大气点源高斯扩散及其法定推荐修正模型,PM2.5在扩散过程中,以风向为X轴正半轴,风速用μ表示,水平垂直方向为Y轴,垂直于XOY平面为Z轴,有效高度用He表示,O为原点,即PM2.5排放点,其强度用Q表示,浓度用C表示.
其中,σy为高斯空气污染扩散模型水平扩散参数,σz为高斯空气污染扩散模型垂直扩散参数.
2.3 模型改进及简化
PM2.5的演变会受到气温、温度、风力等气象因素和季节因素的影响,依据整理好的合肥市从2014年4月1日到2015年6月30日的历史天气数据,依次分析气温、风力、湿度等气象因素和季节因素对PM2.5的影响,进而对模型进行改进.
2.3.1 温度作用下的高斯扩散模型
运用EXCEL做出PM2.5与气温的折线图.
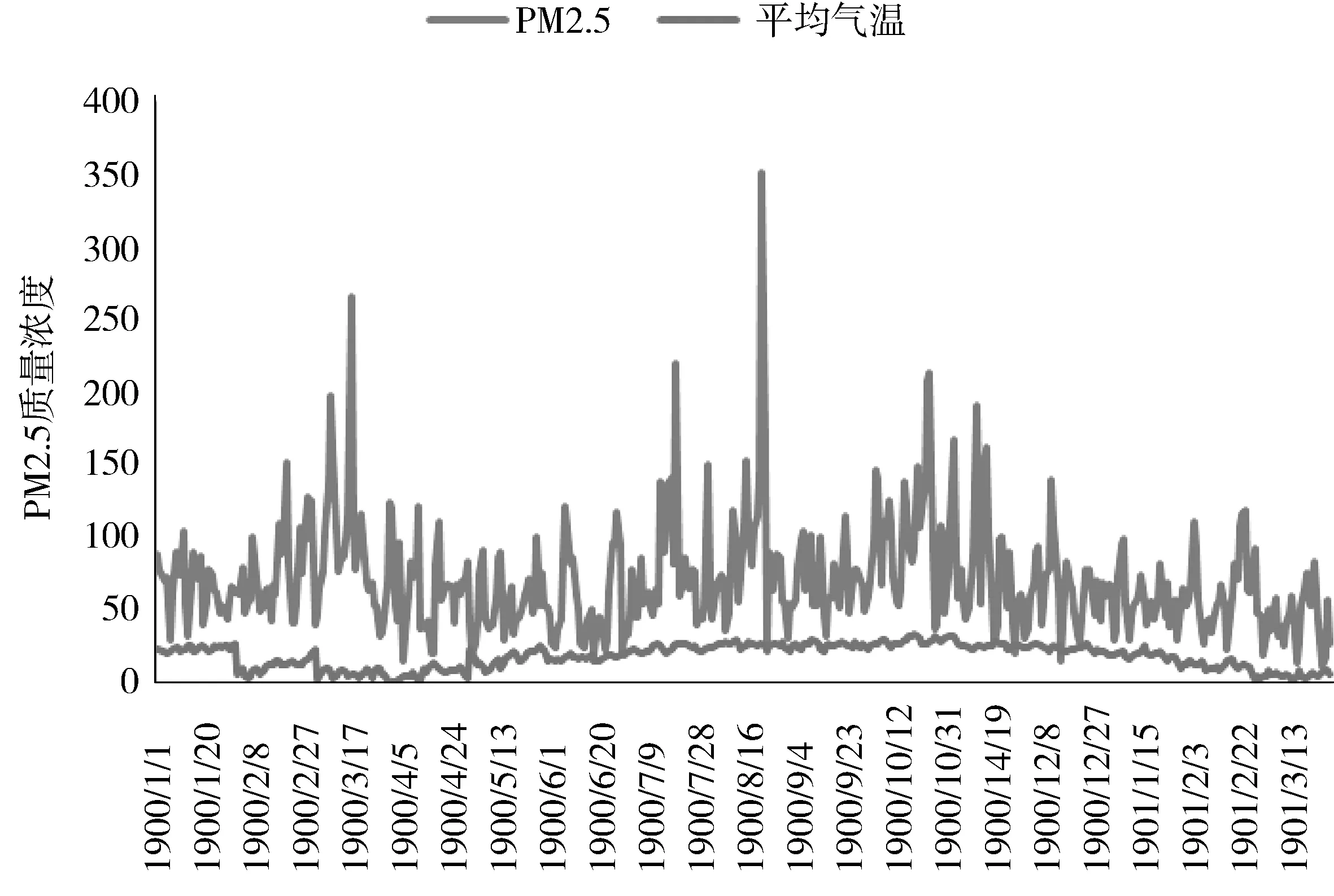
图1 PM2.5与气温的折线图
由图1可以看出,PM2.5日平均质量浓度和日平均气温的关系并不明显[4],在平均气温波动很大的情况下,PM2.5质量浓度只有小幅度波动,而在平均气温波动很小,几乎没有波动的情况下,PM2.5质量浓度却呈现大幅度波动.因此气温的变化基本不对PM2.5浓度产生影响,PM2.5的高斯扩散模型不作改进.
2.3.2 风力作用下的源衰减模型
运用SPSS对数据进行分析得出PM2.5与风力的关系.
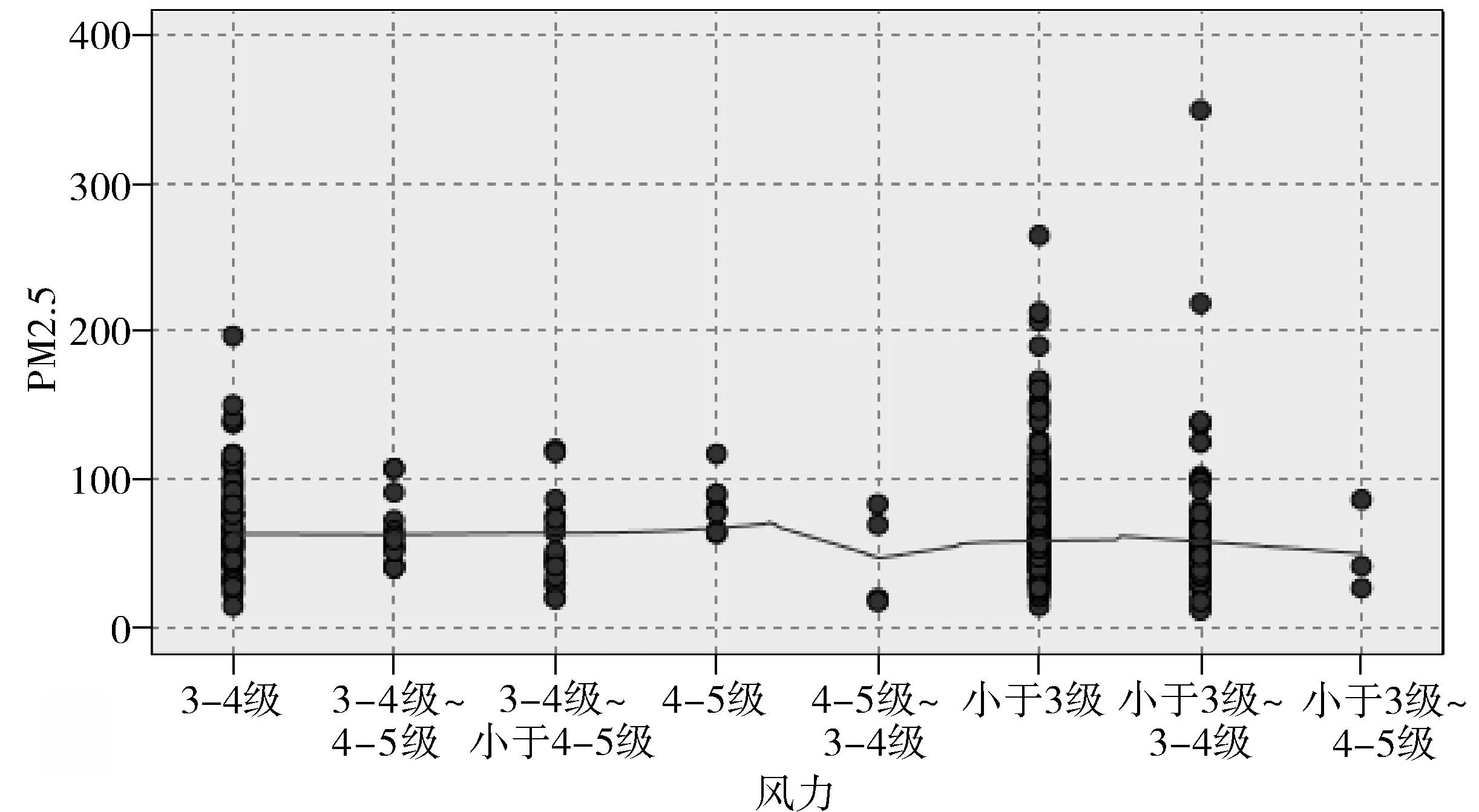
图2 PM2.5与风力散点关系图
图2中SPSS局部拟合出的多条回归线显示,风力越大,PM2.5质量浓度越低,这是因为风速越大, 大气湍流强度越大, 对污染物扩散稀释的能力越强, 导致 PM2.5质量浓度下降;反之则浓度上升,因此大气污染物在风力作用下不断扩散稀释的过程中连续不断地从大气向地表作质量转移,从而减少了其在空气中的浓度,我们对高斯扩散模型进行改进得到源衰减模型:
此外,我们可以看到在风力一样的情况下, PM2.5质量浓度也有较大的变化, 说明PM2.5质量浓度还受到其他气象因素的影响,因此对PM2.5的演变规律作进一步的探讨.
2.3.3 湿度作用下的湿沉积模型
不同的天气,湿度也不相同,一般而言阴雨天气湿度相对较高,运用SPSS进行分析得出PM2.5与湿度关系.
图3 PM2.5与湿度散点关系图
图3中SPSS局部拟合出的多条回归线显示,两者呈现正相关,这主要是因为湿度越大,越有利于大气中的气体物质转化成为二次粒子,且一些极细的颗粒由于吸湿使本身含液量增加,粒子涨大从爱根核模态转化为积聚核模态, 造成空气中PM2.5的质量浓度增加.考虑湿度对大气污染物源强的影响,我们对源衰减模式进行改进得到湿沉积模式:
同时我们看到在湿度一样的情况下, PM2.5质量浓度也有较大的变化, 说明PM2.5质量浓度还受到其他因素的影响,见表1.
2.3.4 季节变迁模型
季节变迁模型见表1所示.

表1 PM2.5的季节平均浓度
运用EXCEL做出PM2.5与季节的柱状关系图,见图4.

图4 PM2.5与季节的柱状关系图
由图4我们可以看到,春季PM2.5的质量浓度最高,其余三个季节PM2.5的质量浓度相近.春季 PM2.5的质量浓度最高主要由频繁发生的沙尘天气[4]引起,除此之外, 春季气候干燥, 少雨多风从而具备扬尘条件也是一个原因.考虑大气污染物PM2.5在季节作用下不断变迁,我们对湿沉积模型进行改进得到季节变迁模型:
不难发现源衰减模型、湿沉积模型及季节迁移模型三者表达式形式基本一致性,将其综合起来简化为:
Qx=Q0exp(-f(x))
f(x)=β1x1(m)+β2x2(m)+β3x3(m)+β4x4(m)+ε
其中,自变量为x1(m)湿度,x2(m)为气温,x3(m)为风力,x4(m)为季节,β1,β2,β3,β4为其相应与PM2.5的相关性系数[5].ε为随机误差[6]且服从于正态分布.
已假设各个地区衰减系数相同,所以可以将衰减项进一步简化,即:
多元高斯扩散模型表示为:
其中C0表示前一天的污染物浓度,
Qx=Q0exp(-f(x))
f(x)=β1x1(m)+β2x2(m)+β3x3(m)+β4x4(m)+ε.
3 结果分析与模型检验
对合肥市蜀山区2015年7月的历史数据进行处理,为便于计算我们将天气按照从晴天、多云、阴、小雨、大雨、雷阵雨、暴雨、雪依次编号为0,1,2,3,4,5,6,7,同理风力按照小于3级,3~4级,4~5级依次编号为1,2,3,季节按照春、夏、秋、冬依次编号为1,2,3,4,这样得到新的监测点的历史天气数据.
运用SPSS的相关性分析得出PM2.5与气温、湿度、风力、季节的相关性系数依次为0.178,0.107,-0.026,0.201,源衰减系数k取0.000 01,经测得:源强Q为235.6,前一天的浓度C为26 μg/m3,平均风速为5 m/s,运用MATLAB分别对监测点——蜀山区的数据进行运算得到相应的PM2.5数值;以及蜀山区PM2.5扩散曲面图;PM2.5浓度等值曲线局部放大图.

图5 PM2.5浓度等值曲线局部放大图

图6 PM2.5扩散曲面图
由图5、图6可以看出,PM2.5的扩散速度随距离的增大先变快,后变慢,逐渐接近于0.
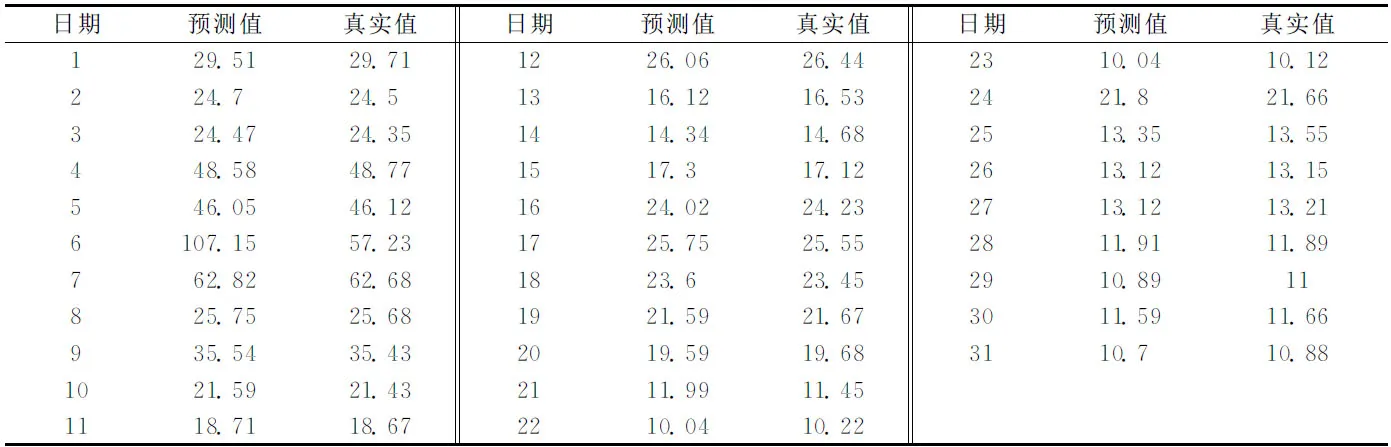
表2 蜀山区2015年7月预测值与真实值对比表
从表2中可以看出,监测点的PM2.5的计算值与真实值并没有太大区别,为保证模型和方法的合理性,我们通过残差分析来判读计算出的数据是否正确、合理,考虑到统计数据时出现的误差,为排除误差的影响,我们以31天的平均残差为标准,表中蜀山区7月6号的数据可能是由于受到其他方面影响,相差较大,为了使结果更加正确,剔除7月6号的数据.运用EXCEL得到,蜀山区的平均残差为0.165<0.2,因此可以判断模型合理.
4 结语
本文根据合肥市2014年4月1日到2015年6月30日的数据展示出气温、风力、湿度等气象因素与季节因素与PM2.5的浓度之间的关系,结合高斯扩散模型建立多元高斯扩散模型,并利用残差检验出模型合理.
此外,本模型不仅适合分析合肥市PM2.5的演变规律,也适合其他地区,例如北京、上海等地区,也可以用来探索其他污染气体和小颗粒的成因和演变规律.
[1] 何国玺,冯 浩,张浩然.空气中PM2.5的扩散和衰减模型[J].数学的实践与认识,2014,44(15):29-30
[2] 李海燕,李 治,胡曹园,等.空气中的扩散衰减与预测分析[J].数学的实践与认识,2014,44(15):67-70
[3] 天气网.合肥市历史天气数据[DB/OL].链接:http://lishi.tianqi.com/hefei/index.html,2014-04-01
[4] 刘随心,曹军骥,安芷生.西安大气细粒子(PM2.5)质量浓度变化特征及其影响因素[J].过程工程学报,2009(2):232-234
[5] 蒋雪峰,李 洁,蒋 奎,等.空气中PM2.5问题的建模研究[J].数学的实践与认识,2014,44(15):51-52
[6] 陈 媛,岑 况,NORRA S,et al.北京市区大气气溶胶PM2.5污染特征及颗粒物溯源与追踪分析[J].现代地质,2010(2):347-350
Study on the Evolution of PM2.5 in the Air——For Example as Hefei
LI Dongling1, YANG Penghui2, HUYing2, YUAN Zeyi1
(1.Anhui Finance and Economics University, School of Finance, Bengbu 233030; 2.Anhui University of Finance and Economics Institute of Statistics and Applied Mathematics, Bengbu 233030, China)
In the light of the evolution law of PM2.5 in air, the variation characteristics of PM2.5 concentration in air temperature, wind, humidity and other meteorological factors were analyzed. The correlation coefficient between PM2.5 concentration and temperature, wind, humidity and other meteorological factors was analyzed by SPSS, based on the traditional atmospheric point source Gauss diffusion and its legal recommendation model, the model of multivariate Gauss diffusion is established, and the rationality of the model is tested by residual error.
PM2.5 evolution law; qualitative analysis; quantitative analysis; multivariate Gauss diffusion model; Hefei City
2016-01-23
国家自然科学基金(11301001),国家级大学生创新项目(201510378020).
李东玲(1994-),女,河南信阳人,安徽财经大学金融学院在读硕士研究生,主要从事金融数学研究.
1672-2027(2016)02-0068-05
X823
A

