图中包含4-圈和6-圈的[1,2]-因子

鲁富荣

(山西大学 商务学院 基础教学部,山西 太原 030031)



图中包含4-圈和6-圈的[1,2]-因子

鲁富荣

(山西大学 商务学院 基础教学部,山西 太原 030031)

设k为一个正整数,图G是一个顶点数为4k的简单图,当δ(G)≥2k+1时,文章证明了图G包含一个由k-3个4-圈,一个6-圈及一条至少包含三条弦的6-路构成的[1,2]-因子．

[1,2]-因子;最小度;圈

0 引言

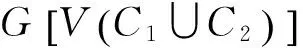
一条边e=uv称之为一条路P的弦,若有{u,v}⊆V(P),e∉E(P)．

1984年Zahar[2]作出了如下猜想:若图G的顶点数为n=n1+n2+…+nk且满足δ(G)≥「n1/2」+「n2/2」+…+「nk/2」,则G包含k个相互独立的长度分别为n1,n2,…,nk的圈.

在此基础上Erdos and Faudree[3]猜想如果图G是一个顶点数为4k的图,且δ(G)≥2k,则图G包含k个顶点不相交的4-圈．H.Wang在2010年给出了上述猜想的证明．

定理[3]|G|=4k.如果δ(G)≥2k,则G包含k个相互独立的4-圈．

引文[4]进一步给出了下面的结论:

对于满足|G|=4k的图G,如果δ(G)≥2k+4,则G包含k-3个4-圈和2个6-圈,使得这k-1个圈是相互独立的．

本文在上述工作的基础上证明了如下结论:

定理1 对于简单图G, |G|=4k,δ(G)≥2k+1,图G包含k-3个4-圈,一个6-圈及一条至少包含三条弦的6-路(k≥3).

1 引理及其证明

引理1 设图G包含一个4-圈C=x1x2x3x4x1和与之独立的两个顶点x,y,若d(x,C)+d(y,C)≥5,则C∪{x,y}生成的子图中包含一条长为5的含6个顶点的路,且6-路至少包含三条弦．

证明 不妨设d(x,C)≥d(y,C),则有d(x,C)≥3,由对称性,不妨设{x1,x2,x3}⊆N(x,C),因此xx1,xx3∈E(G),又因为d(x,C)≤4,故d(y,C)≥1,若yx4∈E(G)时,则图G包含6-路xx1x2x3x4y,且包含弦xx2,xx3,x1x4．若yx2∈E(G),类似可得结论．若yx1∈E(G)时,则图G包含6-路xx2x3x4x1y,同时图G包含弦xx1,xx3,x1x2．若yx3∈E(G),类似可得结论．

2 定理及其证明

定理1 对于简单图G,|G|=4k,δ(G)≥2k+1,图G包含k-3个4-圈,一个6-圈及一条长为6的路(k≥3).

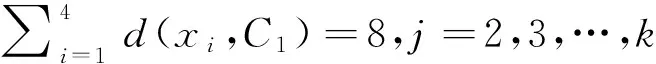
情形1.1 若d(x1,Cj)=2时,对于k=2,3,4,d(xk,Cj)=2时,由对称性,设x1y1∈E(G),此时若有x2y2或x2y4∈E(G),则可得在G[vC1∪Cj)]中存在一个6-圈和与之独立的一条边e,若设e=uυ,H1=G-C1-Cj,则有d(u,H1)+d(v,H1)≥4k+2-14=4(k-3).

当k=3时,设C2=y1y2y3y4y1,C3=z1z2z3z4z1,Cj=C2,且有x1y1或x4y2∈E(G),若e(y3y4,C3)≥1,则可得结论,故我们只需考虑e(y3y4,C3)=0的情形，由于δ(G)≥7,故有d(y3,C1)=d(y4,C1)=4,故由类似讨论可知d(y1,C3)=d(y2,C3)=0,因此e(C1,C3)=12.此时易得结论．

当k>3 时,d(u,H1)+d(v,H1)≥4(k-3)≥4,则在H1中至少存在一个圈C′,使得d(x3,C′)+d(x4,C′)≥1,故有G[VC′∪{x3,x4})]含一条包含6个顶点的路,此时结论成立.

因此,由对称性,若有x4y2或x4y4∈E(G),同理可证结论成立.因此只能有x4y1,x4y3∈E(G),同理有x2y1,x2y3∈E(G),故e(x2,C2)=e(x4,C2)={y1,y3},x4y2,x4y4∉E(G),x2y2,x2y4∉E(G),同理由对称性,由于x4y1,x4y3∈E(G),故e(x1,C2)=e(x3,C2)={y1,y3},故d(x4,H1)+d(y2,H1)≥4k+2-(3+2+3)=4k-6>4(k-2).也即在H1的k-2个4-圈中至少存在一个4-圈C1,使得d(x4,C1)+d(y2,C1)≥5.由引理1,C1∪{x4,y2}生成的子图中包含一条长为5的含6个顶点的路P,且路P至少包含3条弦,结论得证．

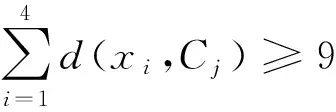
[1] BONDY J R,MURTY U S R. Graph theory with applications[M].Amsterdam:North-Holland,1976

[2] ELZAHAR M H.On circuits in graphs[J].Discrete Math,1984,50:227-230

[3] WANG Hong.On the maximum number of independent cycles in a Bipartite Graph[J]. Journal of Combinatorial Theory, Series B,1996,67,152-164

[4] LU Furong. Disjoint 6-cycles and 4-cycles in graphs[J].Journal of Taiyuan Normal University,2012,4:10-11

A [1,2]-Factor Containing Disjoint 6-Cycles and 4-Cycles in Graph

LU Furong

(Business College of Shanxi University, Taiyuan 030031, China)

Letk≥3 be a positive integer.LetG=(X,Y;E)be a graph with |G|=4k.Supposingδ(G)≥2k+1,then G has a spanning subgraph consisting ofk-3 quadrilaterals, one 6-cycle and a path of order 6 which containing three chords at least such that all of them are independent.

[1,2]-factor;minimal degree; cycle

2016-03-21

山西大学商务学院科研基金项目(2014030).

鲁富荣(1981-),男,山西河曲人,硕士,山西大学商务学院基础教学部讲师，主要从事图论及其应用、复杂网络研究．

1672-2027(2016)02-0012-02

O157.5

A