基于细观有限元方法的复合材料横向力学性能分析
刘万雷,常新龙,张晓军,张 磊
(第二炮兵工程大学,西安 710025)
基于细观有限元方法的复合材料横向力学性能分析
刘万雷,常新龙,张晓军,张 磊
(第二炮兵工程大学,西安 710025)
横向断裂是制约复合材料结构设计的关键点,传统细观模型因为不能充分考虑组分性能、体积分数和纤维形状及分布情况而不能有效预测材料横向力学性能。采用改进的随机序列吸收算法建立具有随机纤维分布的复合材料代表性体积单胞模型,考虑基体破坏和界面脱粘两种失效模式和固化过程中产生的残余应力,对模型在横向拉、压、剪3种载荷下的力学行为进行仿真计算。分析了不同界面强度对复合材料力学性能的影响规律。仿真结果与实验数据对比表明:横向模量预测误差在7%以内,压缩和剪切的强度误差在8%以内,结果一致性较好,表明该模型能够有效预测复合材料横向力学性能。
复合材料;细观有限元;残余应力;界面强度;横向力学性能
复合材料在受到多轴载荷作用时,往往首先出现垂直于纤维方向的横向断裂,这也成为制约复合材料结构设计的重要因素。然而,复合材料横向破坏与其基体和界面性能密切相关,传统的解析方法因不能充分考虑组分性能、体积分数和纤维形状及分布情况[1],在应用时受到很大限制。
随着有限元技术和细观力学的发展使得建立复杂模型分析复合材料失效机理成为可能。Gonzalez等[2]建立了具有随机纤维分布的单向复合材料RVE单胞,采用细观有限元方法预测了复合材料在横向压缩载荷作用下的应力-应变响应曲线,并分析了界面强度对横向压缩性能的影响规律。Vaughan等[3,4]采用实验与数值计算相结合的方法,提出了一种生成高体积分数复合材料RVE单胞的新算法,RVE单胞中纤维之间距离的分布规律与实际细观结构一致性较好。Lu等[5]通过细观有限元方法研究了界面性能对三维编织复合材料单轴拉伸强度的影响,仿真结果与实验数据吻合较好。Yang等[6]利用细观计算力学方法研究了单向复合材料在横向拉伸和压缩时的力学特性,生成了纤维随机分布的RVE单胞,并主要考虑了基体塑性变形和界面脱粘的影响,研究了界面性能对于复合材料损伤特性的影响规律。雷友锋等[7]利用细观有限元方法对三维RVE单胞进行了有效模量的计算,与部分实验结果具有较好的一致性,但其采用的RVE单胞中纤维是均匀分布的,与实际情况出入较大;王兆清等[8]采用重心有限元法对单向纤维复合材料横截面有效弹性模量进行了数值分析,与传统有限元方法相比,该方法计算效率较高;徐强等[9]通过Python语言对ABAQUS进行了二次开发,发展了一种含界面的单向复合材料渐进损伤模型,研究了纤维排列方式及体积含量对材料横向拉伸力学性能的影响。
然而,以往的研究中较少考虑固化过程中残余热应力对复合材料性能的影响,Hojo等[10], Maligno等[11]研究表明残余热应力的存在使得复合材料加载之前就会在界面处出现损伤,因此研究复合材料横向力学性能时有必要将这一因素考虑在内。本工作采用细观有限元方法研究了纤维增强复合材料横向力学性能。建立了具有随机纤维分布的复合材料细观单胞模型,模型中考虑横向加载时基体塑性破坏和界面脱粘两种典型的损伤模式。采用摩尔-库仑塑性模型和Ductile失效准则相结合模拟基体塑性破坏,用Cohesive单元模拟界面脱粘。模型中同时考虑了固化过程中产生的残余应力对复合材料横向力学性能的影响。最后用ABAQUS/Explicit程序对细观单胞模型在横向拉伸、压缩、剪切3种载荷作用下的力学响应进行了仿真计算,采用细观均匀化方法预测了复合材料横向力学性能,并分析了不同界面强度对复合材料横向力学性能的影响规律。
1 复合材料细观力学模型
复合材料横向力学性能主要受基体塑性变形和界面脱粘两方面的影响,本工作将纤维视为横观各向同性的弹性材料,将基体看成是各向同性的弹塑性材料,组分性能如表1所示。用摩尔-库仑塑性模型[12]描述基体的非线性行为,该模型中认为材料屈服发生在剪应力作用的平面,当其达到一个临界值时,发生塑性变形,这个临界值依赖于平面的法向应力,用下式表示:
τ=c-σtanφ
(1)
式中c和φ分别代表黏聚力和摩擦角,这两个常数控制着材料的塑性行为。黏聚力c代表纯剪切情况下材料的屈服应力,摩擦角φ代表静水压力对材料塑性的影响。φ=0时,摩尔-库仑模型退化为Tresca模型,当φ=90°时,演化为Rankine模型。这两个参数都可以通过拉伸和压缩强度获得:
(2)
固体断裂面遵循摩尔-库仑准则,并且单轴压缩时的断裂角度α与摩擦角φ之间的关系如下:
α=45°+φ/2
(3)
典型的环氧基体材料中有50°<α<60°,这样10<φ<30°。一旦φ固定,则对应的c值也就确定了,由文献[13]知基体拉伸和压缩强度分别为80MPa和120MPa,故可以确定摩擦角φ=12°,c=50MPa。假设c和φ为常数,独立于累积塑性应变,摩尔库仑模型的屈服面以最大和最小主应力表示如下:
F(σΙ,σIII)=(σΙ-σIII)+(σΙ+σIII)sinφ-2ccosφ=0
(4)
(5)

表1 玻璃纤维/环氧树脂复合材料组分性能[13]
Table 1 Constituent properties of glass fiber/epoxy resin matrix composite[13]

MaterialE/GPaG/GPaνXt/MPaXc/MPaS/MPaFiber80330.2021501450—Matrix3.351.480.358012075
复合材料横向断裂常常是由于纤维/基体界面脱粘和基体微裂纹等细观损伤积累引起的,这些细观损伤与许多因素有关,其中影响最大的因素是不同组分之间的黏合力。本工作采用一种基于物理机制的零厚度Cohesive界面单元及Traction-Separation本构模拟纤维/基体界面损伤,并认为界面单元的拉伸和剪切强度相等[14]。二维界面单元中存在两个应力分量(tn,ts)和两个位移分量(δn,δs),初始时,界面应力和位移为线性关系,当界面应力达到损伤初始准则后,损伤萌生,界面的应力和位移关系不再保持线性变化,采用二次应力准则作为初始失效准则:
(6)

复合材料横向加载时,法线方向存在受拉和受压两种状态,当受压时,无论是否存在损伤,其压缩刚度保持为初始刚度;当受拉时,其刚度根据损伤程度进行折减(如图1所示,其中K代表界面刚度):
(7)
式中:δn代表法向位移,δ0代表初始损伤位移,δf代表失效位移,δmax代表积分点处计算得到的最大有效位移,d为损伤参数。
采用断裂能准则判断界面最终失效:
(8)
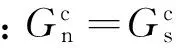

图1 Cohesive单元牵引拉伸失效规律
2 细观有限元模型建立
2.1 RVE单胞生成
本工作采用二维方形RVE单胞计算复合材料横向力学性能。RVE单胞是由随机排列的圆形纤维嵌入在基体中组成的,仿真中一个重要的问题就是确定RVE单胞的尺寸,一方面需要尽量缩小RVE单胞的尺寸减小计算量,同时又需要保证RVE单胞中包含足够的信息能独立代表复合材料性能,由文献[15]可知包含30根纤维的RVE单胞可以满足此条件。
采用改进的随机顺序吸收算法[16](算法如图2所示)生成63μm×63μm的方形RVE单胞,单胞中包含30根随机排列的纤维,纤维直径为5μm,体积分数为60%,误差控制在1%以内。包含30根纤维的RVE单胞如图3所示。

图2 改进随机顺序吸收算法流程图

图3 RVE单胞周期性边界条件施加示意图
2.2 周期性边界条件的施加
含周期性单胞的材料在外载荷作用下,其应力和应变场呈现出连续性和周期性,因此需要对RVE单胞施加周期性边界条件,确保得到合理的细观应力、应变分布。对图3所示的二维单胞施加周期性边界条件[17]的方程如下:
(9)
(10)
对于四个角节点OABC施加如下约束:O点全约束,A,C节点可以根据施加载荷的需要确定施加的约束;B点约束方程为:
uB=uA+uC
(11)
将上述方程用脚本语言python编写成子程序供ABAQUS软件调用,完成对RVE单胞周期性边界条件的施加。
2.3 模型的网格划分及界面单元的建立
采用四边形单元CPE4R单元和三角形单元CPE3对RVE单胞进行网格划分,在基体和纤维边界添加二维Cohesive单元COH2D4,添加Cohesive单元的程序流程如图4所示。

图4 Cohesive单元添加算法
3 横向载荷作用下的力学性能分析
复合材料固化降温过程中由于纤维和基体的热膨胀系数不同,会在纤维/基体界面处产生残余应力,为了让仿真结果更接近实际情况,在计算过程中需要考虑残余应力的影响。纤维和基体的热膨胀系数分别取为15×10-6/K,45×10-6/K,固化温度从175℃降到室温25℃[17]。
通过对RVE单胞施加不同的初始边界条件,可以实现横向拉伸、压缩和剪切加载。计算结束后提取单胞应力、应变,然后采用均匀化方法[1]得到宏观尺度的应力应变响应,计算公式如下:
(12)
通过式(12)可以确定不同载荷下复合材料宏观的应力应变关系,根据应力应变关系可以求出复合材料的横向模量、强度等力学性能参数。
采用ABAQUS/Explicit显示有限元分析软件(可以有效避免数值计算的收敛性问题)对所建立的单胞模型进行拉、压、剪计算(界面强度取值为50MPa,界面刚度为108MPa/m),并将计算结果与文献中实验结果[13]对比,如表2所示。可以看出,仿真计算结果与实验结果较为一致,表明本工作所建的模型适合于复合材料横向力学性能预测。
表2 复合材料横向力学性能预测结果与实验结果[13]对比
Table 2 Comparison between simulation results and experimental results[13]

ResultEt/GPaEc/GPaG/GPaXt/MPaXc/MPaS/MPaSimulation16.5317.175.4638.92122.5076.16Experiment17.7017.705.8335.00114.0072Error6.61%3.00%6.78%11.20%7.46%5.78%
在复合材料加工制作过程中,纤维/基体界面强度会受到多种因素的影响,且可以通过不同实验手段提高界面强度,因此有必要研究不同界面强度对复合材料横向力学性能的影响。本工作对25,50,80MPa(约等于基体拉伸强度)和100MPa四种界面强度下的复合材料横向力学性能变化规律进行了对比分析。
3.1 拉伸载荷
在图3中点A处施加X方向位移载荷,固定点O,限制点C的转动自由度和X方向位移自由度,即可完成拉伸位移的施加。图5中给出了3种不同界面强度下,横向拉伸应力与应变之间的关系,“w/”代表考虑残余应力的影响,“w/o”代表不考虑残余应力影响的情况。从图5中可以看出,相比不考虑残余应力的情况而言,存在残余应力时复合材料拉伸强度略有提高,这是由于基体热膨胀系数相对纤维较大,固化过程中会在界面处产生压应力,抵消了一部分拉伸载荷的影响;随着界面强度的提高,复合材料拉伸强度随之提高,但当界面强度接近基体强度后,界面强度的提高对复合材料拉伸强度的影响随之减弱。

图5 不同界面强度下横向拉伸应力-应变关系
图6中给出了界面强度为50MPa时复合材料的损伤演化过程。由图中可以看出当界面强度低于基体强度时,纤维/基体之间的界面先于基体发生破坏,在基体达到拉伸强度之前便发生了界面脱粘,原有界面变成了自由表面,内部应变能得到释放。随着界面损伤的积累,引起基体破坏,并最终导致材料整体失效,最终断裂形态与图6(c)的实验结果相似。当复合材料界面强度高于基体强度(即界面强度为100MPa)时损伤演化过程为:裂纹首先在基体中产生,随着损伤积累逐渐扩展到界面处,并最终引起断裂破坏。

图6 横向拉伸断裂仿真与实验结果[18]对比 (a)初始损伤;(b)最终断裂;(c)实验结果
3.2 压缩载荷
图7中给出了不同界面强度下复合材料横向压缩的应力-应变曲线,可以看出,界面强度相同时,由于界面处残余压应力的影响,使得复合材料横向压缩强度略有降低。
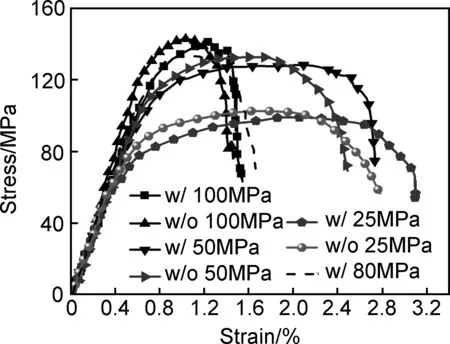
图7 不同界面强度下横向压缩断裂计算结果
从图7中可以看出复合材料横向压缩失效之前都表现出明显的非线性行为,这是由于在压缩载荷作用下,首先发生界面脱粘,随后出现基体裂纹,最终导致材料发生整体破坏。横向拉伸载荷作用下引起界面脱粘的是基体与纤维间的法向应力,而压缩载荷作用下界面脱粘是切向应力引起的。随着界面强度的提高,复合材料压缩断裂强度也随之增高,当界面强度从25MPa上升到50MPa时,复合材料压缩断裂强度提高了约22%,而随着界面强度的进一步提高,断裂强度提高则不明显,这是由于当界面强度增大到一定程度时,压缩时首先出现基体破坏,随着损伤积累才出现界面破坏,材料的性能主要由基体力学性能决定。标准界面下复合材料断裂角度如图8所示,与实验观察到的角度较为一致[19]。
3.3 剪切载荷
不同界面强度情况下,复合材料剪切性能的变化规律与压缩变化规律相似。由图9中可以看出残余应力对复合材料剪切性能影响不大。复合材料在剪切载荷作用下,法向应力与切向应力的综合作用导致部分界面早于基体发生失效。随着载荷的继续增加,界面损伤不再扩展,基体开始进入损伤阶段。当界面强度明显低于基体强度时,较弱的界面强度脱粘导致纤维与基体形成过多的既有表面而造成缺少足够的相互约束以维持整个单胞的剪切变形。因此,在线性段过后,随着加载的继续,平均应力有段较长的平缓上升过程。

图8 横向压缩断裂仿真与实验结果[19]对比 (a)初始损伤;(b)最终断裂;(c)实验结果
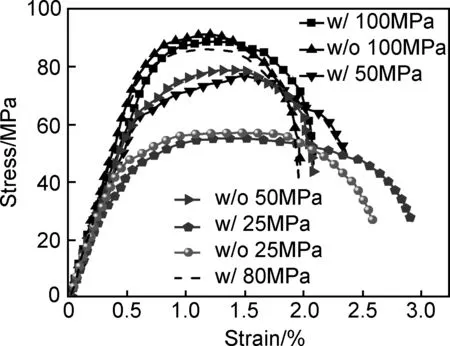
图9 不同界面强度下横向压缩断裂计算结果
4 结论
(1)建立了具有随机纤维分布的周期性代表单胞模型,通过摩尔-库仑塑性模型与Ductile damage失效准则结合模拟基体损伤演化过程,并将固化过程中的残余应力考虑在内,实现了复合材料横向模量、强度等力学参数的预测。
(2)将仿真结果与实验数据对比表明:复合材料横向模量误差在7%以内,横向压缩和剪切强度误差在8%以内,拉伸强度为11.2%,精度满足工程应用需求。
(3)固化过程中产生的残余应力导致复合材料横向拉伸强度略有提高,压缩强度略有降低,对剪切强度的影响不大。
(4)当界面强度低于基体强度时,复合材料横向强度由界面强度决定,随着界面强度的提高,复合材料横向强度有明显提高;当界面强度高于基体强度时,复合材料横向强度主要由基体性能决定,界面强度的变化影响不大。
[1] 杜善义,王彪. 复合材料细观力学[M]. 北京: 科学出版社, 1998.
DU S Y,WANG B. Micromechanics of Composite [M].Beijing:Science Press China,1988.
[2] GONZALEZ C, LLORCA J. Mechanical behavior of unidirectional fiber-reinforced polymers under transverse compression: microscopic mechanisms and modeling[J]. Composites Science and Technology, 2007,67(13):2795-2806.
[3] VAUGHAN T J, McCARTHY C T. A combined experimental-numerical approach for generating statistically equivalent fibre distributions for high strength laminated composite materials [J]. Composites Science and Technology,2010,70(2): 291-297.
[4] VAUGHAN T J, McCARTHY C T. Micromechanical modeling of the transverse damage behaviour in fibre reinforced composites [J]. Composites Science and Technology,2011,71(3):388-396.
[5] LU Z X, WANG C Y, XIA B, et al. Effect of interfacial properties on the uniaxial tensile behavior of three-dimensional braided composites [J]. Computational Materials Science,2013, 79: 547-557.
[6] YANG L, YAN Y, LIU Y J, et al. Microscopic failure mechanisms of fiber-reinforced polymer composites under transverse tension and compression[J]. Composites Science and Technology,2012,72(15):1818-1825.
[7] 雷友峰, 魏德明, 高德平. 细观力学有限元法预测复合材料宏观有效性能模量[J]. 燃气涡轮实验与研究, 2003, 16(3):11-15.
LEI Y F, WEI D M, GAO D P. Predicting macroscopic effective elastic moduli of composites by micromechanics FEM [J] . Gas Turbine Experiment and Research, 2003, 16(3): 11-15.
[8] 王兆清, 张景涛, 李淑萍. 计算复合材料有效弹性模量的重心有限元方法[J].复合材料学报,2007, 24(6): 173-179.
WANG Z Q, ZHANG J T, LI S P. Barycentric finite element method for predicting the effective elastic moduli of composite materials [J]. Acta Materiae Compositae Sinica, 2007, 24(6): 173-179.
[9] 徐强,卢子兴. 纤维排列方式对单向复合材料横向拉伸强度的影响[C]//中国力学大会2011暨钱学森诞辰100周年纪念大会论文集,哈尔滨: 中国力学学会, 2011: 1-10.
XU Q, LU Z X. Effects of fiber distributions on the transverse properties of unidirectional composites[C]//CCTAM2011, Harbin: CSTAM, 2011: 1-10.
[10] HOJO M, MIZUNO M, HOBBIEBRUNKEN T, et al. Effect of fiber array irregularities on microscopic interfacial normal stress states of transversely loaded UD-CFRP from viewpoint of failure initiation[J]. Compos Sci Technol, 2009, 69(11-12):1726-1734.
[11] MALIGNO A R, WARRIOR N A, LONG A C. Finite element investigations on the microstructure of fibre-reinforced composites[J]. Express Polym Lett, 2008, 2(9):665-676.
[12] MENETREY P H, WILLAM K J. Triaxial Failure criterion for concrete and its generalization[J]. ACI Structural Journal, 1995,92(6):311-318.
[13] SODEN P D, HINTON M J, KADDOUR A S. Lamina properties, lay-up configurations and loading conditions for a range of fiber-reinforced composite laminates [J]. Composites Science and Technology,1998,58(7):1011-1022.
[14] PITKETHLY M J,FAVRE J P,GAUR U,et al. A round robin programme on interfacial test methods[J]. Composites Science and Technology,1993,48(1-4):205-214.
[15] SEGURADO J, LLORCA J. A numerical approximation to the elastic properties of sphere-reinforced composites [J]. J Mech Phys Solids,2002,50(10):2107-2121.
[16] XIA Z H, ZHANG Y F, ELLYIN F. A unified periodical boundary conditions for representative volume elements of composites and applications [J]. International Journal of Solids and Structures, 2003, 40(8): 1907-1921.
[17] O’HIGGINS R M, McCARTHY C T, McCARTHY M A. Identification of damage and plasticity parameters for continuum damage mechanics modelling of carbon and glass fibre-reinforced composite materials[J]. Strain,2011,47(1):105-115.
[18] WANG X Q, ZHANG J F, WANG Z Q. Effects of interphase properties in unidirectional fiber reinforced composite materials[J]. Materials & Design, 2011, 32(6): 3486-3492.
[19] BUDIANSKY B, FLECK N A. Compressive failure of fiber composites[J]. Mech Phys Solids,1993,41(1):183-211.
--------------------●
Analysis of Composite Transverse Mechanical Properties Based on Micromechanical Finite Element Method
LIU Wan-lei,CHANG Xin-long,ZHANG Xiao-jun,ZHANG Lei
(The Second Artillery Engineering University, Xi’an 710025, China)
Transverse fracture often occurs early in the loading history and is one of the key issues limiting the composite structural design. However, the mechanical behavior under transverse loading can not be represented by traditional micromechanical model which does not consider the influence of constituent properties, fiber volume fraction and fiber distribution. A new computational micromechanics finite element method, which the microstructure was idealized as a random dispersion of parallel fibers embedded in the polymeric matrix using improved random sequence absorption algorithm, was presented. The plasticity of matrix and interface decohesion of the composite were included in this model and the residual stress caused by the cooling of composite after the curing process was also taken into consideration. The transverse tension, compression and shear of composite were analyzed by the micromechanical finite element method. Compared with the experiment results, the prediction errors of transverse module were less than 7%, and the transverse compression strength and shear strength were less than 8%. The results demonstrate that the method proposed here can be used to predict the composite transverse behavior.
composite;micromechanical finite element;residual stress;interface strength;transverse mechanical property
10.11868/j.issn.1001-4381.2016.11.018
TB33
A
1001-4381(2016)11-0107-07
国家自然科学基金项目(11302249)
2015-05-25;
2016-07-27
常新龙(1965-),男,教授,博士生导师,博士,主要从事失效物理与可靠性方面的研究工作,联系地址:陕西省西安灞桥区洪庆镇同心路2号3602分队(710025),E-mail:xinlongch@sina.com

